Dimensional Analysis
As you work on problems that involve numbers with units of measurement, it is convenient to consider the units (or dimensions) as factors. For example, you might want to change 0.002 kilometer to millimeters. You can always multiply by 1 without changing a value, so to convert between units you can multiply by a unit fraction. A unit fraction’s value is 1 because its numerator and denominator are equivalent. Some unit fractions are shown here.
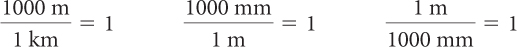
To convert from kilometers to millimeters, use the unit fraction with meters in the numerator and the equivalent kilometers in the denominator and a unit fraction with millimeters in the numerator and equivalent meters in the denominator.
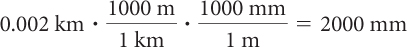
You can see that the unit fractions have been chosen so that most of the units cancel out. The answer is then in millimeters as they are the only remaining units.
Dimensional analysis is also helpful when you need to convert between two different systems of measurement. For example, 1 inch is equivalent to 2.54 centimeters. To convert from centimeters to inches, use the unit fraction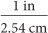 
. To convert from inches to centimeters, use the unit fraction 
.
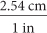Example 1
Calculating Volume
What is the volume of a box 1 5cm by 10 cm by 5.12 in.?
Solution
The volume is the product of the three dimensions, but you need to include a factor to convert the inches to centimeters.
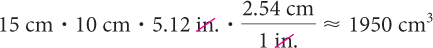
If the problem specified the answer in cubic inches, you would have used this product.
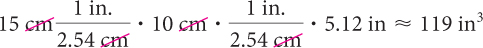
A-17
Example 2
Speed
A radio-controlled car travels 30 feet across the room in 1.6 seconds. How fast is it traveling in miles per hour?
Solution
From the information, the rate of the car is 
. Multiply by unit fractions such as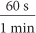 
to go from seconds to minutes to hours and from feet to miles. These fractions are chosen so that the final units are miles per hour.
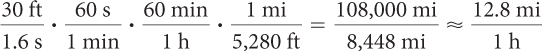
or 12.8 miles per hour
Practice Exercises
Show how you would use dimensional analysis to convert 6 cm/s to km/h.
Use dimensional analysis to change
50 meters per second to kilometers per hour
0.02 5day to seconds
the speed 60 miles per hour to kilometers per hour. (1609 meters = 1 mile)
The equation for the universal gas law is PV = nRT. Suppose the pressure P is in pascals (Pa), the volume V is in cubic meters (m3), the amount of substance n is in moles (mol), and the temperature T is in kelvins (K). What must be the units of the universal gas law constant R?
Answers
1. 
|
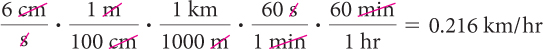
| 2a. 180 km/h |
| 2b. 2160 |
| 2c. 97 km/h |
3. 
|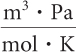