LESSON 51: Having A Meltdown: Density of Liquids and Solids
267
THINK ABOUT IT
Much of the country depends on snowfall for the year’s water supply. The mountains get many feet of snow every winter, and this snow eventually melts and travels from creek to stream to river to reservoir. Scientists measure the snowpack, or the total amount of snow that has accumulated on the ground, to predict the amount of water that will be available for consumption the rest of the year. But is the amount of water in a foot of snow in the mountains equal to the amount in a foot of rainfall?
How much water is present in equal volumes of snow and rain?
To answer this question, you will explore
Density and Phase
Converting Snowfall to Rainfall
The Density of Ice
Density and Phase
EXPLORING THE TOPIC
Density and Phase
Just as rainfall is measured in inches, snowfall can also be measured in inches. All you need is a ruler. However, scientists who study water distribution are more interested in how much liquid water the snow represents.
When snow melts, its volume decreases. However, its mass is still the same. This is because the same water molecules are present in the frozen snow and in the melted snow.
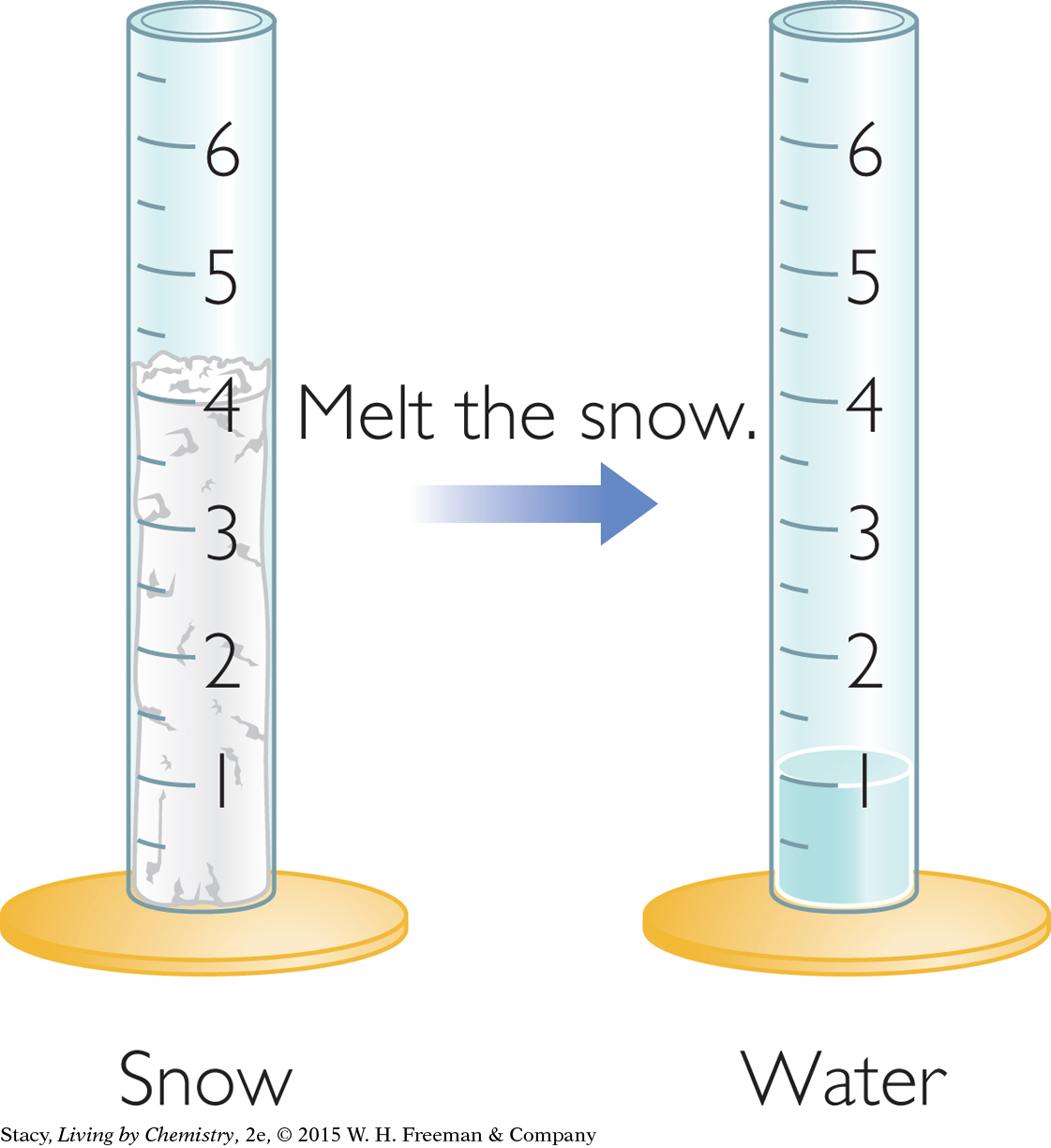
If the volume of the sample changes but its mass stays the same, then mathematically, the density of the sample has to change. The density of snow must be lower than the density of water.
Recall that density is the mass per unit volume.
Unlike water, snow has a wide range of densities. Snow can be fluffy or packed. So, the volume of liquid water contained in any snow sample depends on the density of the snow being considered.
268
MASS AND VOLUME ARE PROPORTIONAL
ENVIRONMENTAL CONNECTION
ENVIRONMENTAL
CONNECTION
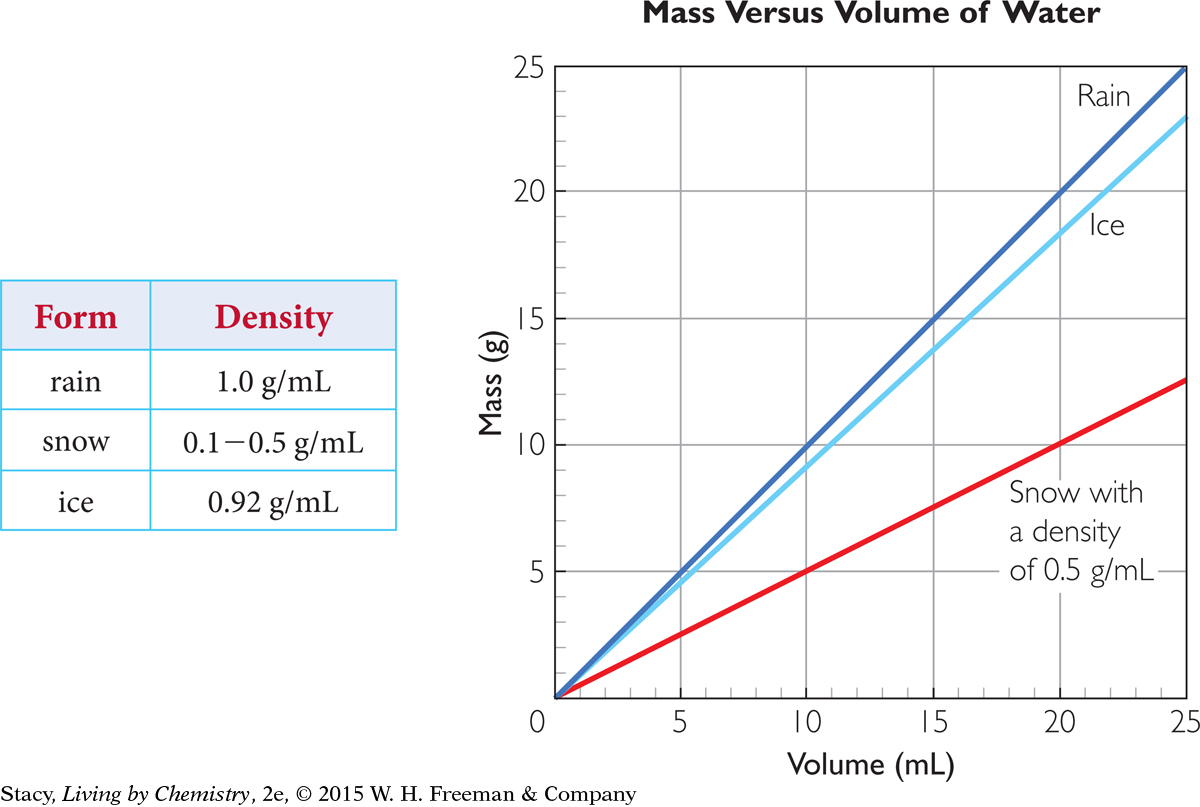
Snowpack density can vary from about 0.1 g/mL to 0.5 g/mL, depending on conditions. Dry, fluffy snow is less dense than wet, slushy snow, and therefore easier to shovel.

The equation for density relates mass and volume.
As long as the density of the substance doesn’t change, its mass and volume are proportional. The proportionality constant here is the density, D.
m = DV
Because mass and volume are proportional to each other for a specific substance, the data points lie on a straight line that goes through the origin. Examine the graphs of mass versus volume for rain, snow, and ice. How does the slope of the line relate to the density?
Big Idea
Big Idea
Matter changes density when it changes phase.
Converting Snowfall to Rainfall
Converting Snowfall to Rainfall
CALCULATING THE DENSITY OF SNOW

Florence Low/California Department of Water Resources
|

Philippe Psaila/Science Photo Library
|
One way to determine the volume of water in a snowpack is to melt the snow. But melting a large amount of snow is inconvenient.
Another way to study the water volume of the snowpack is to determine the density of the snow and calculate the volume of liquid water it represents. When new snow has fallen in the mountains, hydrologists take samples of the snow with a large aluminum tube. They push the empty tube all the way down into the snow. Then they weigh the tube with the snow still inside. The density of the snow is the mass divided by the volume.
269
SPORTS CONNECTION
SPORTS
CONNECTION
Skiers and snowboarders enjoy fresh “powder.” This is the term for untouched, freshly fallen snow with a particularly low density. Powder is perfect for landing on because it forms a natural cushion. This means that it does not hurt as much when you land on it compared with snow that is compacted.

Example
Volume of Water from Snow Melt
Suppose you have a volume of 20 mL of snow with a density of 0.25 g/mL. What volume of liquid water do you get when you melt this amount of snow?
Solution
When the snow melts, its mass will not change. Use the density equation to convert between mass and volume.
| Use the volume and density of snow to find its mass. | msnow = Dsnow Vsnow= (0.25 g/mL) · (20 mL) = 5 g |
| The mass of snow is equal to the mass of water. | msnow = mwater = 5 g |
| Rearrange the density equation to find the volume of water. |
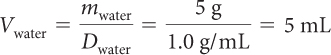
|
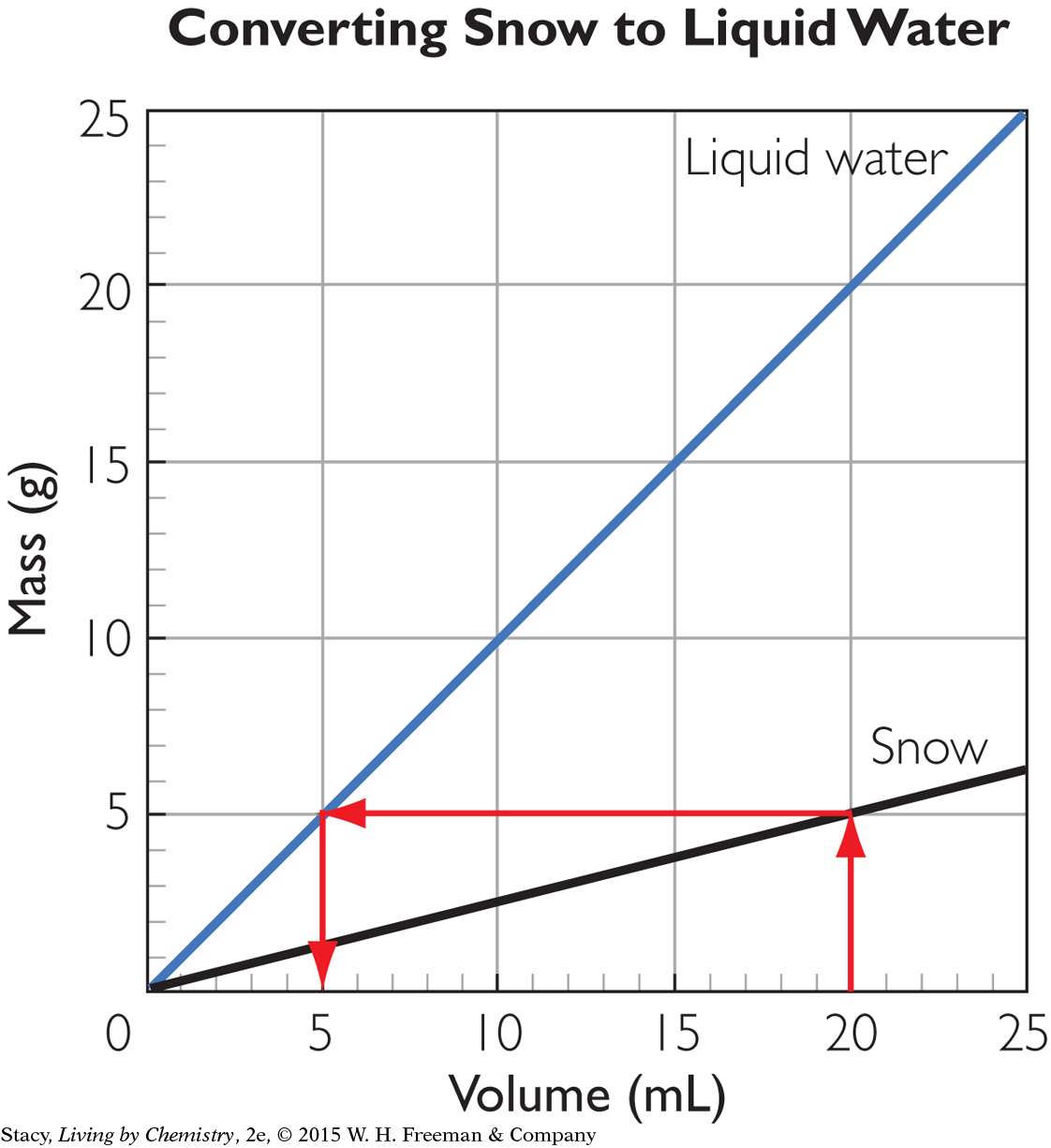
When 20 mL of snow with a density of 0.25 g/mL melts, you get 5 mL of water.
You can also solve this problem using a graph. The graph here shows mass versus volume for liquid water, as well as snow with a density of 0.25 g/mL.
The Density of Ice
The Density of Ice
270
ENVIRONMENTAL CONNECTION
ENVIRONMENTAL
CONNECTION
Most substances contract when they freeze, becoming denser. Water is unique in that it expands when it freezes, becoming less dense. This is why ice floats in water. Otherwise, icebergs would sink!

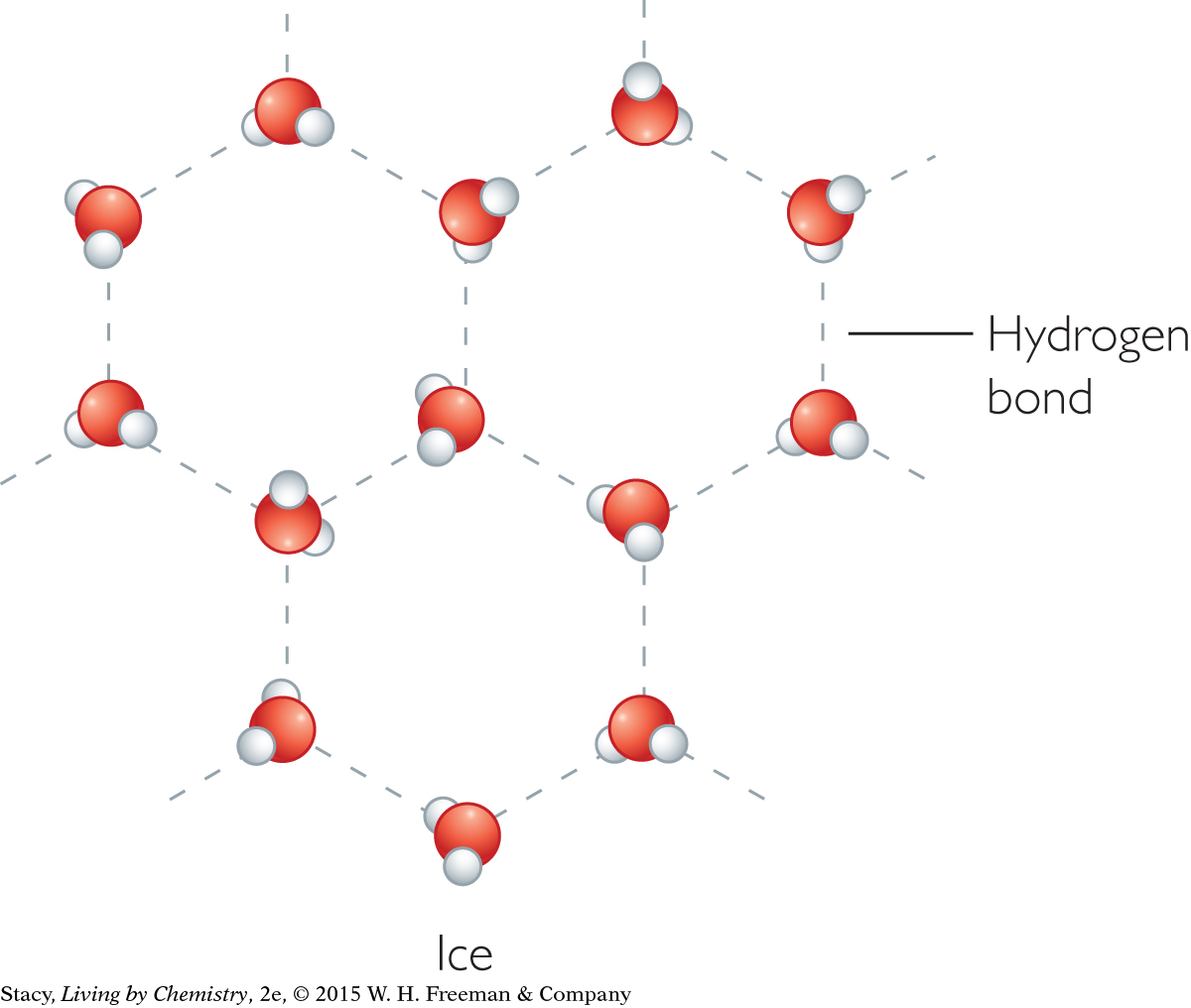
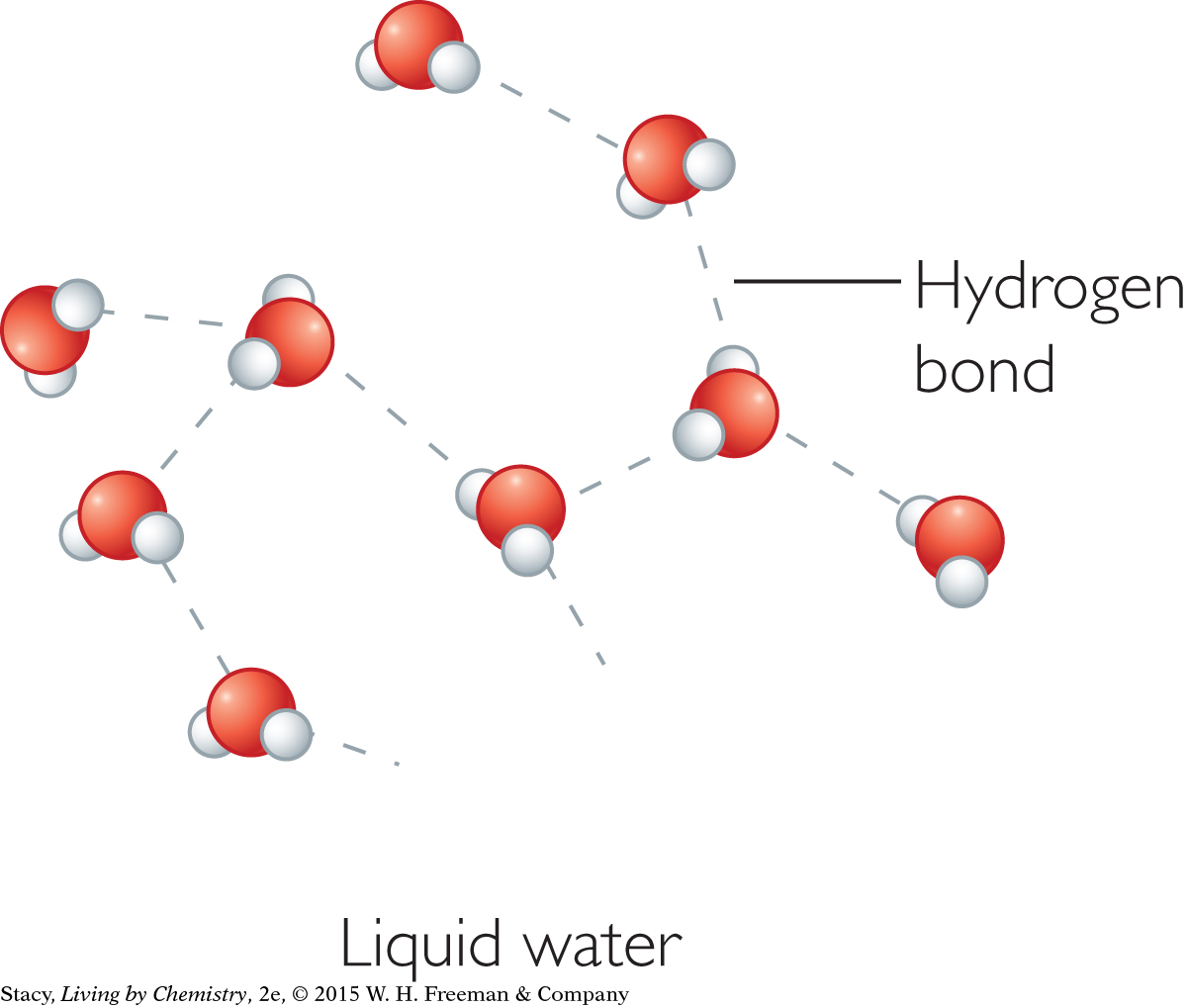
The density of ice is 0.92 g/mL. It is less than the density of liquid water, which is 1.0 g/mL. Because water becomes less dense when it freezes, its volume increases. This unique property of water is due to a special kind of intermolecular force called hydrogen bonding. In both liquid and solid water, the hydrogen atoms in one water molecule attract the highly electronegative oxygen atoms in another. When water freezes, the molecular motion slows down and the molecules lock into a hexagonal structure due to hydrogen bonding.
|
|
LESSON SUMMARY
LESSON SUMMARY
How much water is present in equal volumes of snow and rain?
The density of snow is less than the density of liquid water. You can use mathematical equations or graphs to convert the volume of snow to the volume of liquid water. To use graphs, you plot two lines of mass versus volume, one for snow and another for liquid water. The slope of each line is the density of that substance. To use mathematical equations, you have to know the density of the snow and the density of liquid water.
Exercises
Reading Questions
Explain how to use mathematical equations to convert the volume of snow in a snowpack to the volume of water in the snowpack.
Explain how to use graphs to convert the volume of snow in a snowpack to the volume of water in the snowpack.
Reason and Apply
How are snow and ice different?
When ice melts, will the liquid water occupy more or less volume than the ice? Explain your thinking.
Suppose that you melt 24 mL of ice. What is the volume of liquid water that results?
271
Which has more water for equal volumes of snow: snow with a density of 0.5 g/mL or snow with a density of 0.25 g/mL? Explain your thinking.
Suppose you have a box with a volume of 17.5 mL.
If you fill this box with ice, what mass of ice do you have? (The density of ice is 0.92 g/mL.)
If you fill this box with liquid water, what mass of liquid water do you have? (The density of liquid water is 1.0 g/mL.)
Suppose that you have a box that is full and contains 500 grams of a substance.
What is the volume of the box if the substance inside is corn oil? (The density of corn oil is 0.92 g/mL.)
What is the volume of the box if the substance inside is lead? (The density of lead is 11.35 g/mL.)
Lead, Pb, is more dense than iron, Fe.
Which occupies a larger volume: 4.3 g of Pb or 4.3 g of Fe? Explain your thinking.
Which has a larger mass: 2.6 mL of Pb or 2.6 mL of Fe? Explain your thinking.