LESSON 65: Take A Breath: Ideal Gas Law
335
THINK ABOUT IT
Climbing Mount Everest is extremely difficult without bringing along a tank of oxygen to help you breathe. As you climb higher and higher, the air pressure gets lower and lower. At 29,000 ft, on top of Mount Everest, the air pressure is only 0.33 atm. You might wonder how many oxygen molecules are available at this pressure.
How can you calculate the number of moles of a gas if you know P, V, and T ?
To begin to answer this question, you will explore
Pressure, Volume, Temperature, and Number
The Ideal Gas Law
Pressure, Volume, Temperature, and Number
EXPLORING THE TOPIC
Pressure, Volume, Temperature, and Number
Four variables describe gas samples: pressure, volume, temperature, and number of moles of atoms or molecules. Any two variables can be related to each other mathematically if the other two are kept the same. You might begin to wonder if you can relate all four variables in a single equation. The combined gas law relates three of the variables: pressure, volume, and temperature.
So far you’ve learned that at STP, there is 1.0 mol of gas molecules in a volume of 22.4 liters for any gas sample.
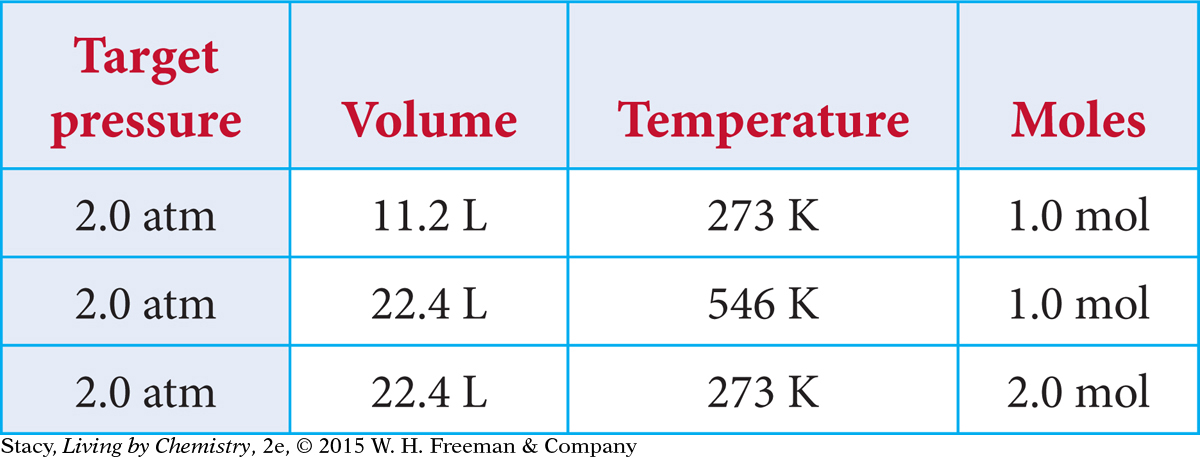
INCREASING THE PRESSURE
Suppose you want to adjust this sample of gas so that it has a pressure of 2.0 atm. In what ways can you accomplish this?
You can change the pressure to 2.0 atm in different ways.
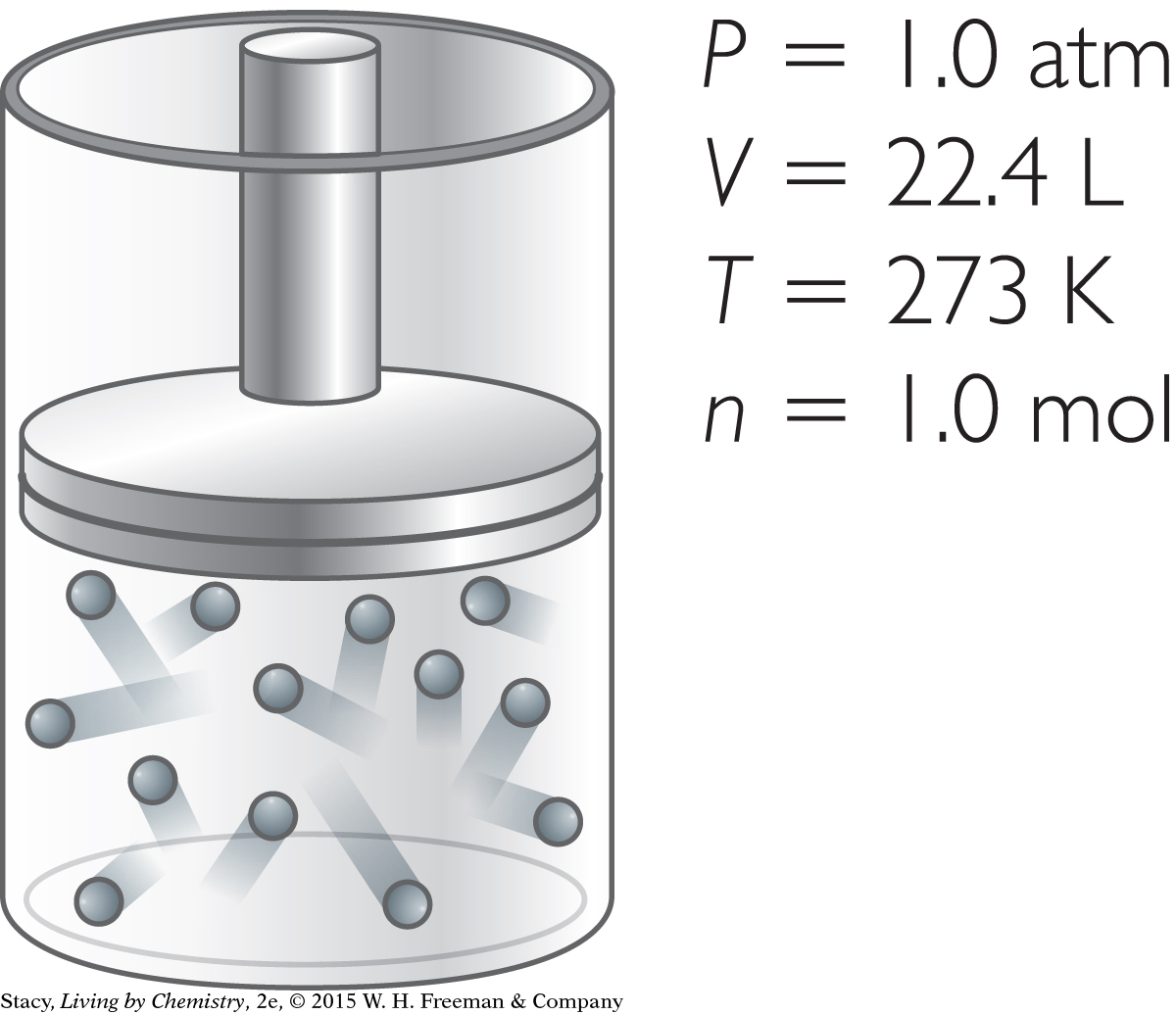
Original gas sample
|
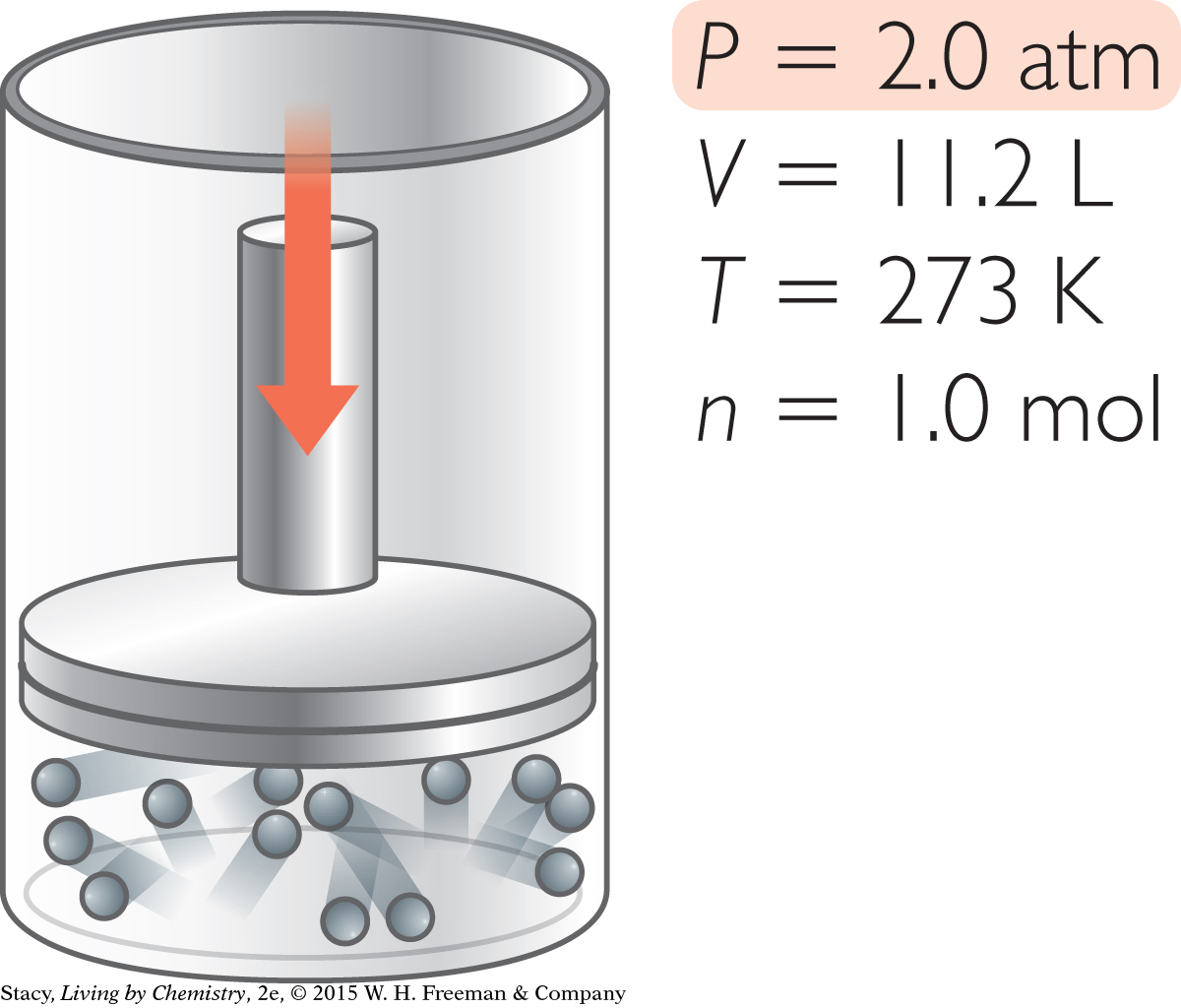
Decrease V. Squeeze the gas at 273 K into a volume of 11.2 L.
|
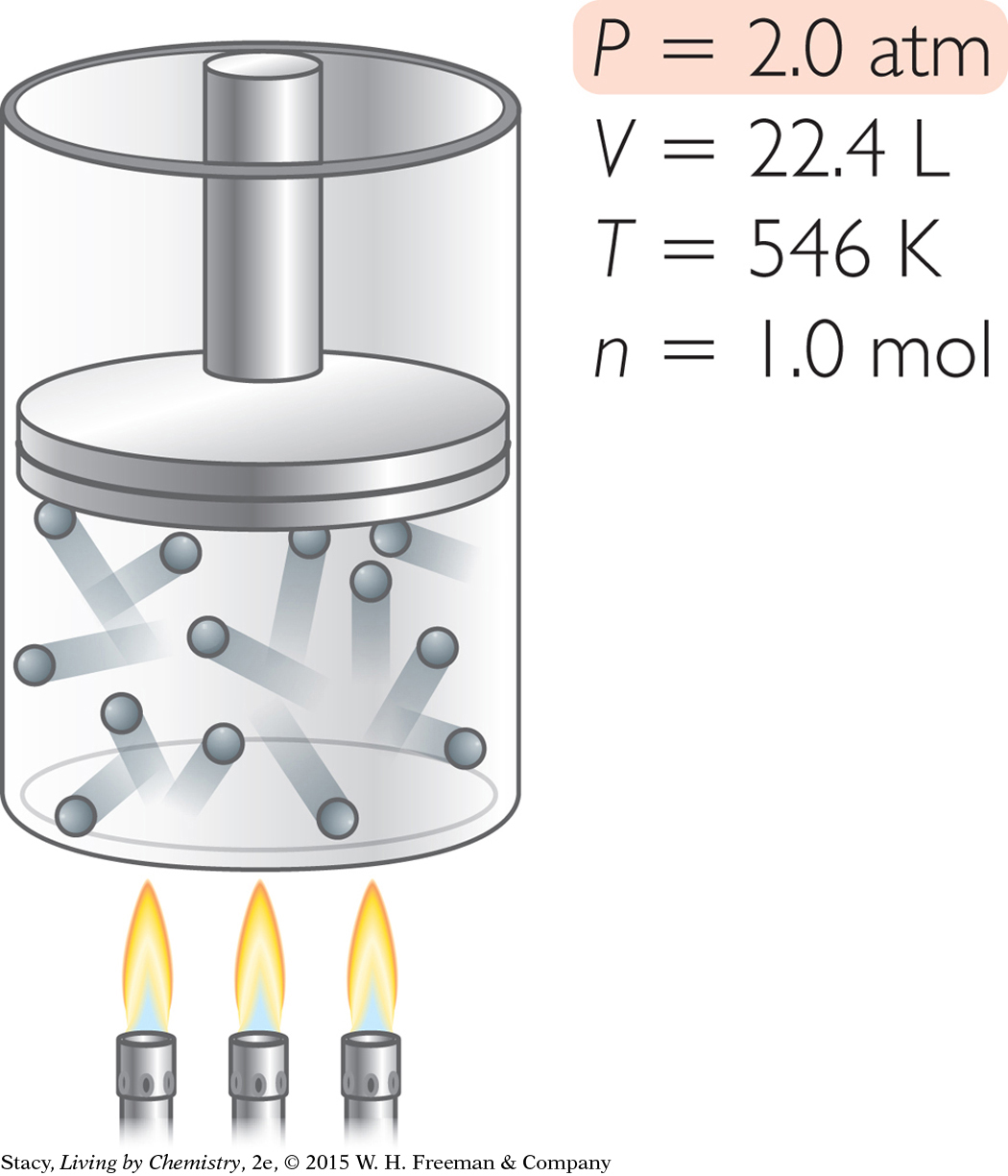
Increase T without changing V. Heat the gas in 22.4 L to a temperature of 546 K.
|
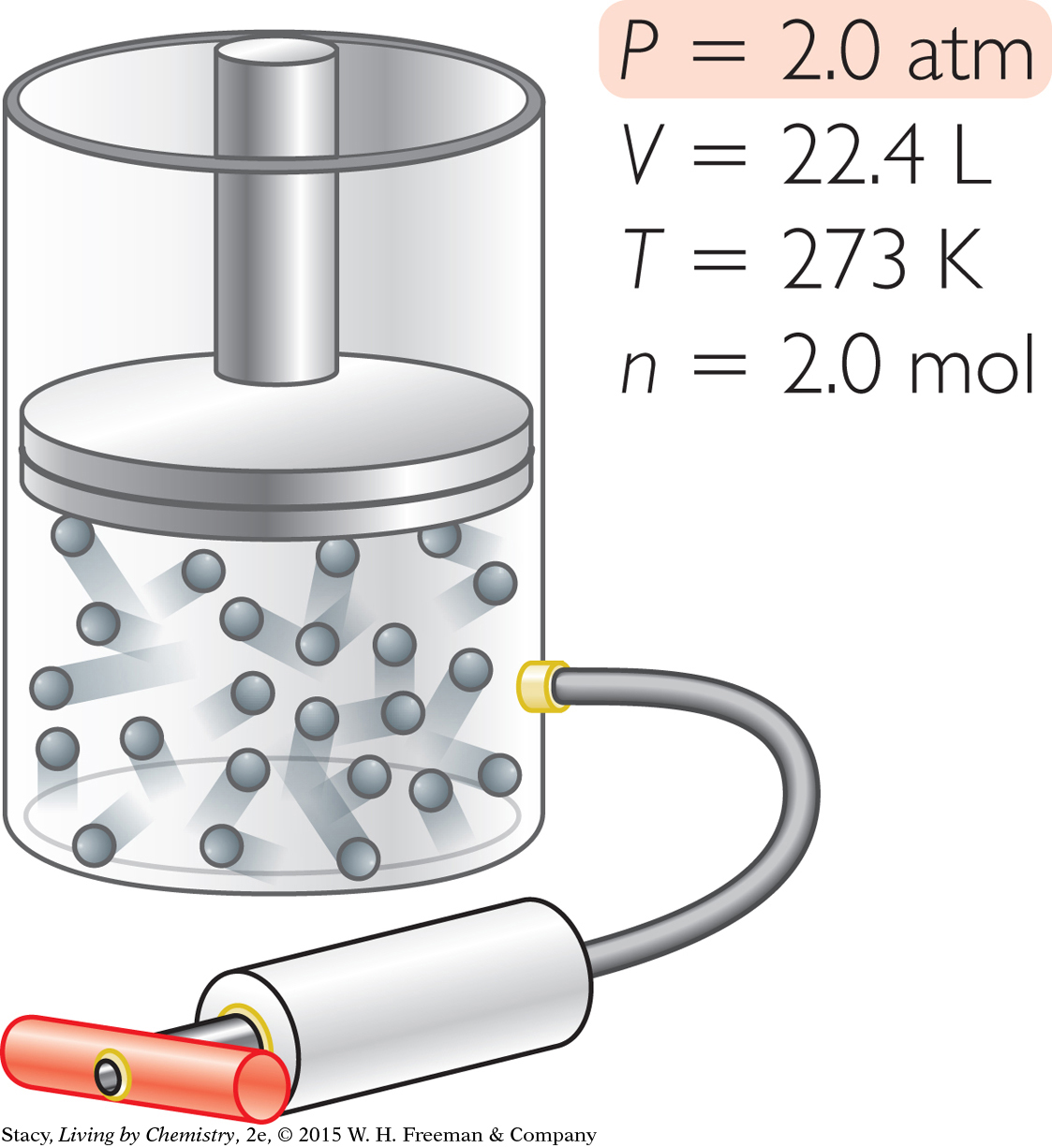
Increase n without changing V. Add 1.0 mol of gas molecules to the container at 273 K at a volume of 22.4 L.
|
336
So while the pressure is the same in each case, you can see how the other variables have changed.
INCREASING THE VOLUME
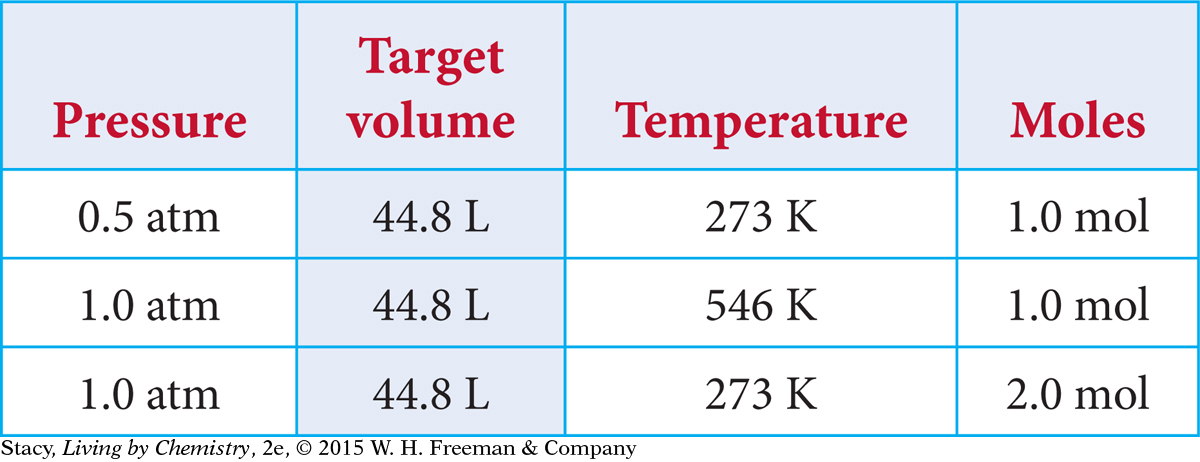
Suppose you want to adjust the original sample of gas so that it has a volume of 44.8 L. How can you accomplish this?
You can produce a sample of gas with a volume of 44.8 L in several ways.
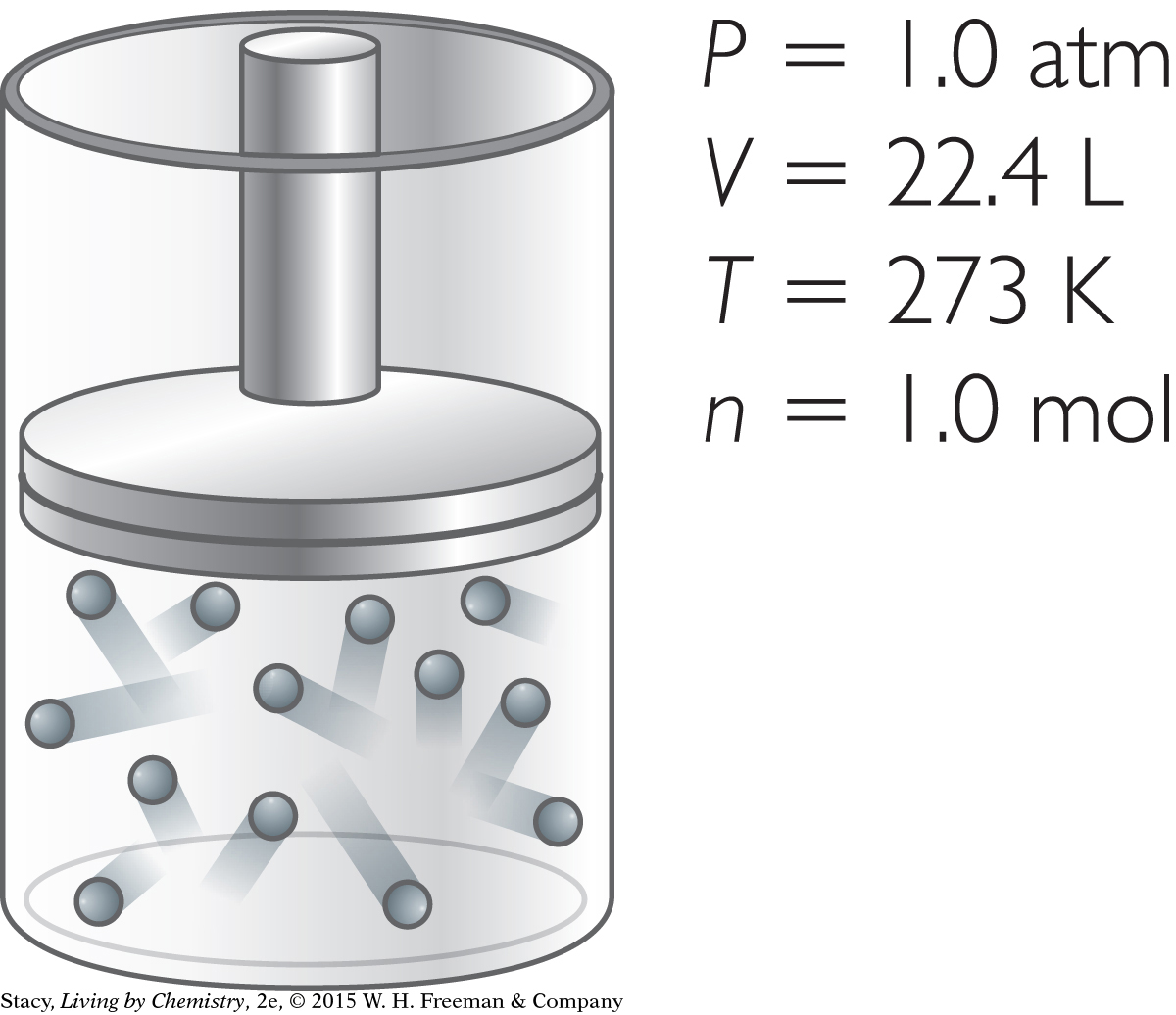
Original gas sample.
|
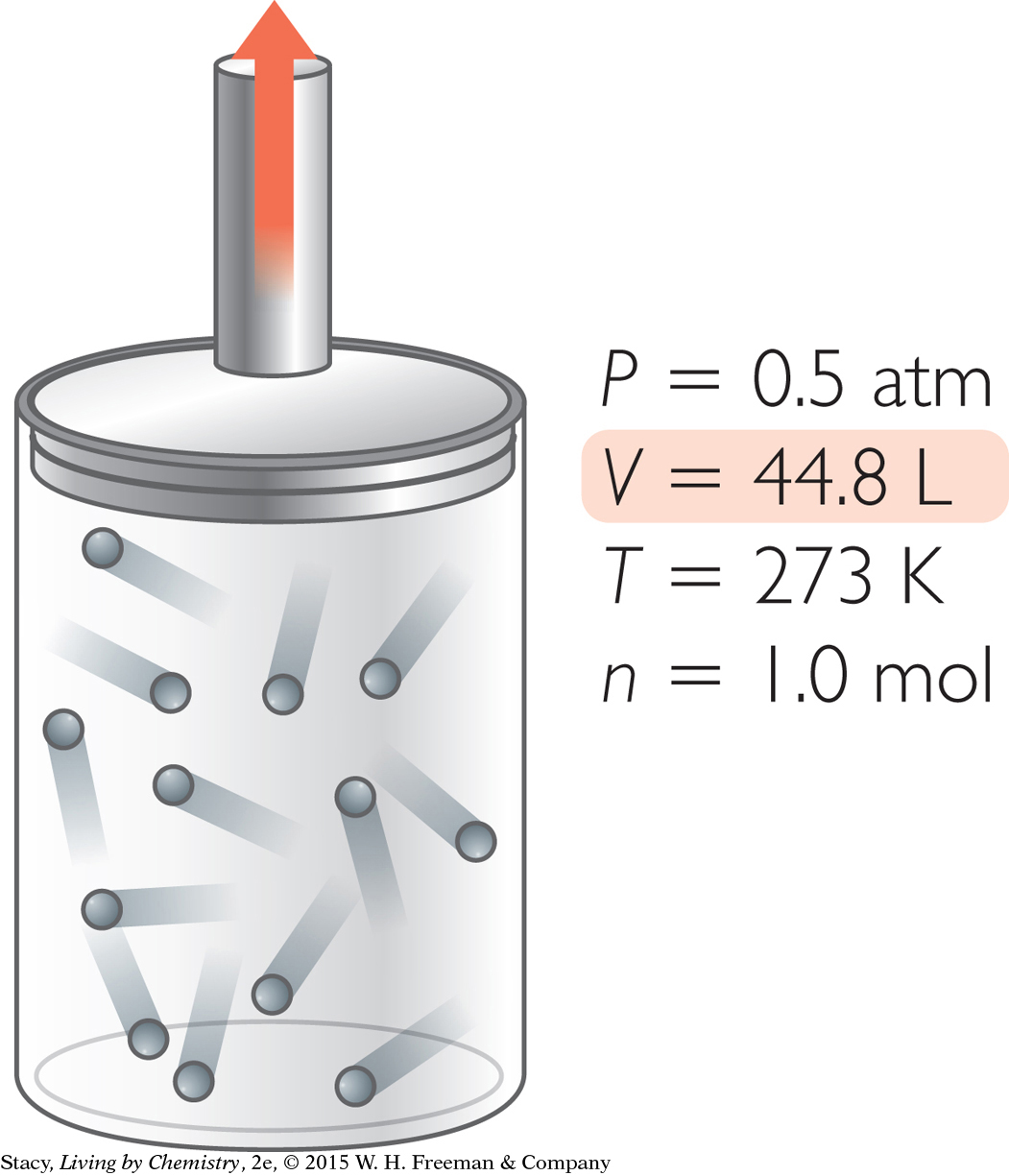
Increase V. Expand 1.0 mol of gas molecules at 273 K until the pressure is 0.5 atm.
|
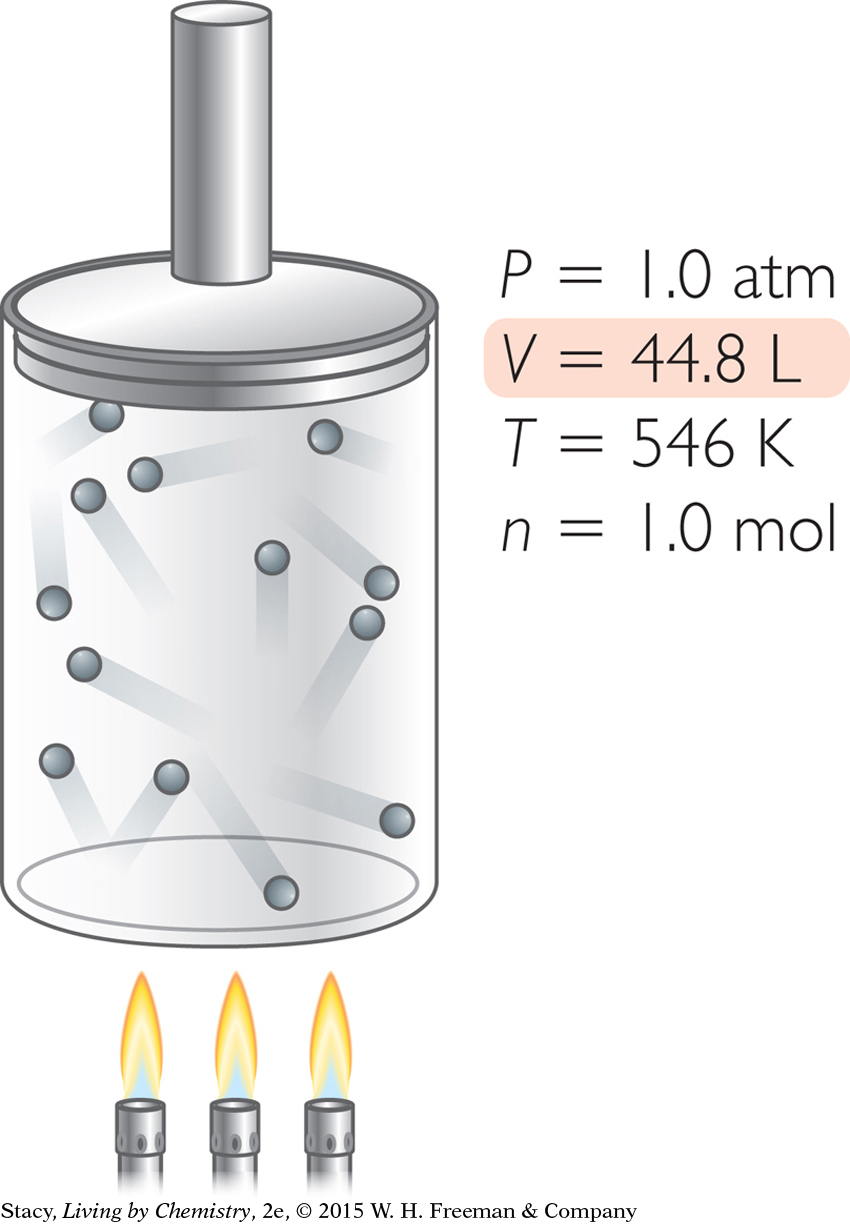
Increase T. Heat 1.0 mol of gas molecules at 1.0 atm to a temperature of 546 K.
|
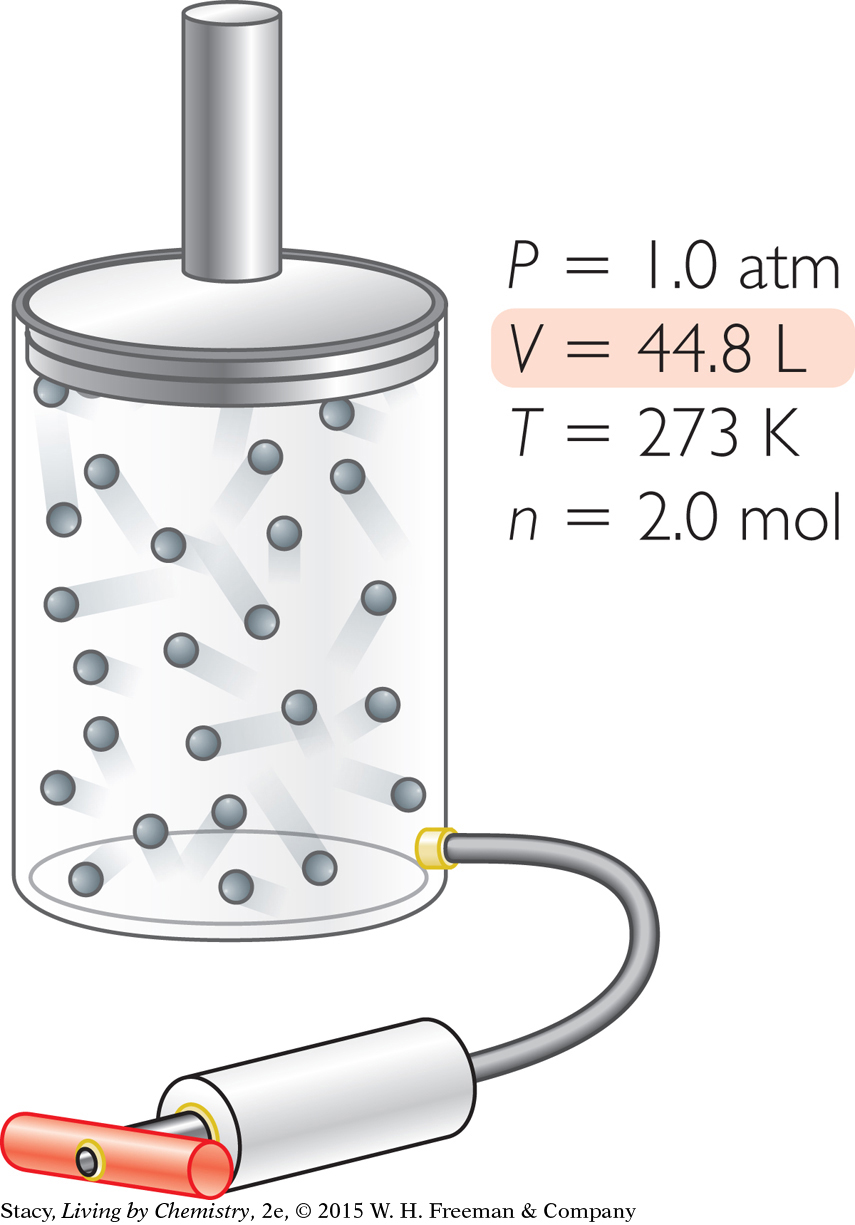
Increase n. Add 1.0 mol of gas molecules to the container at STP, to arrive at 2.0 total moles.
|
It is apparent that these variables are mathematically related. In fact, if you combine the equation for the combined gas law with the relationship described by Avogadro’s law, the result is a mathematical relationship known as the ideal gas law.
The Ideal Gas Law
The Ideal Gas Law
HEALTH CONNECTION
HEALTH
CONNECTION
Altitude sickness occurs at high altitudes when people cannot get enough oxygen from the air. It causes headaches, dizziness, lethargy, nausea, and lack of appetite. It can be quite dangerous for mountain climbers.

337
The ideal gas law relates the pressure, volume, temperature, and number of moles for a gas sample.
Ideal Gas Law
The product of the pressure, P, and volume, V, of a gas is proportional to the product of the number of moles, n, and the temperature, T.
PV = nRT
The two products are related by the constant, R.

The universal gas constant, R, is the same for all gases.
Because R has units of L · atm/mol · K, you can use this value of R only if volume is measured in liters, pressure in atmospheres, temperature in kelvins, and number of gas molecules in moles. When these units are used, R is always equal to 0.082 L · atm/mol · K.
If you know three of the four variables for any gas sample, you can use the ideal gas law to calculate the fourth variable. This is most useful in determining the moles of gas molecules in a gas sample because the pressure, volume, and temperature can be easily measured.
Example
Moles of Air on Mount Everest
How many moles of air are in a 0.5 L breath on top of Mount Everest? The pressure is 0.33 atm and the temperature is 254 K.
Solution
The ideal gas law relates all these quantities. Insert the values for P, V, T, and R into the equation and solve for n.
PV = nRT
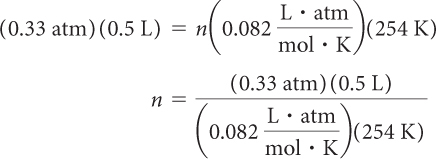
n = 0.008 mol of air
So there is only 0.008 mol of air molecules in a 0.5 L breath of air atop Mount Everest.
338
LESSON SUMMARY
LESSON SUMMARY
How can you calculate the number of moles of a gas if you know P, V, and T ?
KEY TERMS
ideal gas law
universal gas constant, R
Any sample of gas can be described by four variables: pressure, volume, temperature, and moles. The ideal gas law relates these four variables to each other mathematically: PV = nRT, where R is the universal gas constant. The value of R is 0.082 L · atm/mol · K for all gas samples if units of atmospheres, liters, moles, and kelvins are used. If you know three of the four variables for any gas sample, you can use the ideal gas law to calculate the fourth variable.
Exercises
Reading Questions
What is the ideal gas law?
Describe when you might want to use the ideal gas law.
Reason and Apply
How many moles of hydrogen, H2, gas are contained in a volume of 2 L at 280 K and 1.5 atm?
What volume would 1.5 mol of nitrogen, N2, gas occupy at standard temperature and pressure?
Find the pressure of 3.40 mol of gas if the gas temperature is 40.0 ºC and the gas volume is 22.4 L.
How many moles of helium, He, gas are contained in a 10,000 L weather balloon at 1 atm and 10 ºC?
Suppose you have 1.0 mol of gas molecules in 22.4 L at STP. Describe three ways you can get a gas pressure of 0.50 atm.
Will the pressure of helium, He, gas be the same as the pressure of oxygen, O2, if you have 1 mol of each gas, each at a volume of 22.4 L and each at 273 K? Explain your thinking.