LESSON 81: Drop In: Molecular Views
413
THINK ABOUT IT
A tiny drop of a concentrated solution of hydrochloric acid, HCl(aq), will cause a severe burn if it comes in contact with your skin. In contrast, a larger volume of a more dilute HCl(aq) solution will cause only a minor skin irritation. How can a single drop of a solution be so powerful?
How can you use molarity to determine the moles of solute?
To answer this question, you will explore
Particle Views of Solutions
Molarity Calculations
Particle Views of Solutions
EXPLORING THE TOPIC
Particle Views of Solutions
When a toxin is dissolved in water, the amount of toxin you are exposed to depends on both the concentration of the solution and the volume of the solution. To better understand the relationship between solution concentration and solution volume, it is useful to explore solutions with the same volume but different concentrations, as well as solutions with the same concentration but different volumes.
SAME VOLUME, DIFFERENT CONCENTRATIONS
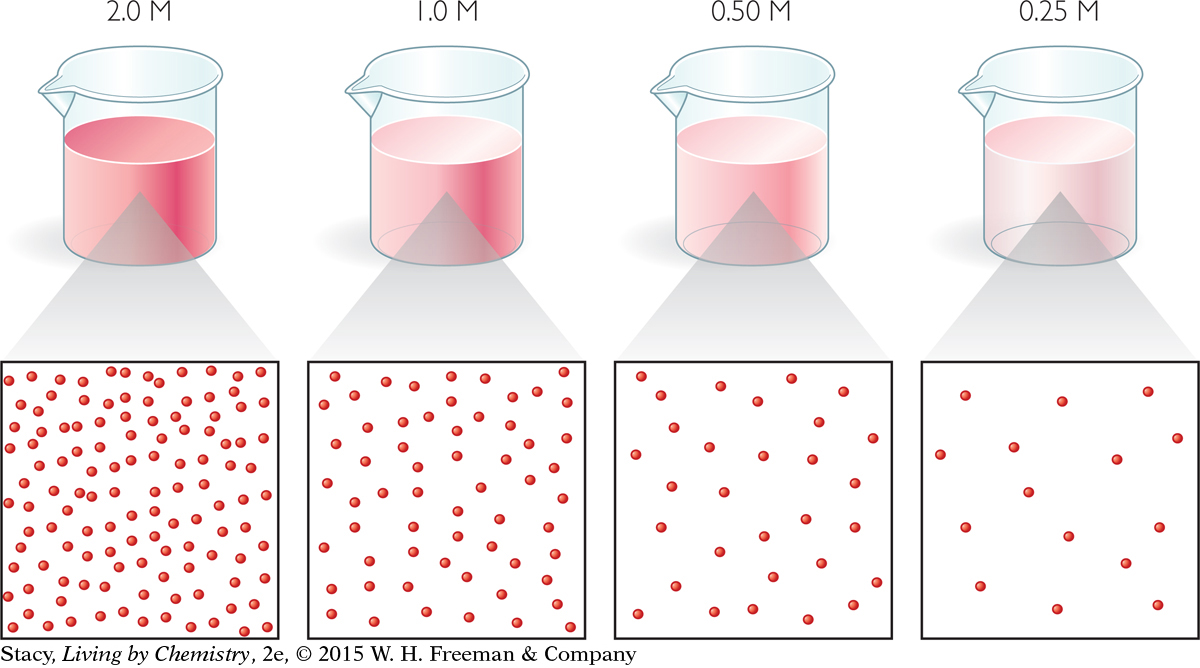
This illustration shows four solutions of red dye, as well as particle views of each. Each red dot represents a red dye molecule dissolved in water. Take a moment to compare the solutions and molecular views.
414
SPORTS CONNECTION
SPORTS
CONNECTION
Chlorine, found in hypochlorous acid, HOCl, is toxic to humans in high concentration. However, a tiny amount can be added to a swimming pool to make the water safe. The low concentration is deadly to bacteria and other microorganisms but not to humans—though it can irritate the eyes and skin.

Notice that each time the concentration is halved, there are half as many particles per unit of volume. So, as the solution concentration decreases, equal volumes of solution will contain fewer molecules.
The color of the red dye solution provides evidence to support this conclusion. When there are more dye molecules per unit of volume, the red color of the solution is more intense.
SAME CONCENTRATION, DIFFERENT VOLUMES
The particle views of the two solutions in the next illustration show what happens when you pour a portion of a solution into another container. Take a moment to compare the solutions and molecular views.
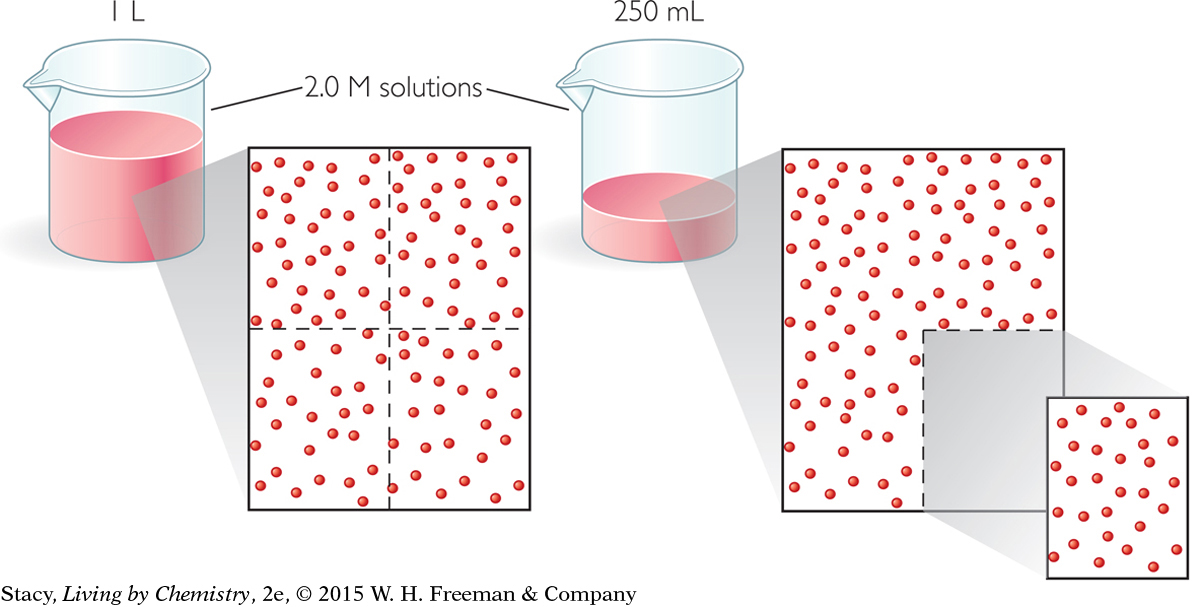
There are fewer total dye molecules when you pour a portion of the solution into the smaller container. However, the concentration of the solution has not changed. If you remove 250 mL from a 1 L solution, you have one quarter as many dye molecules. But because the concentration has not changed, the color of the red dye solution does not change.
Molarity Calculations
Molarity Calculations
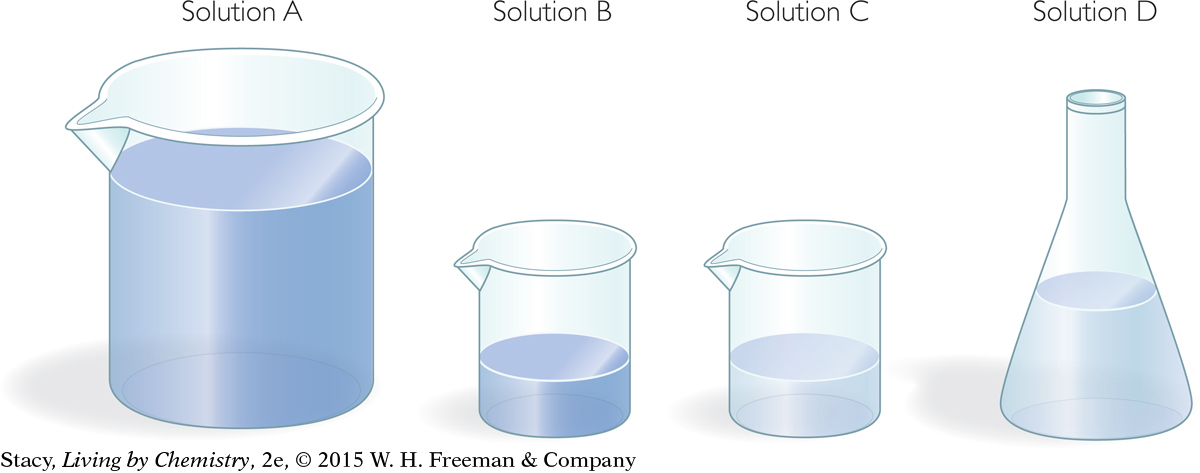
Consider the solutions below. Suppose the first two contain a concentrated solution of a toxin. The third and fourth contain a more dilute, or watered down, solution of the same toxin. Take a moment to try to put the solutions in order of most total moles of toxin to least total moles of toxin.
415
The relationship between moles of solute and volume of solution in liters is proportional. Recall that the molarity of a solution in moles/liter is the proportionality constant, k, for that solution. So, if you multiply the molarity by the volume in liters, you can determine the number of moles of solute.
moles of solute = k · volume of solution in liters
= 6.0 mol/L · 1.0 L = 6 mol Solution A
= 6.0 mol/L · 0.10 L = 0.60 mol Solution B
= 2.0 mol/L · 0.10 L = 0.40 mol Solution C
= 2.0 mol/L · 0.20 L = 0.20 mol Solution D
You can see that even though the volume of Solution B is smaller than the volume of Solution D, there are more moles of toxin dissolved in Solution B. This is because Solution B is more concentrated than Solution D.
A small drop of highly concentrated toxin may be worse for you than a large quantity of dilute toxin. For example, a 2 mL drop of 12 M HCl solution is much more toxic than 50 mL of 0.10 M HCl solution.
Big Idea
Big Idea
The concentration of a solution does not change with the size of the sample.
Example
Comparing Moles of Solute
Two solutions of a toxic substance are shown in the illustration.
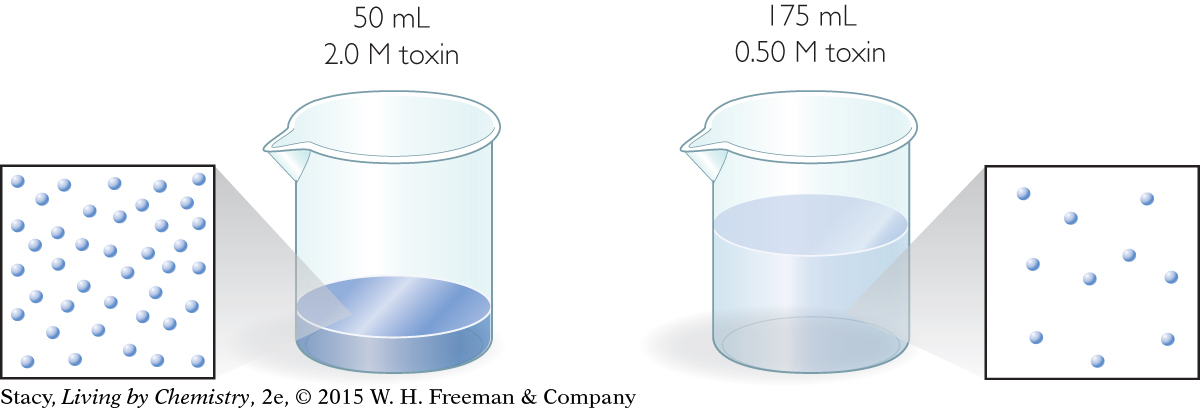
Which beaker contains the larger dose of the toxic substance?
Solution
Use the concentration of each solution to determine the moles of solute.
2.0 M solution: 2.0 mol/L · 0.050 L = 0.10 mol
0.50 M solution: 0.50 mol/L · 0.175 L = 0.0875 mol
So, the beaker on the left, the more concentrated solution, contains more moles of toxic substance.
416
HEALTH CONNECTION
HEALTH
CONNECTION
Fructose is a natural sugar found in fruits and vegetables. However, when it is highly concentrated, as it is in high-fructose corn syrup, it is difficult for your body to process. Too much of it can cause health problems.

Scientists also measure the concentration of substances in solution using parts per million (ppm) or parts per billion (ppb). When water is tested, the results are often reported in ppm. A level of 1 ppm means that there is 1 mg of a dissolved solute per liter of solution.
LESSON SUMMARY
LESSON SUMMARY
How can you use molarity to determine the moles of solute?
The concentration of a solution does not change with the size of the sample. This is because concentration is a measure of number density, or moles of particles per unit of volume, a property that does not change with sample size. However, a large sample of a solution will contain more total particles than a small sample of the same solution. The relationship between moles of particles in a solution and liters of solution is a proportional one. It is described by the formula, moles of solute = k · volume of solution, where k is the molarity of the solution. This equation can be used to calculate the exact number of moles in a sample of known concentration and volume.
Exercises
Reading Questions
How can two solutions with different volumes have the same concentration?
How can you figure out how many moles of solute you have in a solution with a specific concentration?
Reason and Apply
Draw molecular views for blue dye solutions that are 0.50 M, 0.25 M, and 0.10 M.
What portion of 1.0 L of 0.50 M blue dye solution has the same number of moles as 1.0 L of 0.25 M blue dye solution?
Glucose and sucrose are two different types of sugar. Consider these aqueous solutions:
 (left) 1.0 M C6H12O6 (glucose), (middle) 1.0 M C12H22O11 (sucrose), (right) 1.0 M C12H22O11 (sucrose)
(left) 1.0 M C6H12O6 (glucose), (middle) 1.0 M C12H22O11 (sucrose), (right) 1.0 M C12H22O11 (sucrose)Which solution has the most molecules? Explain.
Which solution has the greatest concentration? Explain.
Which solution has the most mass? Explain.
417
How many moles of sodium cations, Na+ are dissolved in a 1.0 L sample of each solution listed below?
0.10 M NaCl
3.0 M Na2SO4
0.30 M Na3PO4
Draw particle views for 1.0 M NaCl, 2.0 M NaCl, and 1.0 M Na2S. Use different symbols for each type of ion. Circle the solution(s) with the least total number of ions.
Determine the number of moles of solute in each of these aqueous solutions.
50 L of 0.10 M NaCl
0.25 L of 3.0 M C6H12O6
35 mL of 12.0 M HCl
300 mL of 0.025 M NaOH
How many liters of each solution do you need to get 3.0 mol HCl?
12.0 M HCl
2 M HCl
0.5 M HCl
0.010 M HCl