LESSON 4: Mass Communication: Mass and Volume
13
THINK ABOUT IT
ASTRONOMY CONNECTION
ASTRONOMY
CONNECTION
The words weight and mass are often used interchangeably. However, the difference between weight and mass is apparent when you consider astronauts on a spacewalk. The astronauts weigh much less than they do on Earth, but they have not gotten skinnier. Even in space, they have the same mass.

Suppose you have two samples of gold, a gold ring and a gold nugget. Is there more gold in the ring or in the nugget? They feel similar in weight, and they look fairly similar in volume. While your senses can give you valuable information, they can’t tell you exactly how much gold you have in each sample.
How do you determine the masses and volumes of different substances?
To answer this question, you will explore
Measuring Volume
Comparing Mass and Volume
Measuring Volume
EXPLORING THE TOPIC
Measuring Volume
As you learned in Lesson 3, volume is a measure of size, or how much space each sample takes up.
There are two common ways of measuring the volume of solids: (1) by measuring their dimensions and using a geometric formula and (2) by water displacement. The first method is convenient if the object has a regular shape. The second method is more convenient for irregularly shaped objects.
USING GEOMETRIC FORMULAS TO DETERMINE VOLUME
If a solid is rectangular, you can find its volume by measuring its three dimensions—length, width, and height—and multiplying these three values. Volume measured in this way is reported in cubic units such as cubic centimeters, cm3; cubic meters, m3; or cubic inches, in3. The formula for volume is
V = lwh
Consider these two solid blocks. You can use the formula to figure out their volumes.

V = lwh
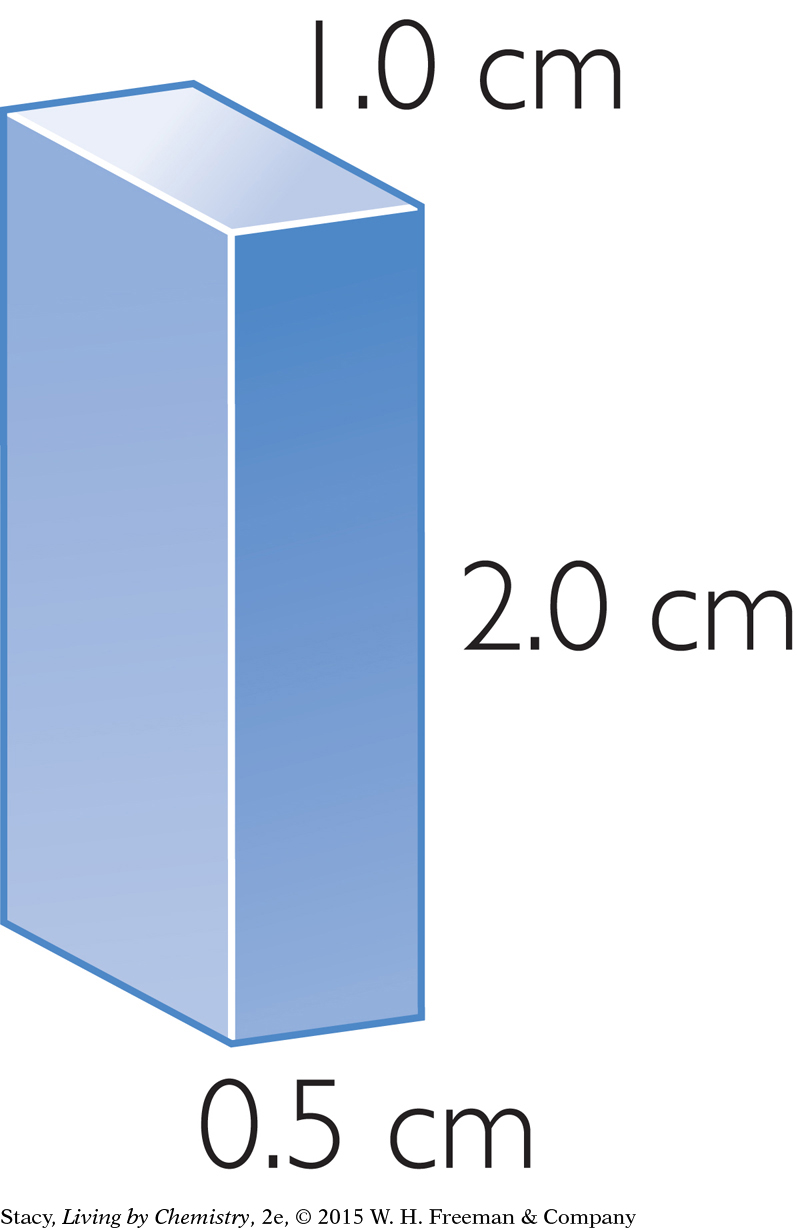
= 1.0 cm · 1.0 cm · 1.0 cm
= 1.0 cm3
V = lwh
= 1.0 cm · 0.5 cm · 2.0 cm
= 1.0 cm3
Notice that the two solids have different dimensions, but they have the same volume, 1.0 cubic centimeter.
USING WATER DISPLACEMENT TO DETERMINE VOLUME
14
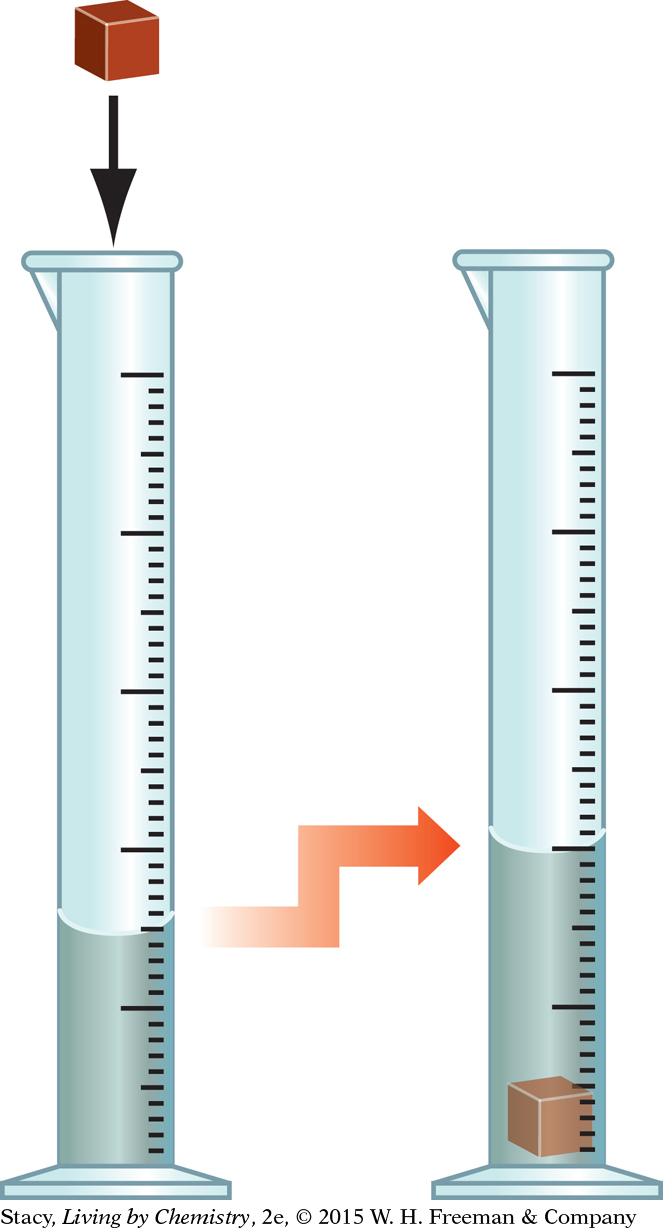
The second method of measuring the volume of a solid object is called water displacement. First, pour water into a graduated cylinder. Next, add the object whose volume you are measuring. An object takes up space, so it displaces some of the water when it is placed in the graduated cylinder. This causes the water level to rise by an amount equal to the volume of the object. If you read the volume of water in the graduated cylinder before you submerge the object and again after submerging it, the volume of the object is the difference between these two volumes.

Important to Know
One milliliter is exactly equal in volume to one cubic centimeter: 1 mL = 1 cm3.
Imagine you place a gold ring and a gold nugget in graduated cylinders partly filled with water. The graduated cylinder is marked in milliliters, mL. You observe that the water level rises by 2.0 mL in one container and by 4.0 mL in the other. The ring has a volume of 2.0 mL or 2.0 cm3 and the nugget 4.0 mL or 4.0 cm3.
Of course, the water displacement method works only for solids that do not dissolve in water! The solid object also needs to sink so that it is completely submerged. If the object floats, the volume reading will not be accurate.
Comparing Mass and Volume
Comparing Mass and Volume
CONSUMER CONNECTION
CONSUMER
CONNECTION
There are many different types of plastic. Soft-drink bottles are made of polyethylene terephthalate, also called PETE. Plastic pipes and outdoor furniture are made of polyvinyl chloride, also called PVC. Styrofoam cups are made of polystyrene.

Imagine that you have two objects with the same volume that are not made from the same material. You can compare their masses using a balance. The masses of 1.0 cm3 of gold and 1.0 cm3 of plastic are given in the table below along with the masses of the same volumes of wood, glass, and copper.

Important to Know
The rise in the water level does not depend on how heavy the cube is. The water-level rise depends only on the volume of the object.
Notice that 1.0 cm3 of gold is heavier than the same volume of any of the other materials. Thus, two objects can have exactly the same volume but different masses. The mass of the plastic depends on the type of plastic being considered. The mass of a 1.0 cm3 sample of plastic varies between 0.9 g and 1.5 g. Wood and glass also show variations. For instance, if you compare a 1.0 cm3 sample of solid wood from an oak tree with a 1.0 cm3 sample of solid wood from a pine tree, they will have different masses. The oak sample will be considerably heavier than the pine. A 1.0 cm3 sample of pure gold will always have a mass of 19.3 g because there is only one type of pure gold.
15
Example 1
Try to work out the answers yourself before reading the solutions.
Cubes of the Same Volume
Suppose you have two cubes. One cube is made of solid gold and the other cube is made of solid plastic. The sides of the cubes each measure 2.0 cm in length.
What is the volume of each cube?
How much water will each cube displace?
Solution
The volume of a cube is equal to length times width times height.
V = lwh
= 2.0 cm · 2.0 cm · 2.0 cm
= 8.0 cm3
Because 1 cm3 = 1 mL, you can reason that 8.0 cm3 = 8.0 mL. So each cube will displace the same amount of water, or 8.0 mL.
Example 2
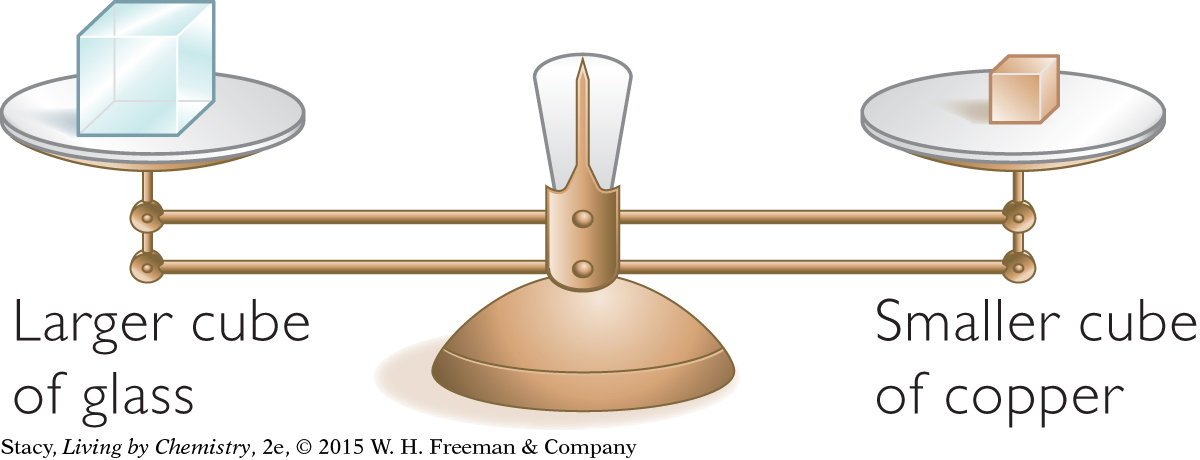
Cubes of the Same Mass
One cube is made of solid copper and another cube is made of solid glass. They have exactly the same mass. How do their volumes compare?
Solution
If you look at the table above, you will see that 1.0 cm3 of copper has much more mass than 1.0 cm3 of glass. Thus, for the two cubes to have the same mass, the copper cube must be much smaller than the glass cube.
LESSON SUMMARY
LESSON SUMMARY
16
How do you determine the masses and volumes of different substances?
KEY TERM
water displacement
The volume of a solid object is determined either by water displacement or by measuring its dimensions and using a geometric formula for volume. The mass of any solid sample is found by weighing it on a balance or scale. The relationship between mass and volume depends on the type of material being considered. Two objects may have the same volume but different masses, or two objects may have the same mass but different volumes.
Exercises
Reading Questions
Describe two ways to determine the volume of a solid object.
If you have two objects with equal volume, do they have the same mass? Explain your thinking.
Reason and Apply
Can you predict the volume of an object just by looking at it? Explain.
Can you predict the mass of an object just by looking at it? Explain.
If you stretch a rubber band, does it still have the same mass? Explain.

You submerge a piece of clay in water and measure the total volume. You change the shape of the clay and put it back into the same amount of water.
The total volume does not change. Explain why.
Does the total mass change? Explain.
Describe how you might find the volume of these items:
pancake mix
hair gel
a shoe box
a penny
lemonade
Draw two things with the same mass but different volumes.
Draw two things with the same volume but different masses.

Use the illustrations to answer these questions.
What is the volume of the liquid inside the container?
What is the volume of the rock in mL? In cm3?
Suppose that you have two cubes of exactly the same volume. You weigh them and find a mass of 8.91 g for one cube and 8.88 g for the other cube even though they are made of the same material. How is this possible?