LESSON 114: Now You See: Light Waves
581
THINK ABOUT IT
Light from the Sun travels a great distance through nearly empty space to reach Earth. It is hard to imagine how the light gets from one place to another. How does it travel and with what speed?
How is a wave model used to describe light?
To answer this question, you will explore
The Wave Model of Light
Wavelength, Frequency, and Speed
The Wave Model of Light
EXPLORING THE TOPIC
The Wave Model of Light
The ray model of light indicates the light path, but it does not reveal much about what light is and how it travels through space. The Greek philosopher Aristotle, born in 384 B.C.E., thought of light as wavelike in nature, traveling through space similar to the way ripples spread across a pond’s surface. Even though this view has undergone modification and elaboration through the centuries, it remains a useful model.
WAVES
Waves are created by a disturbance. For example, throw a pebble in a pond, and water waves spread out in circles of up-and-down motion. Or pluck a guitar string to make the entire string move back and forth.

Throw a pebble in a pond.
Nejron Photo/Shutterstock
|
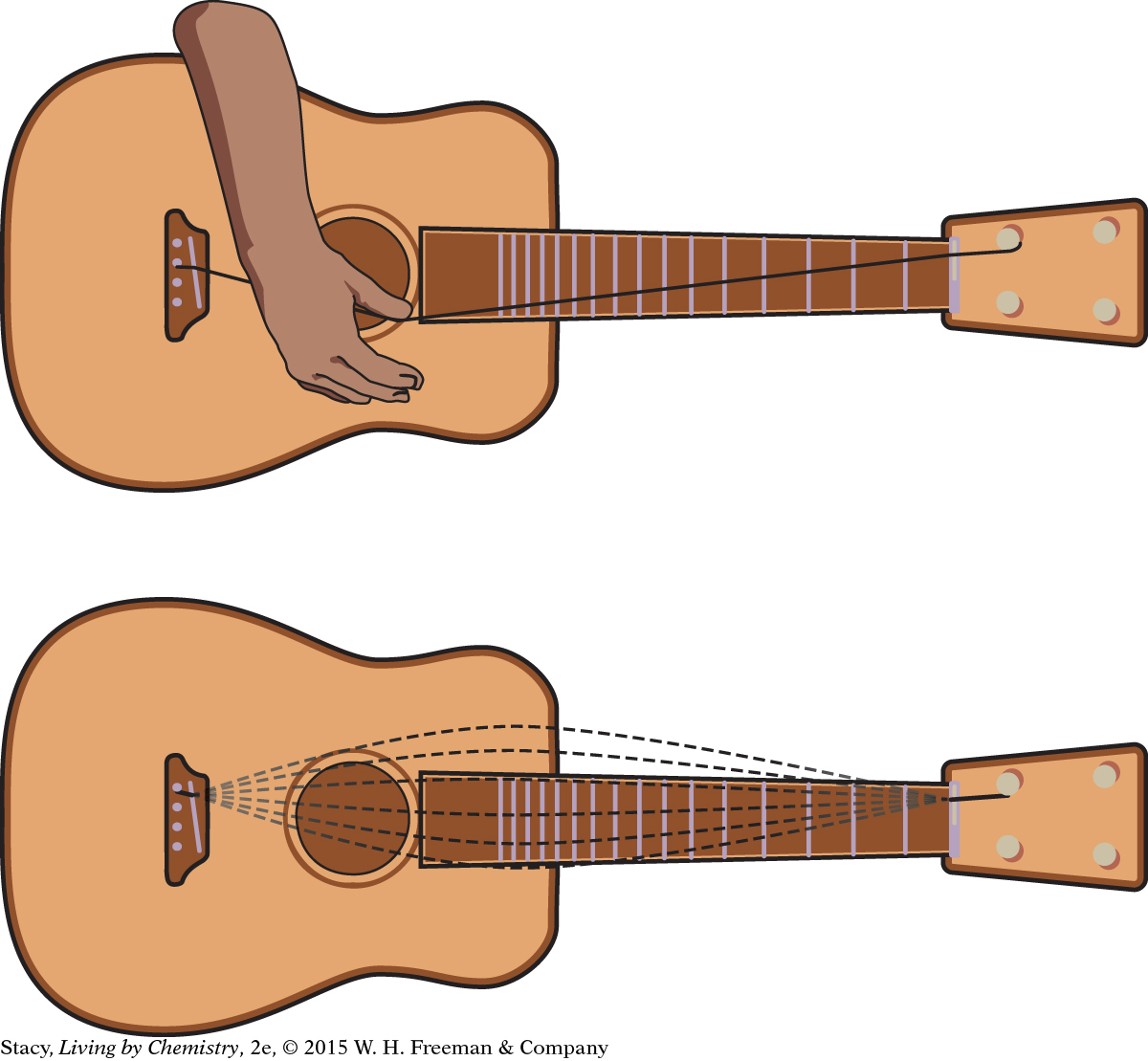
Pluck a guitar string.
|
You can also place a piece of rope on the floor and move one end back and forth while another person holds the other end fixed to create a single pulse of back-and-forth motion. This pulse travels along the rope. If you move one end back and forth in a continuous motion, the entire rope will move with a wave motion. Certain parts of the rope move left, while other parts move right.
582
Important to Know
Light waves differ from other waves in one important way: they can carry energy through empty space. All other waves can only travel through matter.
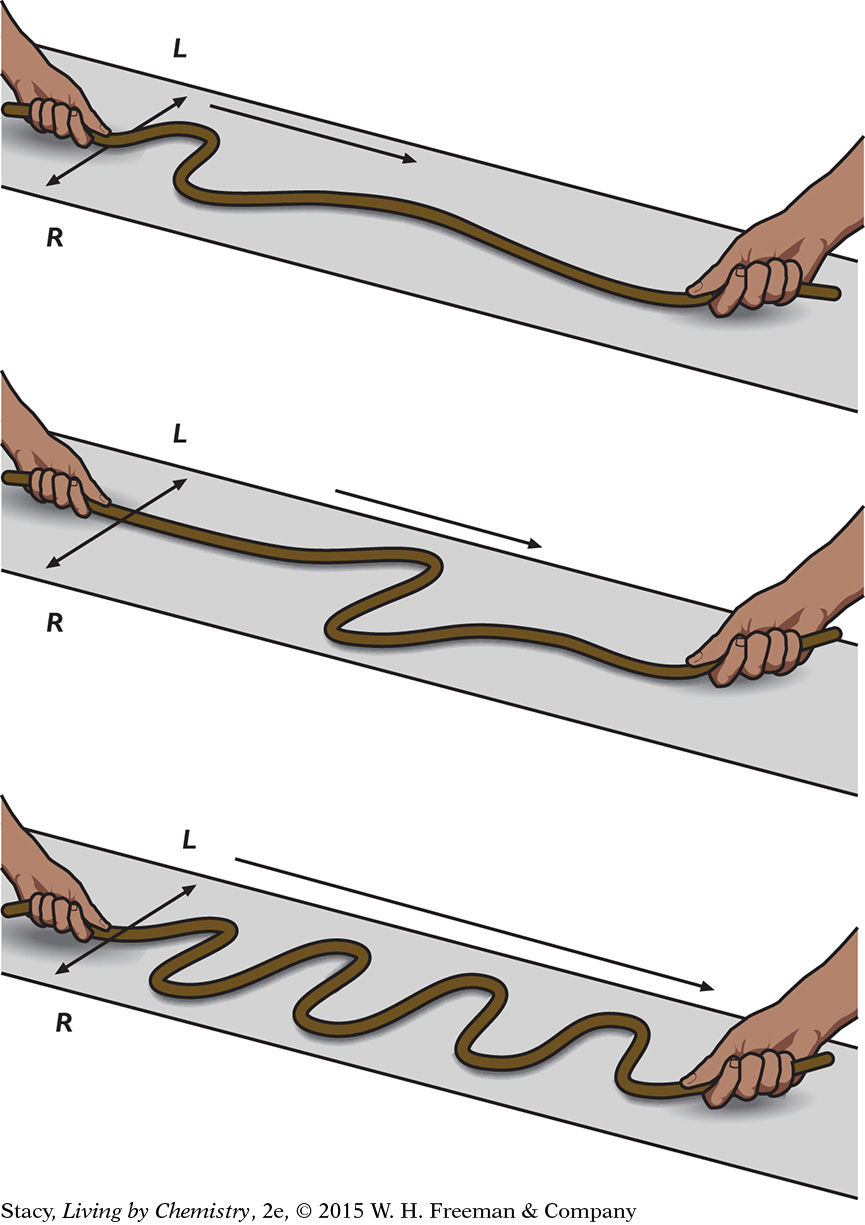
Notice that when a disturbance is created on one end of the rope, a person watching from the other end can detect the disturbance once the wave moves along the rope. Even from a large distance, it is possible to detect a disturbance as a wave reaches you and transfers its energy.
Light waves are thought to be ripples in space created by forces that oscillate up and down at a source, such as the Sun. The oscillations move as a wave over extremely long distances to Earth.
WAVE MEASUREMENTS
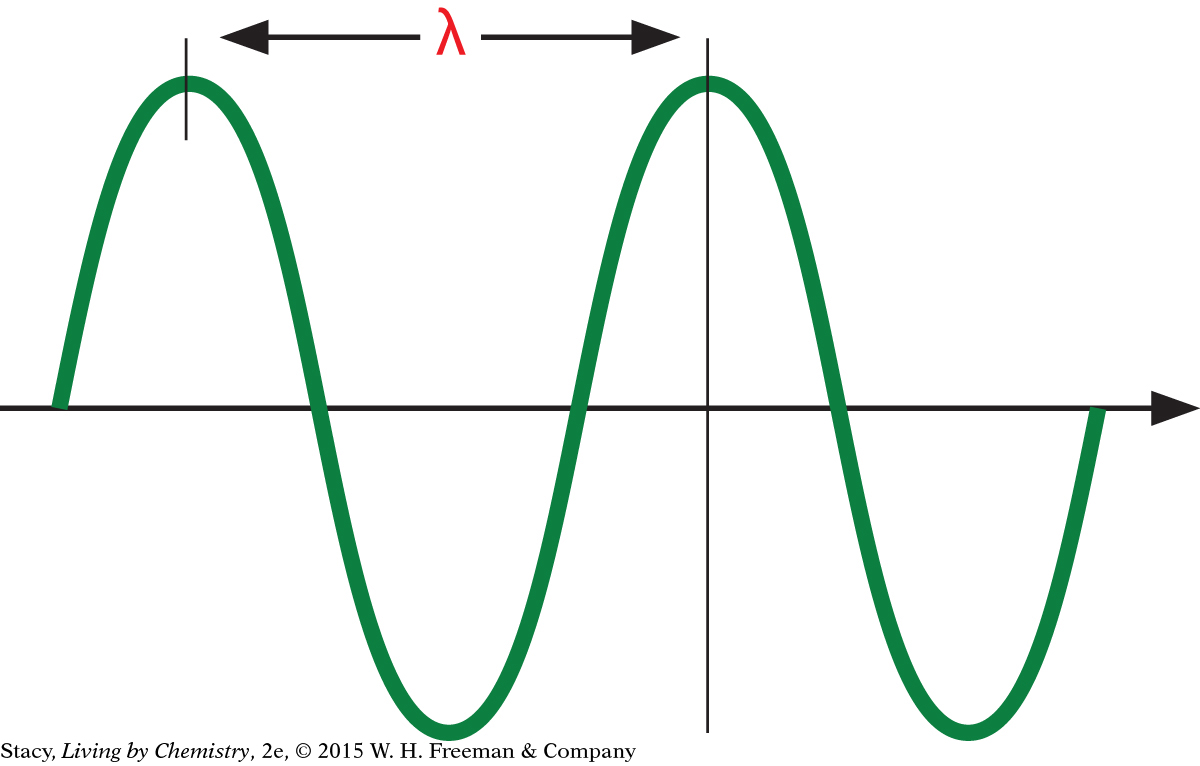
Two important measurements of waves are wavelength, λ, and frequency, f. The wavelength is the distance between two peaks or between two troughs of the wave measured in meters, m. The frequency is the measure of the number of waves that pass by a certain point in space per second, measured in hertz, Hz.
583
The wave below has different dimensions. Notice that the wavelength is shorter compared with the wave above. It also has more up-and-down motion. If you pick a place along the line and count waves that pass by, you will notice more waves per second for the wave with the shorter wavelength.
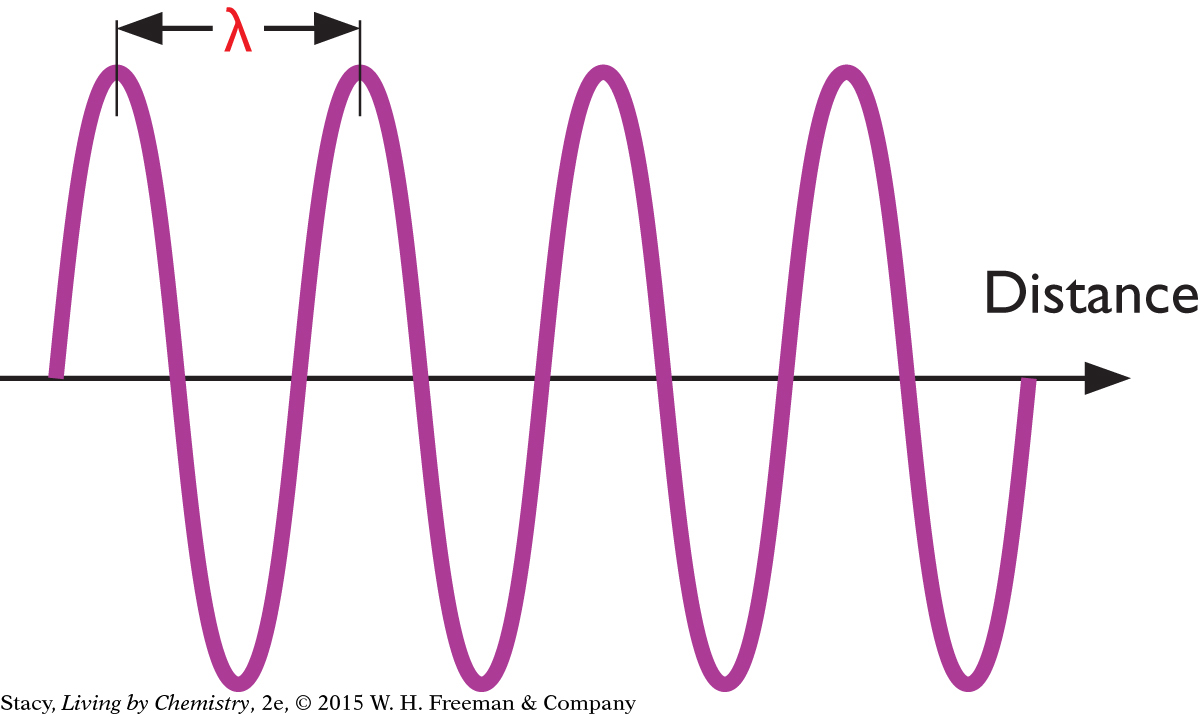
Notice that as the wavelength decreases, the frequency increases. And as the wavelength increases, the frequency decreases.
Wavelength, Frequency, and Speed
Wavelength, Frequency, and Speed
The bar provides the sequence of colors of the rainbow from red to violet. There are names for many of the colors, but not all of them. The six main categories are red, orange, yellow, green, blue, and violet. We tend to use labels such as red-orange and blue-green to refer to the colors in between the six main categories.

The wave model of light is useful in considering the differences and similarities of light of different colors. What are the dimensions of the light waves of various colors?
WAVES OF COLORED LIGHT
The light waves of different colors have characteristic wavelengths and frequencies. The table below gives the wavelength, frequency, and speed of light in a vacuum for the waves of five different colors. Take a moment to notice the trends.

584
PHYSICS CONNECTION
PHYSICS
CONNECTION
Unlike light, sound does not travel through empty space—only through gases, liquids, and solids. This is because sound causes wavelike motion of the atoms and molecules in these substances. The speed of sound waves is much slower than light waves, and vehicles, like this aircraft, can reach the speed of sound.

The wavelengths of visible light measured in meters, m, range from about 7.5 × 10–7 m for deep red light to 3.9 × 10–7 m for deep violet light. This dimension on the order of 10–7 m, or 0.0000001 m, is about the size of a large virus, one of the smallest things that can be seen using an optical microscope. Notice that the wavelength decreases from red to violet.
The frequencies, measured in inverse seconds, 1/s or s–1 or hertz, Hz, range from 4.0 × 1014 Hz for deep red light to 7.7 × 1014 Hz for deep violet light. This dimension on the order of 1014 Hz is huge. It is 100 trillion or 100,000,000,000,000 up-and-down motions, or oscillations, per second. Notice that the frequency increases from red to violet.
In empty space, all colors of light travel with the same speed, called the speed of light, c = 3 × 108 m/s. The distance of 108 m is 100 million meters, or 100,000,000 meters. If you could travel at the speed of light, you would be able to make seven-and-a-half trips around Earth’s equator in 1 second. This speed is extremely fast. It is not possible to cause visible objects to move at this speed!
Big Idea
Big Idea
All colors of light travel with the same speed in a vacuum, called the speed of light.
A relationship exists among the wavelength, frequency, and speed of light waves:
λ × f = c = 3 × 108 m/s
If you know the wavelength, you can calculate the frequency of colored light. And if you know the frequency, you can calculate the wavelength of colored light. The speed of light is the proportionality constant: frequency and wavelength are inversely proportional.

ANTHROPOLOGY CONNECTION
ANTHROPOLOGY
CONNECTION
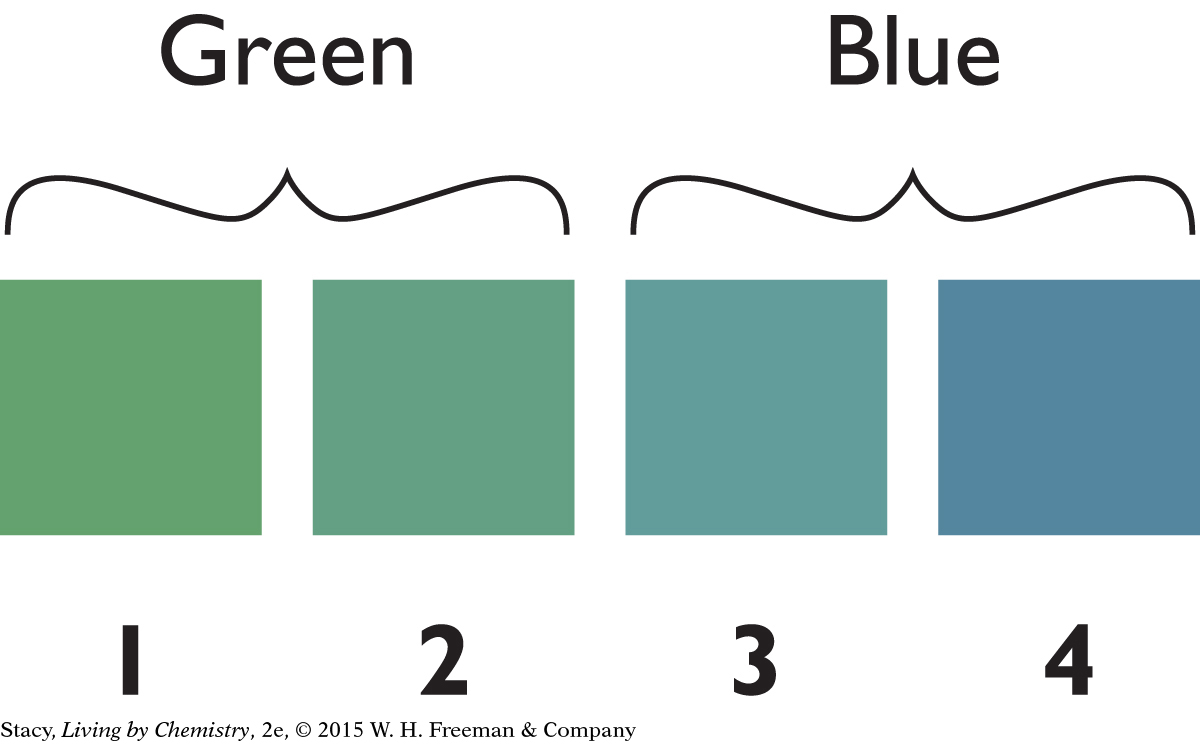
Does the language you speak influence your perception of color? Cognitive scientists have evidence that if you have a word for a specific color, you can pick that color out from among others. For example, some cultures do not distinguish between blue and green. What do you call these four colors, green or blue?
Example
Wavelength of Colored Light
Imagine a light wave with the frequency of 7.5 × 1014 Hz.
What is the wavelength of this light wave?
Use the table on page 583 to determine the approximate color of the light.
Solution
The wavelength and frequency of colored light are related by the equation:
λ × f = c
Rearrange the equation to solve for wavelength:

Substitute values for the frequency and speed of light:
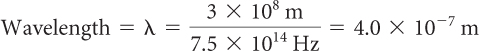
The wavelength and frequency indicate that the color is at the violet end of the rainbow.
585
LESSON SUMMARY
LESSON SUMMARY
How is a wave model used to describe light?
KEY TERMS
light wave
wavelength
frequency
speed of light
It is useful to characterize different colors of light with a wave model. This model treats light as a wave that travels through space. Light waves have a wavelength, λ (pronounced lambda), which is the distance between the peaks of the waves. The number of waves that pass by per second is called the frequency, f. Wavelength is typically reported in meters, m, and frequency is reported in hertz, Hz = 1/s. Different colors of light have different wavelengths and frequencies. However, all colors of light travel at the same speed, called the speed of light, c. A relationship exists among the wavelength, frequency, and speed of light waves: λ × f = c, where c = 3 × 108 m/s. Assigning a wavelength to different colors of light provides a precise continuous scale for all the different colors of the rainbow.
Exercises
Reading Questions
Explain how to determine the wavelength, λ, of a wave. What would you need to know?
Explain how to determine the frequency, f, of a wave. What would you need to know?
Reason and Apply
Draw sketches of two waves to show how green light and blue light differ from one another.
What are the approximate wavelengths of these two waves?
What are the approximate frequencies of these two waves?
How fast are these waves traveling?
Imagine a wave of light with the frequency of 4.1 × 1014 Hz.
What is the wavelength of this light wave?
Use the table on page 583 to determine the approximate color of the light.
Imagine a wave of light with the wavelength of 5.1 × 10–7 m.
What is the frequency of this light wave?
Use the table on page 583 to determine the approximate color of the light.
Why might it be useful to describe colors in terms of wavelength rather than simply using words?