PROBLEMS AND APPLICATIONS
To access online learning resources, visit  for Macroeconomics, 9e at www.macmillanhighered.com/launchpad/mankiw9e
for Macroeconomics, 9e at www.macmillanhighered.com/launchpad/mankiw9e
Question 15.5
1. Derive the long-run equilibrium for the dynamic AD–AS model. Assume there are no shocks to demand or supply (εt = υt = 0) and inflation has stabilized (πt = πt−1), and then use the five equations in Table 15-1 to derive the value of each variable in the model. Be sure to show each step you follow.
Question 15.6
2. Suppose the monetary-policy rule has the wrong natural rate of interest. That is, the central bank follows this rule:
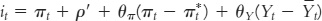
where ρ′ does not equal ρ, the natural rate of interest in the goods demand equation. The rest of the dynamic AD–AS model is the same as in the chapter. Solve for the long-run equilibrium under this policy rule. Explain in words the intuition behind your solution.
Question 15.7
3. “If a central bank wants to achieve lower nominal interest rates, it has to raise the nominal interest rate.” Explain in what way this statement makes sense.
Question 15.8
4. The sacrifice ratio is the accumulated loss in output that results when the central bank lowers its target for inflation by 1 percentage point. For the parameters used in the text simulation (see the FYI box), what is the implied sacrifice ratio? Explain.
Question 15.9
5. The text analyzes the case of a temporary shock to the demand for goods and services. Suppose, however, that εt were to increase permanently. What would happen to the economy over time? In particular, would the inflation rate return to its target in the long run? Why or why not? (Hint: It might be helpful to solve for the long-run equilibrium without the assumption that εt equals zero.) How might the central bank alter its policy rule to deal with this issue?
Question 15.10
6. Suppose a central bank does not satisfy the Taylor principle; in particular, assume that θπ is slightly less than zero, so the nominal interest rate rises less than one-for-one with inflation. Use a graph similar to Figure 15-13 to analyze the impact of a supply shock. Does this analysis contradict or reinforce the Taylor principle as a guideline for the design of monetary policy?
Question 15.11
7. The text assumes that the natural rate of interest ρ is a constant parameter. Suppose instead that it varies over time, so now it has to be written as ρt.
How would this change affect the equations for dynamic aggregate demand and dynamic aggregate supply?
How would a shock to ρt affect output, inflation, the nominal interest rate, and the real interest rate?
Can you see any practical difficulties that a central bank might face if ρt varied over time?
Question 15.12
8. Suppose that people’s expectations of inflation are subject to random shocks. That is, instead of being merely adaptive, expected inflation in period t, as seen in period t − 1, is Et−1πt = πt−1 + ηt−1, where ηt−1 is a random shock. This shock is normally zero, but it deviates from zero when some event beyond past inflation causes expected inflation to change. Similarly, Etπt+1 = πt + ηt.
Derive both the dynamic aggregate demand (DAD) equation and the dynamic aggregate supply (DAS) equation in this slightly more general model.
Suppose that the economy experiences an inflation scare. That is, in period t, for some reason people come to believe that inflation in period t + 1 is going to be higher, so ηt is greater than zero (for this period only). What happens to the DAD and DAS curves in period t? What happens to output, inflation, and nominal and real interest rates in that period? Explain.
What happens to the DAD and DAS curves in period t + 1? What happens to output, inflation, and nominal and real interest rates in that period? Explain.
What happens to the economy in subsequent periods?
In what sense are inflation scares self-fulfilling?
474
Question 15.13
9. Use the dynamic AD–AS model to solve for inflation as a function of only lagged inflation and supply and demand shocks. (Assume target inflation is constant.)
According to the equation you have derived, does inflation return to its target after a shock? Explain. (Hint: Look at the coefficient on lagged inflation.)
Suppose the central bank does not respond to changes in output but only to changes in inflation, so that θY = 0. How, if at all, would this fact change your answer to part (a)?
Suppose the central bank does not respond to changes in inflation but only to changes in output, so that θπ = 0. How, if at all, would this fact change your answer to part (a)?
Suppose the central bank does not follow the Taylor principle but instead raises the nominal interest rate only 0.8 percentage point for each percentage-point increase in inflation. In this case, what is θπ? How does a shock to demand or supply influence the path of inflation?
1 John B. Taylor, “Discretion Versus Policy Rules in Practice,” Carnegie-Rochester Conference Series on Public Policy 39 (1993): 195–214.
2 These estimates are derived from Table VI of Richard Clarida, Jordi Gali, and Mark Gertler, “Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory,” Quarterly Journal of Economics 115, no. 1 (February 2000): 147–180.
3 For a brief introduction to this topic, see Argia Sbordone, Andrea Tambalotti, Krishna Rao, and Kieran Walsh, “Policy Analysis Using DSGE Models: An Introduction,” Federal Reserve Bank of New York Economic Policy Review 16, no. 2 (2010): 23–43. An important early paper in the development of DSGE models is Julio Rotemberg and Michael Woodford, “An Optimization-Based Econometric Framework for the Evaluation of Monetary Policy,” NBER Macroeconomics Annual 12 (1997): 297–346. A good textbook introduction to this literature is Jordi Galí, Monetary Policy, Inflation, and the Business Cycle (Princeton, NJ: Princeton University Press, 2008).