8.1 The Accumulation of Capital
The Solow growth model is designed to show how growth in the capital stock, growth in the labor force, and advances in technology interact in an economy as well as how they affect a nation’s total output of goods and services. We will build this model in a series of steps. Our first step is to examine how the supply and demand for goods determine the accumulation of capital. In this first step, we assume that the labor force and technology are fixed. We then relax these assumptions by introducing changes in the labor force later in this chapter and by introducing changes in technology in the next.
The Supply and Demand for Goods
The supply and demand for goods played a central role in our static model of the closed economy in Chapter 3. The same is true for the Solow model. By considering the supply and demand for goods, we can see what determines how much output is produced at any given time and how this output is allocated among alternative uses.
213
The Supply of Goods and the Production Function The supply of goods in the Solow model is based on the production function, which states that output depends on the capital stock and the labor force:
Y = F(K, L).
The Solow growth model assumes that the production function has constant returns to scale. This assumption is often considered realistic, and, as we will see shortly, it helps simplify the analysis. Recall that a production function has constant returns to scale if
zY = F(zK, zL)
for any positive number z. That is, if both capital and labor are multiplied by z, the amount of output is also multiplied by z.
Production functions with constant returns to scale allow us to analyze all quantities in the economy relative to the size of the labor force. To see that this is true, set z = 1/L in the preceding equation to obtain
Y/L = F(K/L, 1).
This equation shows that the amount of output per worker Y/L is a function of the amount of capital per worker K/L. (The number 1 is constant and thus can be ignored.) The assumption of constant returns to scale implies that the size of the economy—
Because the size of the economy does not matter, it will prove convenient to denote all quantities in per-
y = f(k),
where we define f(k) = F(k, 1). Figure 8-1 illustrates this production function.
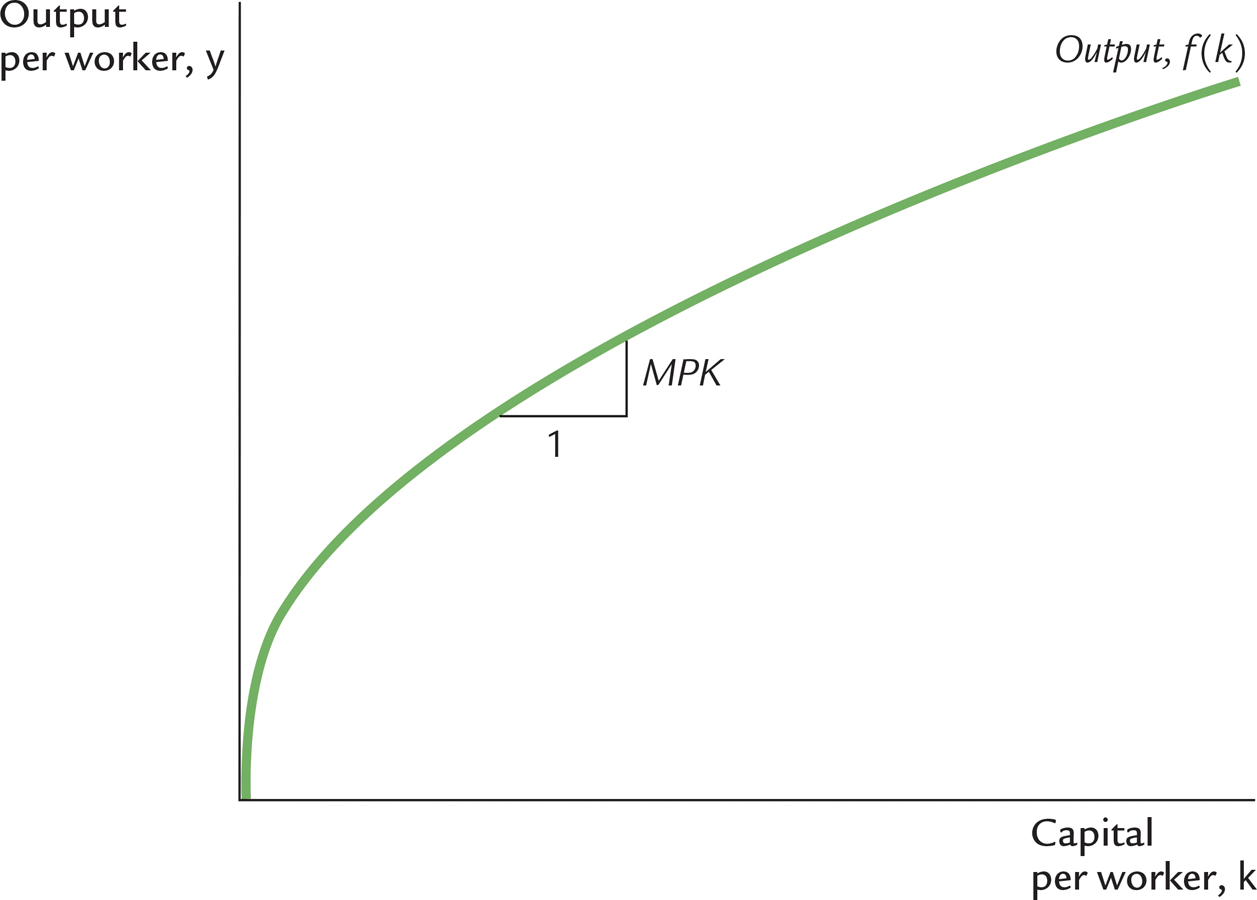
The slope of this production function shows how much extra output a worker produces when given an extra unit of capital. This amount is the marginal product of capital MPK. Mathematically, we write
MPK = f(k + 1) − f(k).
Note that in Figure 8-1, as the amount of capital increases, the production function becomes flatter, indicating that the production function exhibits diminishing marginal product of capital. When k is low, the average worker has only a little capital to work with, so an extra unit of capital is very useful and produces a lot of additional output. When k is high, the average worker has a lot of capital already, so an extra unit increases production only slightly.
The Demand for Goods and the Consumption Function The demand for goods in the Solow model comes from consumption and investment. In other words, output per worker y is divided between consumption per worker c and investment per worker i:
y = c + i.
214
This equation is the per-
The Solow model assumes that each year people save a fraction s of their income and consume a fraction (1 − s). We can express this idea with the following consumption function:
c = (1 − s)y,
where s, the saving rate, is a number between zero and one. Keep in mind that various government policies can potentially influence a nation’s saving rate, so one of our goals is to find what saving rate is desirable. For now, however, we just take the saving rate s as given.
To see what this consumption function implies for investment, substitute (1 − s)y for c in the national income accounts identity:
y = (1 − s)y + i.
Rearrange the terms to obtain
i = sy.
This equation shows that investment equals saving, as we first saw in Chapter 3. Thus, the rate of saving s is also the fraction of output devoted to investment.
We have now introduced the two main ingredients of the Solow model—
215
Growth in the Capital Stock and the Steady State
At any moment, the capital stock is a key determinant of the economy’s output, but the capital stock can change over time, and those changes can lead to economic growth. In particular, two forces influence the capital stock: investment and depreciation. Investment is expenditure on new plant and equipment, and it causes the capital stock to rise. Depreciation is the wearing out of old capital due to aging and use, and it causes the capital stock to fall. Let’s consider each of these forces in turn.
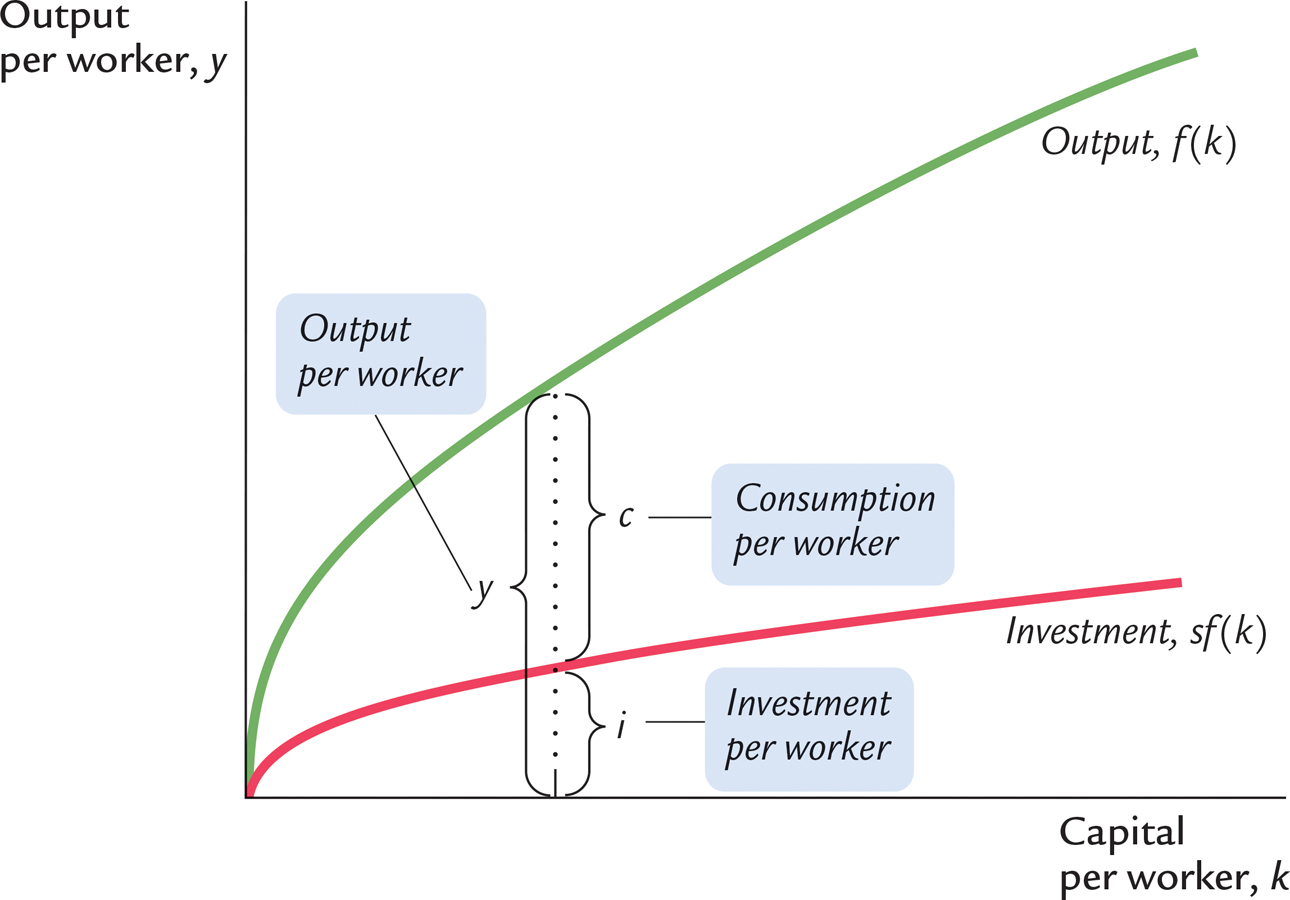
As we have already noted, investment per worker i equals sy. By substituting the production function for y, we can express investment per worker as a function of the capital stock per worker:
i = sf(k).
This equation relates the existing stock of capital k to the accumulation of new capital i. Figure 8-2 shows this relationship. This figure illustrates how, for any value of k, the amount of output is determined by the production function f(k), and the allocation of that output between consumption and investment is determined by the saving rate s.
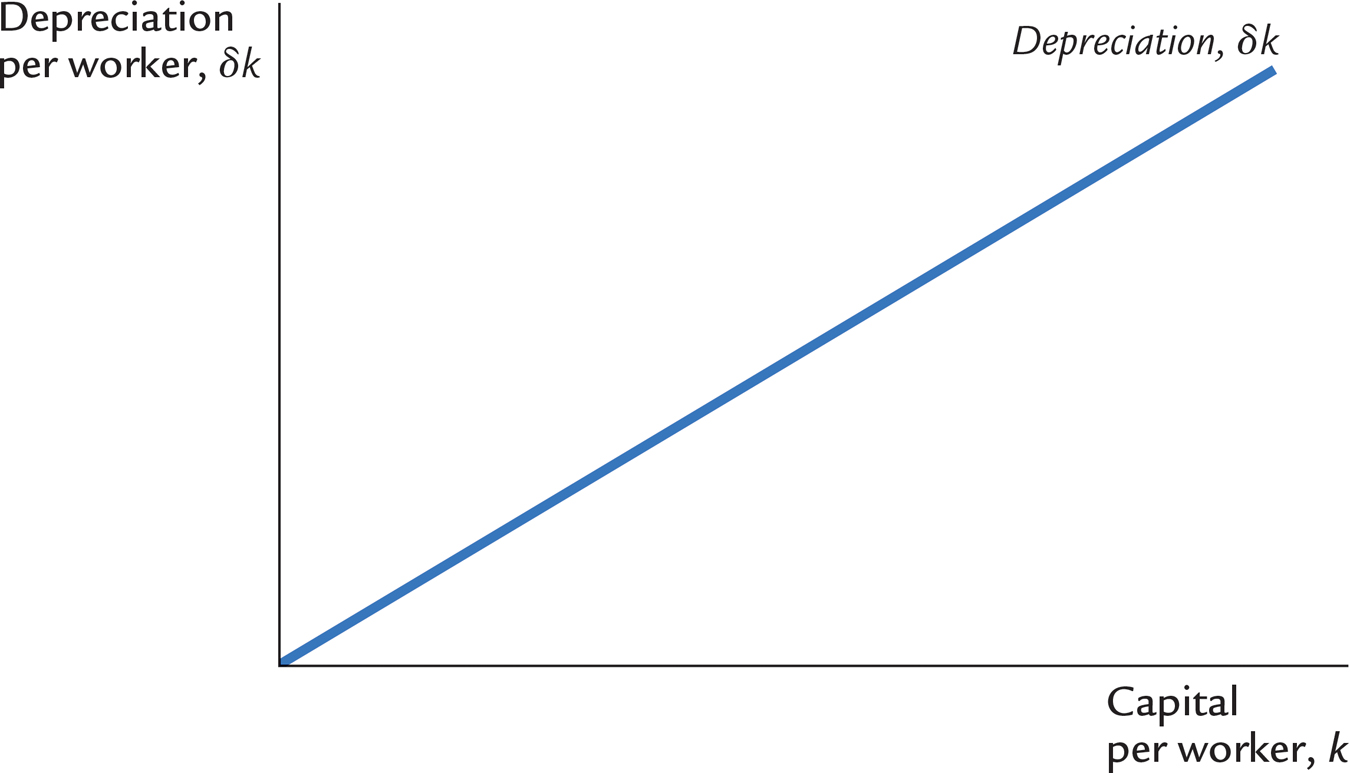
To incorporate depreciation into the model, we assume that a certain fraction δ of the capital stock wears out each year. Here δ (the lowercase Greek letter delta) is called the depreciation rate. For example, if capital lasts an average of 25 years, then the depreciation rate is 4 percent per year (δ = 0.04). The amount of capital that depreciates each year is δk. Figure 8-3 shows how the amount of depreciation depends on the capital stock.
216
We can express the impact of investment and depreciation on the capital stock with this equation:
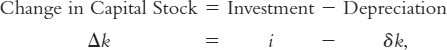
where Δk is the change in the capital stock between one year and the next. Because investment i equals sf(k), we can write this as
Δk = sf(k) − δk.
Figure 8-4 graphs the terms of this equation—
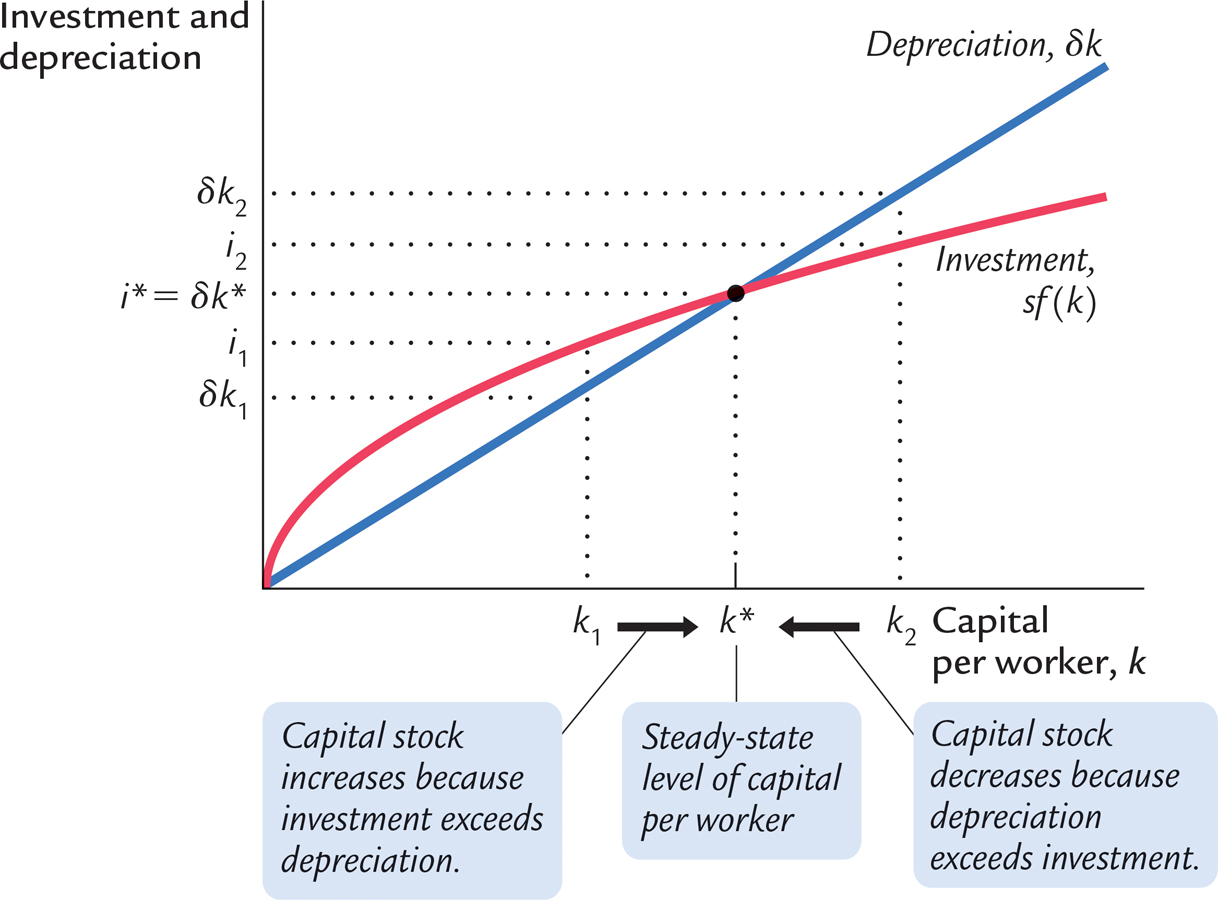
As Figure 8-4 shows, there is a single capital stock k* at which the amount of investment equals the amount of depreciation. If the economy finds itself at this level of the capital stock, the capital stock will not change because the two forces acting on it—
The steady state is significant for two reasons. As we have just seen, an economy at the steady state will stay there. In addition, and just as important, an economy not at the steady state will go there. That is, regardless of the level of capital with which the economy begins, it ends up with the steady-
To see why an economy always ends up at the steady state, suppose that the economy starts with less than the steady-
217
Similarly, suppose that the economy starts with more than the steady-
Approaching the Steady State: A Numerical Example
Let’s use a numerical example to see how the Solow model works and how the economy approaches the steady state. For this example, we assume that the production function is
Y = K1/2L1/2.
From Chapter 3, you will recognize this as the Cobb–
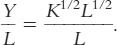
Rearrange to obtain
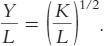
218
Because y = Y/L and k = K/L, this equation becomes
y = k1/2,
which can also be written as
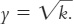
This form of the production function states that output per worker equals the square root of the amount of capital per worker.
To complete the example, let’s assume that 30 percent of output is saved (s = 0.3), that 10 percent of the capital stock depreciates every year (δ = 0.1), and that the economy starts off with 4 units of capital per worker (k = 4). Given these numbers, we can now examine what happens to this economy over time.
We begin by looking at the production and allocation of output in the first year, when the economy has 4 units of capital per worker. Here are the steps we follow.
According to the production function
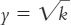 , the 4 units of capital per worker (k) produce 2 units of output per worker (y).
, the 4 units of capital per worker (k) produce 2 units of output per worker (y).Because 30 percent of output is saved and invested and 70 percent is consumed, i = 0.6 and c = 1.4.
Because 10 percent of the capital stock depreciates, δk = 0.4.
With investment of 0.6 and depreciation of 0.4, the change in the capital stock is Δk = 0.2.
Thus, the economy begins its second year with 4.2 units of capital per worker.
We can do the same calculations for each subsequent year. Table 8-2 shows how the economy progresses. Every year, because investment exceeds depreciation, new capital is added and output grows. Over many years, the economy approaches a steady state with 9 units of capital per worker. In this steady state, investment of 0.9 exactly offsets depreciation of 0.9, so the capital stock and output are no longer growing.
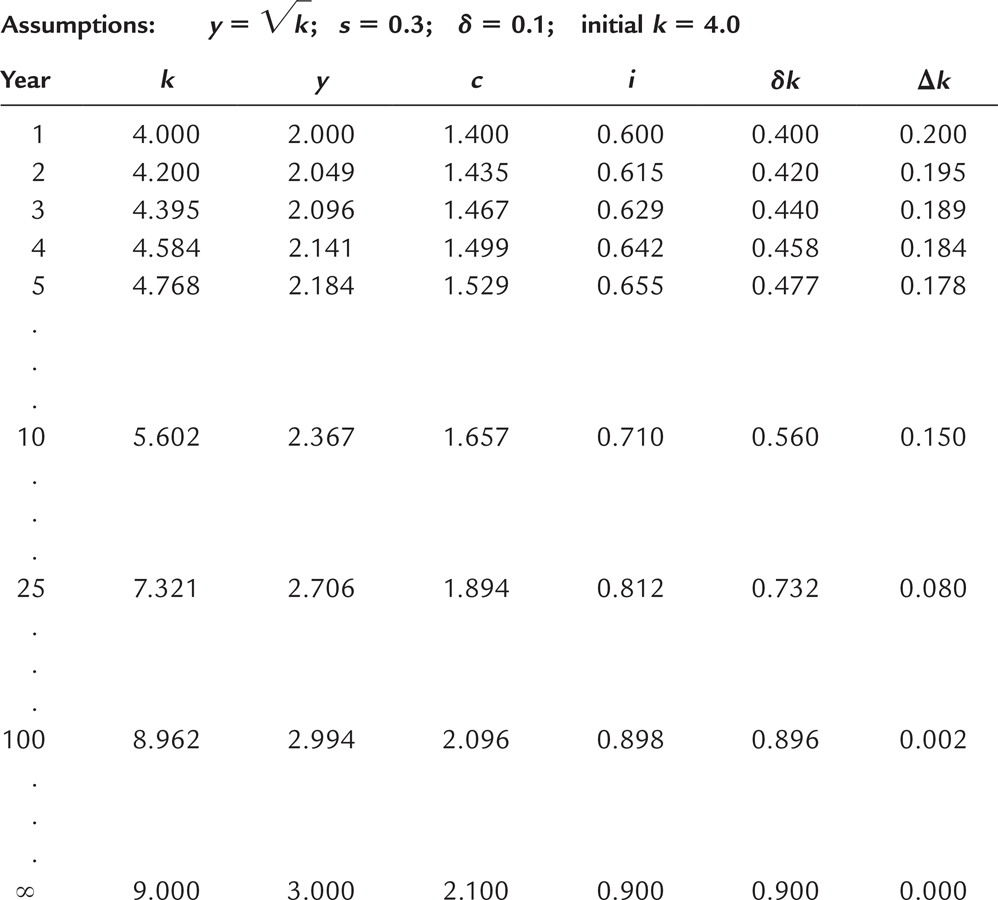
Following the progress of the economy for many years is one way to find the steady-
Δk = sf(k) − δk.
This equation shows how k evolves over time. Because the steady state is (by definition) the value of k at which Δk = 0, we know that
0 = sf(k*) − δk*,
or, equivalently,
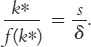
This equation provides a way of finding the steady-
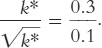
219
Now square both sides of this equation to find
k* = 9.
The steady-
CASE STUDY
The Miracle of Japanese and German Growth
Japan and Germany are two success stories of economic growth. Although today they are economic superpowers, in 1946 the economies of both countries were in shambles. World War II had destroyed much of their capital stocks. In both nations, output per person in 1946 was about half of what it had been before the war. In the following decades, however, these two countries experienced some of the most rapid growth rates on record. Between 1946 and 1972, output per person grew at 8.0 percent per year in Japan and 6.5 percent per year in Germany, compared to only 2.1 percent per year in the United States. Several other European economies damaged by the war also enjoyed rapid growth during this postwar period: for example, output per worker grew at 4.6 percent per year in France and 5.5 percent per year in Italy. But Japan and Germany are the two nations that experienced both the greatest devastation during the war and the most rapid growth after it.
220
Are these postwar experiences so surprising from the standpoint of the Solow growth model? Consider an economy in steady state. Now suppose that a war destroys some of the capital stock. (That is, suppose the capital stock drops from k* to k1 in Figure 8-4.) Not surprisingly, the level of output falls immediately. But if the saving rate—
Subsequent to their postwar growth miracles, both Japan and Germany settled down to moderate rates of growth, more similar to that of the United States. From 1972 to 2000, output per person grew at 2.4 percent per year in Japan and 1.8 percent per year in Germany, compared to 2.1 percent per year in the United States. This phenomenon is also what the Solow model predicts. As an economy gets closer to its steady state, it no longer experiences the higher-
Lest one take the wrong lesson from this historical episode, note that wartime destruction should not be seen as desirable. The fast growth in Japan and Germany during the postwar period merely caught them up to where they otherwise would have been. Moreover, unlike Japan and Germany, many war-
How Saving Affects Growth
The explanation of Japanese and German growth after World War II is not quite as simple as suggested in the preceding Case Study. Another relevant fact is that both Japan and Germany save and invest a higher fraction of their output than does the United States. To understand more fully the international differences in economic performance, we must consider the effects of different saving rates.
Consider what happens to an economy when its saving rate increases. Figure 8-5 shows such a change. The economy is assumed to begin in a steady state with saving rate s1 and capital stock k1*. When the saving rate increases from s1 to s2, the sf(k) curve shifts upward. At the initial saving rate s1 and the initial capital stock k1*, the amount of investment just offsets the amount of depreciation. Immediately after the saving rate rises, investment is higher, but the capital stock and depreciation are unchanged. Therefore, investment exceeds depreciation. The capital stock gradually rises until the economy reaches the new steady state k2*, which has a higher capital stock and a higher level of output than the old steady state.
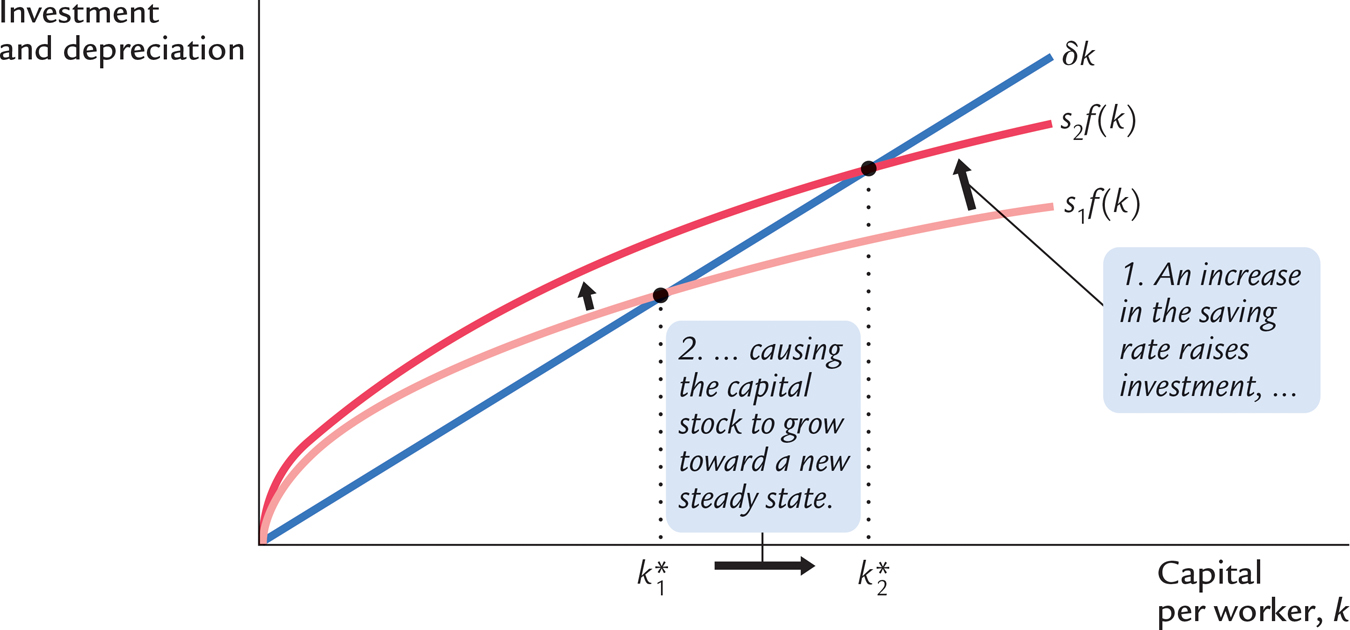
221
The Solow model shows that the saving rate is a key determinant of the steady-
What does the Solow model say about the relationship between saving and economic growth? Higher saving leads to faster growth in the Solow model, but only temporarily. An increase in the rate of saving raises growth only until the economy reaches the new steady state. If the economy maintains a high saving rate, it will maintain a large capital stock and a high level of output, but it will not maintain a high rate of growth forever. Policies that alter the steady-
Now that we understand how saving and growth interact, we can more fully explain the impressive economic performance of Germany and Japan after World War II. Not only were their initial capital stocks low because of the war, but their steady-
222
CASE STUDY
Saving and Investment Around the World
We started this chapter with an important question: Why are some countries so rich while others are mired in poverty? Our analysis has taken us a step closer to the answer. According to the Solow model, if a nation devotes a large fraction of its income to saving and investment, it will have a high steady-
Let’s now look at some data to see if this theoretical result in fact helps explain the large international variation in standards of living. Figure 8-6 is a scatterplot of data from about 100 countries. (The figure includes most of the world’s economies. It excludes major oil-
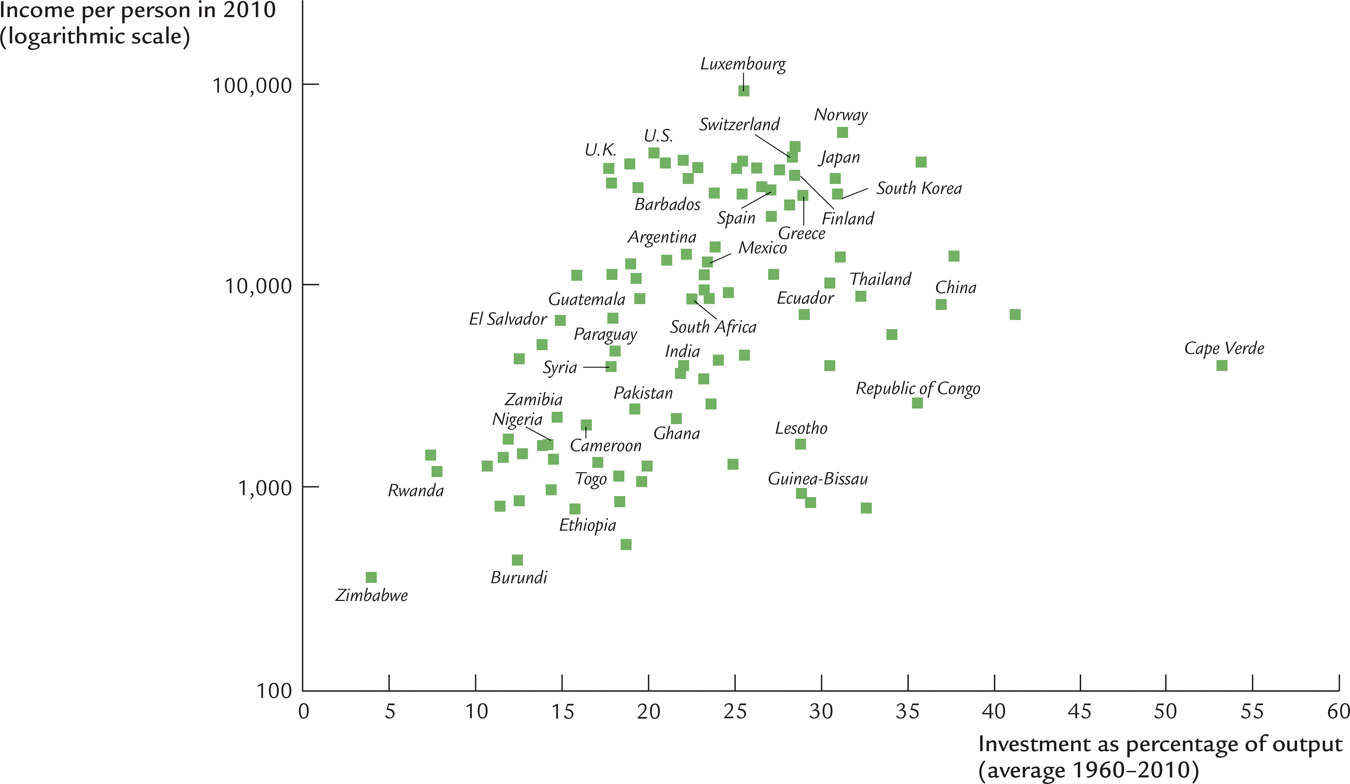
The positive correlation shown in this figure is an important fact, but it raises as many questions as it resolves. One might naturally ask, why do rates of saving and investment vary so much from country to country? There are many potential answers, such as tax policy, retirement patterns, the development of financial markets, and cultural differences. In addition, political stability may play a role: not surprisingly, rates of saving and investment tend to be low in countries with frequent wars, revolutions, and coups. Saving and investment also tend to be low in countries with poor political institutions, as measured by estimates of official corruption. A final interpretation of the evidence in Figure 8-6 is reverse causation: perhaps high levels of income somehow foster high rates of saving and investment. Unfortunately, there is no consensus among economists about which of the many possible explanations is most important.
The association between investment rates and income per person is an important clue as to why some countries are rich and others poor, but it is not the whole story. The correlation between these two variables is far from perfect. There must be other determinants of living standards beyond saving and investment. Later in this chapter and in the next one, we return to the international differences in income per person to see what other variables enter the picture. 
223