8.3 Population Growth
The basic Solow model shows that capital accumulation, by itself, cannot explain sustained economic growth: high rates of saving lead to high growth temporarily, but the economy eventually approaches a steady state in which capital and output are constant. To explain the sustained economic growth that we observe in most parts of the world, we must expand the Solow model to incorporate the other two sources of economic growth—
Instead of assuming that the population is fixed, as we did in Section 8-1 and Section 8-2, we now suppose that the population and the labor force grow at a constant rate n. For example, the U.S. population grows about 1 percent per year, so n = 0.01. This means that if 150 million people are working one year, then 151.5 million (1.01 × 150) are working the next year, and 153.015 million (1.01 × 151.5) the year after that, and so on.
The Steady State With Population Growth
How does population growth affect the steady state? To answer this question, we must discuss how population growth, along with investment and depreciation, influences the accumulation of capital per worker. As we noted before, investment raises the capital stock, and depreciation reduces it. But now there is a third force acting to change the amount of capital per worker: the growth in the number of workers causes capital per worker to fall.
We continue to let lowercase letters stand for quantities per worker. Thus, k = K/L is capital per worker, and y = Y/L is output per worker. Keep in mind, however, that the number of workers is growing over time.
The change in the capital stock per worker is
Δk = i − (δ + n)k.
This equation shows how investment, depreciation, and population growth influence the per-
We can think of the term (δ + n)k as defining break-
232
Our analysis with population growth now proceeds much as it did previously. First, we substitute sf(k) for i. The equation can then be written as
Δk = sf(k) − (δ + n)k.
To see what determines the steady-
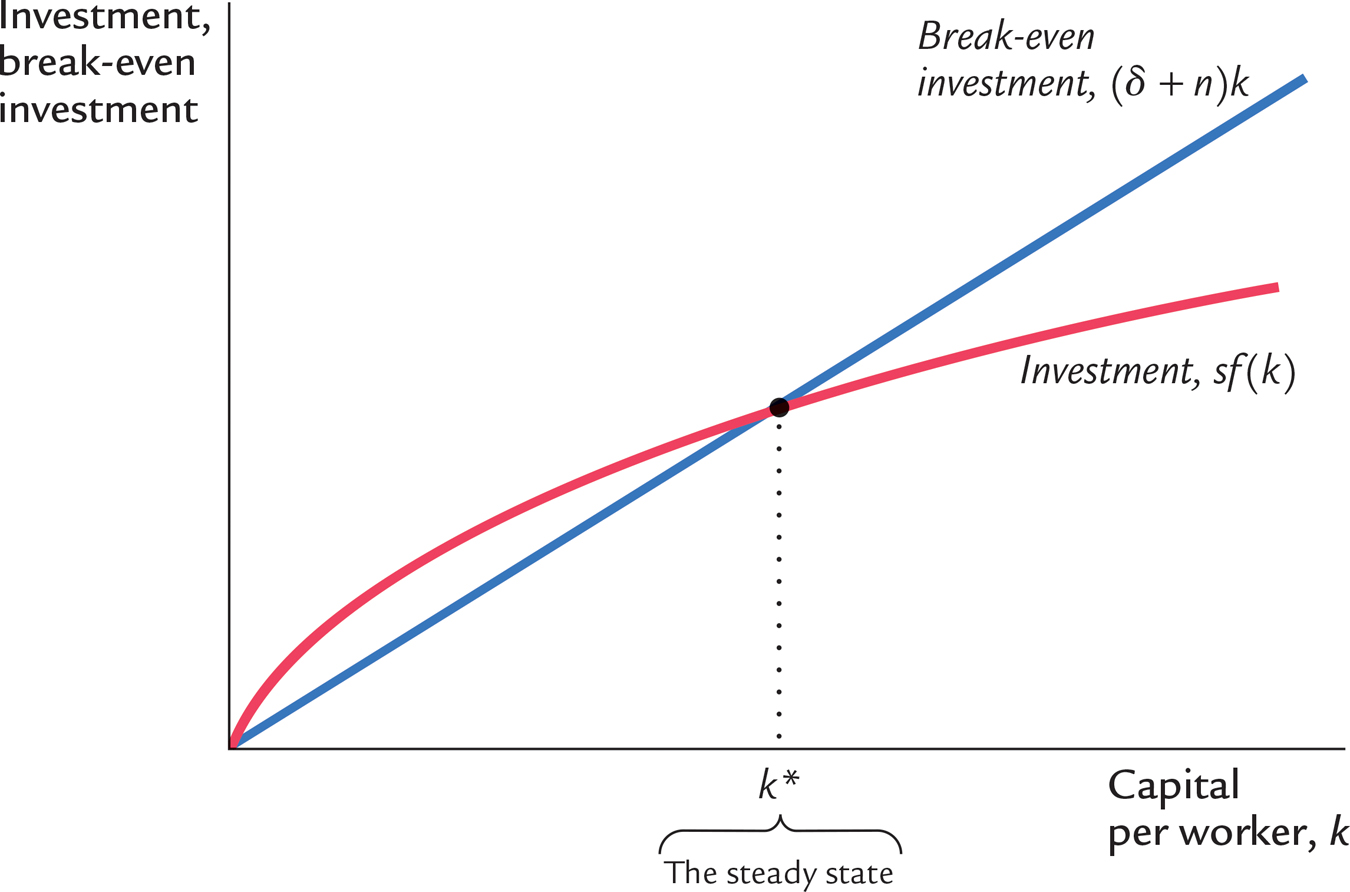
In the steady state, the positive effect of investment on the capital stock per worker exactly balances the negative effects of depreciation and population growth. That is, at k*, Δk = 0 and i* = δk* + nk*. Once the economy is in the steady state, investment has two purposes. Some of it (δk*) replaces the depreciated capital, and the rest (nk*) provides the new workers with the steady-
233
The Effects of Population Growth
Population growth alters the basic Solow model in three ways. First, it brings us closer to explaining sustained economic growth. In the steady state with population growth, capital per worker and output per worker are constant. Because the number of workers is growing at rate n, however, total capital and total output must also be growing at rate n. Hence, although population growth cannot explain sustained growth in the standard of living (because output per worker is constant in the steady state), it can help explain sustained growth in total output.
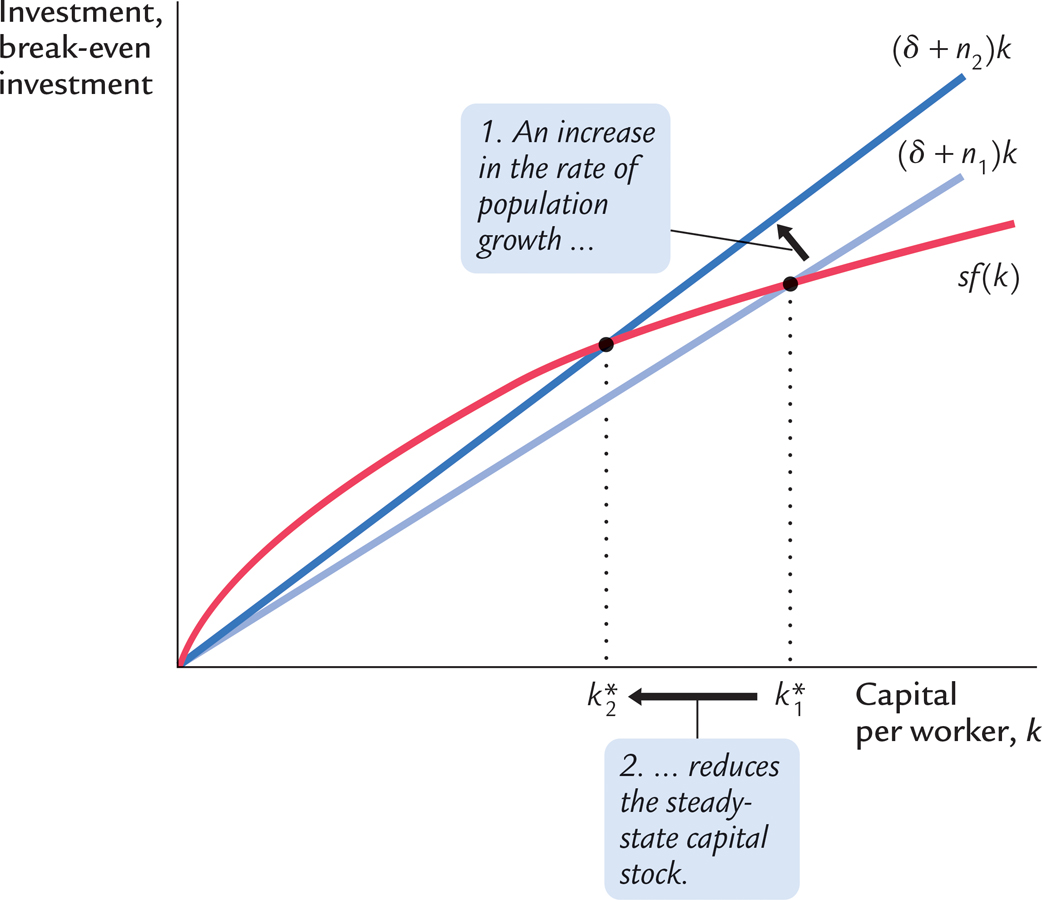
Second, population growth gives us another explanation for why some countries are rich and others are poor. Consider the effects of an increase in population growth. Figure 8-12 shows that an increase in the rate of population growth from n1 to n2 reduces the steady-
Finally, population growth affects our criterion for determining the Golden Rule (consumption-
c = y − i.
234
Because steady-
c* = f(k*) − (δ + n)k*.
Using an argument largely the same as before, we conclude that the level of k* that maximizes consumption is the one at which
MPK = δ + n,
or equivalently,
MPK − δ = n.
In the Golden Rule steady state, the marginal product of capital net of depreciation equals the rate of population growth.
CASE STUDY
Population Growth Around the World
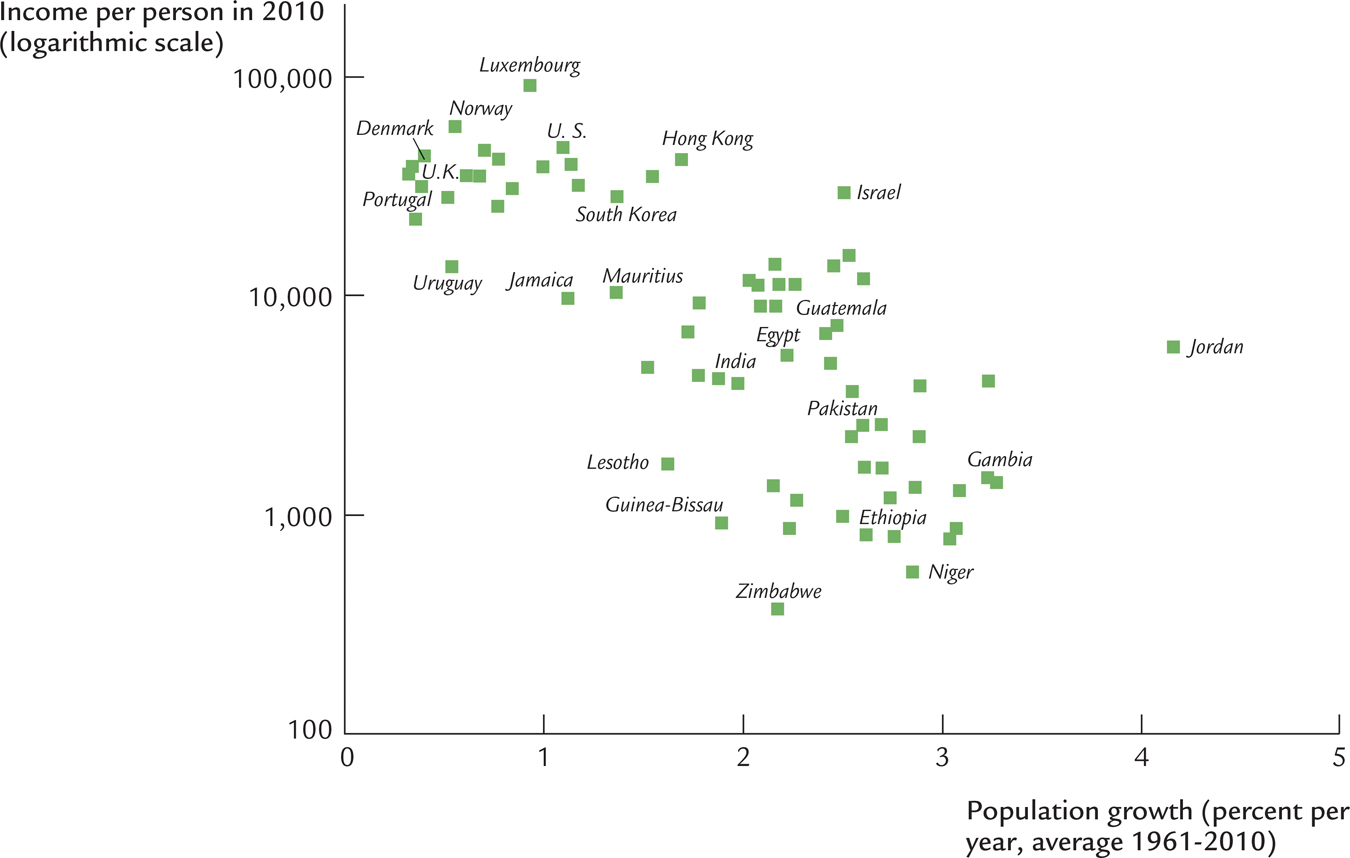
Let’s return now to the question of why standards of living vary so much around the world. The analysis we have just completed suggests that population growth may be one of the answers. According to the Solow model, a nation with a high rate of population growth will have a low steady-
Figure 8-13 is a scatterplot of data for the same countries examined in the previous Case Study (and in Figure 8-6). The figure shows that countries with high rates of population growth tend to have low levels of income per person. The international evidence is consistent with our model’s prediction that the rate of population growth is one determinant of a country’s standard of living.
This conclusion is not lost on policymakers. Those trying to pull the world’s poorest nations out of poverty, such as the advisers sent to developing nations by the World Bank, often advocate reducing fertility by increasing education about birth-
In interpreting the cross-
235
Alternative Perspectives on Population Growth
The Solow growth model highlights the interaction between population growth and capital accumulation. In this model, high population growth reduces output per worker because rapid growth in the number of workers forces the capital stock to be spread more thinly, so in the steady state, each worker is equipped with less capital. The model omits some other potential effects of population growth. Here we consider two—
236
The Malthusian Model In his book An Essay on the Principle of Population as It Affects the Future Improvement of Society, the early economist Thomas Robert Malthus (1766–
Malthus began by noting that “food is necessary to the existence of man” and that “the passion between the sexes is necessary and will remain nearly in its present state.” He concluded that “the power of population is infinitely greater than the power in the earth to produce subsistence for man.” According to Malthus, the only check on population growth was “misery and vice.” Attempts by charities or governments to alleviate poverty were counterproductive, he argued, because they merely allowed the poor to have more children, placing even greater strains on society’s productive capabilities.
The Malthusian model may have described the world when Malthus lived, but its prediction that mankind would remain in poverty forever has proven very wrong. The world population has increased about sevenfold over the past two centuries, but average living standards are much higher. Because of economic growth, chronic hunger and malnutrition are less common now than they were in Malthus’s day. Famines occur from time to time, but they are more often the result of unequal income distribution or political instability than the inadequate production of food.
Malthus failed to foresee that growth in mankind’s ingenuity would more than offset the effects of a larger population. Pesticides, fertilizers, mechanized farm equipment, new crop varieties, and other technological advances that Malthus never imagined have allowed each farmer to feed ever-
In addition, although the “passion between the sexes” is just as strong now as it was in Malthus’s day, the link between passion and population growth that Malthus assumed has been broken by modern birth control. Many advanced nations, such as those in western Europe, are now experiencing fertility below replacement rates. Over the next century, shrinking populations may be more likely than rapidly expanding ones. There is now little reason to think that an ever-
The Kremerian Model While Malthus saw population growth as a threat to rising living standards, economist Michael Kremer has suggested that world population growth is a key driver of advancing economic prosperity. If there are more people, Kremer argues, then there are more scientists, inventors, and engineers to contribute to innovation and technological progress.
237
As evidence for this hypothesis, Kremer begins by noting that over the broad span of human history, world growth rates have increased together with world population. For example, world growth was more rapid when the world population was 1 billion (which occurred around the year 1800) than it was when the population was only 100 million (around 500 B.C.). This fact is consistent with the hypothesis that having more people induces more technological progress.
Kremer’s second, more compelling piece of evidence comes from comparing regions of the world. The melting of the polar ice caps at the end of the ice age around 10,000 B.C. flooded the land bridges and separated the world into several distinct regions that could not communicate with one another for thousands of years. If technological progress is more rapid when there are more people to discover things, then the more populous regions should have experienced more rapid growth.
And, indeed, they did. The most successful region of the world in 1500 (when Columbus reestablished technological contact) included the “Old World” civilizations of the large Eurasia–
Kremer concludes from this evidence that a large population is a prerequisite for technological advance.7