176

Every day some workers lose or quit their jobs, and some unemployed workers are hired. This perpetual ebb and flow determines the fraction of the labour force that is unemployed. In this section we develop a model of labour-force dynamics that shows what determines the natural rate of unemployment.¹

177

We start with some notation. Let L denote the labour force, E the number of employed workers, and U the number of unemployed workers. Because every worker is either employed or unemployed, the labour force is the sum of the employed and the unemployed:

L = E + U

In this notation, the rate of unemployment is U/L.

To see what factors determine the unemployment rate, we assume that the labour force L is fixed and focus on the transition of individuals in the labour force between employment and unemployment. This is illustrated in Figure 6-2. Let s denote the rate of job separation, the fraction of employed individuals who lose or leave their job each month. Let f denote the rate of job finding, the fraction of unemployed individuals who find a job each month. Together, the rate of job separation s and the rate of job finding f determine the rate of unemployment.

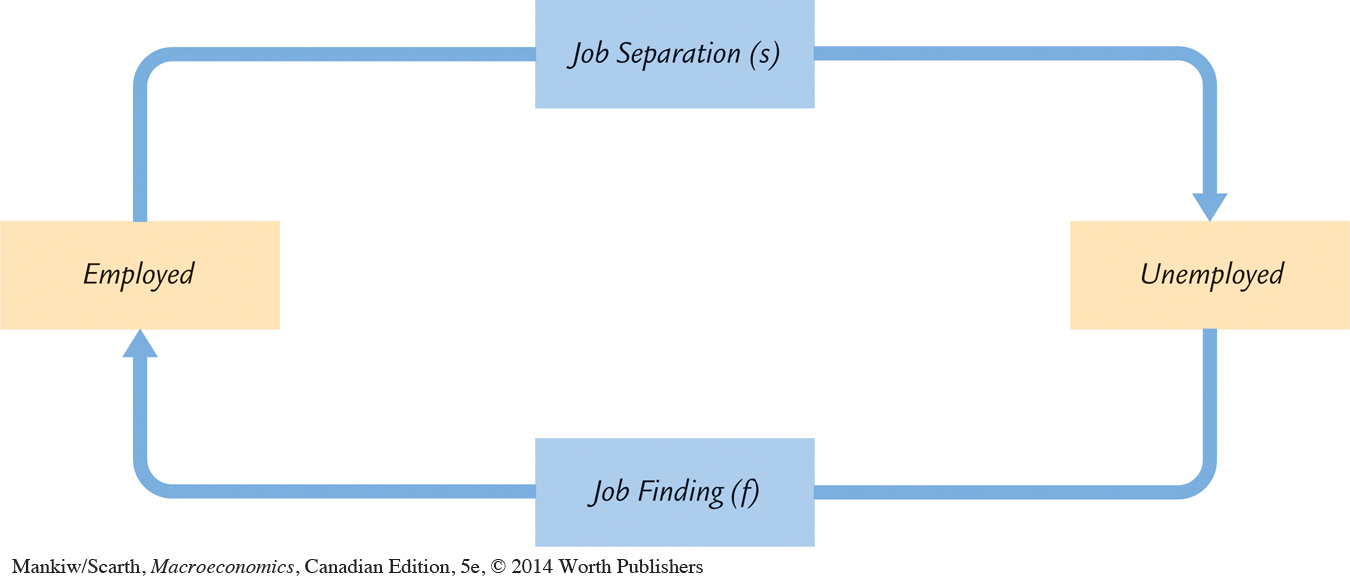
If the unemployment rate is neither rising nor falling—that is, if the labour market is in a steady state—then the number of people finding jobs must equal the number of people losing jobs. The number of people finding jobs is fU and the number of people losing jobs is sE, so we can write the steady-state condition as

fU = sE.

178

We can use this equation to find the steady-state unemployment rate. From an earlier equation, we know that E = L – U; that is, the number of employed equals the labour force minus the number of unemployed. If we substitute (L – U) for E in the steady-state condition, we find

f U = s(L – U).

Next, we divide both sides of this equation by L to obtain

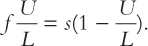
Now we can solve for U/L to find

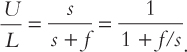
This equation shows that the steady-state rate of unemployment U/L depends on the rates of job separation s and job finding f. The higher the rate of job separation, the higher the unemployment rate. The higher the rate of job finding, the lower the unemployment rate.

Here’s a numerical example. Suppose that 1 percent of the employed lose their jobs each month (s = 0.01). This means that on average jobs last 100 months, or about 8 years. Suppose further that about 20 percent of the unemployed find a job each month (f = 0.20), so that spells of unemployment last 5 months on average. Then the steady-state rate of unemployment is

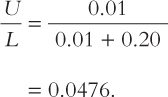
The rate of unemployment in this example is about 5 percent.

This simple model of the natural rate of unemployment has an important implication for public policy. Any policy aimed at lowering the natural rate of unemployment must either reduce the rate of job separation or increase the rate of job finding. Similarly, any policy that affects the rate of job separation or job finding also changes the natural rate of unemployment.

Although this model is useful in relating the unemployment rate to job separation and job finding, it fails to answer a central question: Why is there unemployment in the first place? If a person could always find a job quickly, then the rate of job finding would be very high and the rate of unemployment would be near zero. This model of the unemployment rate assumes that job finding is not instantaneous, but it fails to explain why. In the next two sections, we examine two underlying reasons for unemployment: job search and wage rigidity.