In a series of papers written in the 1950s, Franco Modigliani and his collaborators Albert Ando and Richard Brumberg used Fisher’s model of consumer behaviour to study the consumption function. One of their goals was to solve the consumption puzzle—that is, to explain the apparently conflicting pieces of evidence that came to light when Keynes’s consumption function was confronted with data. According to Fisher’s model, consumption depends on a person’s lifetime income. Modigliani emphasized that income varies systematically over people’s lives and that saving allows consumers to move income from those times in life when income is high to those times when it is low. This interpretation of consumer behaviour formed the basis for his life-cycle hypothesis.¹

588

One important reason that income varies over a person’s life is retirement. Most people plan to stop working at about age 65, and they expect their incomes to fall when they retire. Yet they do not want a large drop in their standard of living, as measured by their consumption. To maintain their level of consumption after retirement, people must save during their working years. Let’s see what this motive for saving implies for the consumption function.

Consider a consumer who expects to live another T years, has wealth of W, and expects to earn income Y until she retires R years from now. What level of consumption will the consumer choose if she wishes to maintain a smooth level of consumption over her life?

The consumer’s lifetime resources are composed of initial wealth W and lifetime earnings of R ∞ Y. (For simplicity, we are assuming an interest rate of zero; if the interest rate were greater than zero, we would need to take account of interest earned on savings as well.) The consumer can divide up her lifetime resources among her T remaining years of life. We assume that she wishes to achieve the smoothest possible path of consumption over her lifetime. Therefore, she divides this total of W + RY equally among the T years and each year consumes

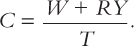
We can write this person’s consumption function as

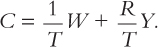
For example, if the consumer expects to live for 50 more years and work for 30 of them, then T = 50 and R =30, so her consumption function is

C = 0.02W + 0.6Y.

This equation says that consumption depends on both income and wealth. An extra $1 of income per year raises consumption by $0.60 per year, and an extra $1 of wealth raises consumption by $0.02 per year.

589

If every individual in the economy plans consumption like this, then the aggregate consumption function is much the same as the individual one. In particular, aggregate consumption depends on both wealth and income. That is, the economy’s consumption function is

C = αW + βY,

where the parameter α is the marginal propensity to consume out of wealth, and the parameter β is the marginal propensity to consume out of income.

Figure 17-10 graphs the relationship between consumption and income predicted by the life-cycle model. For any given level of wealth W, the model yields a conventional consumption function similar to the one shown in Figure 17-1. Notice, however, that the intercept of the consumption function, which shows what would happen to consumption if income ever fell to zero, is not a fixed value, as it is in Figure 17-1. Instead, the intercept here is αW and, thus, depends on the level of wealth.

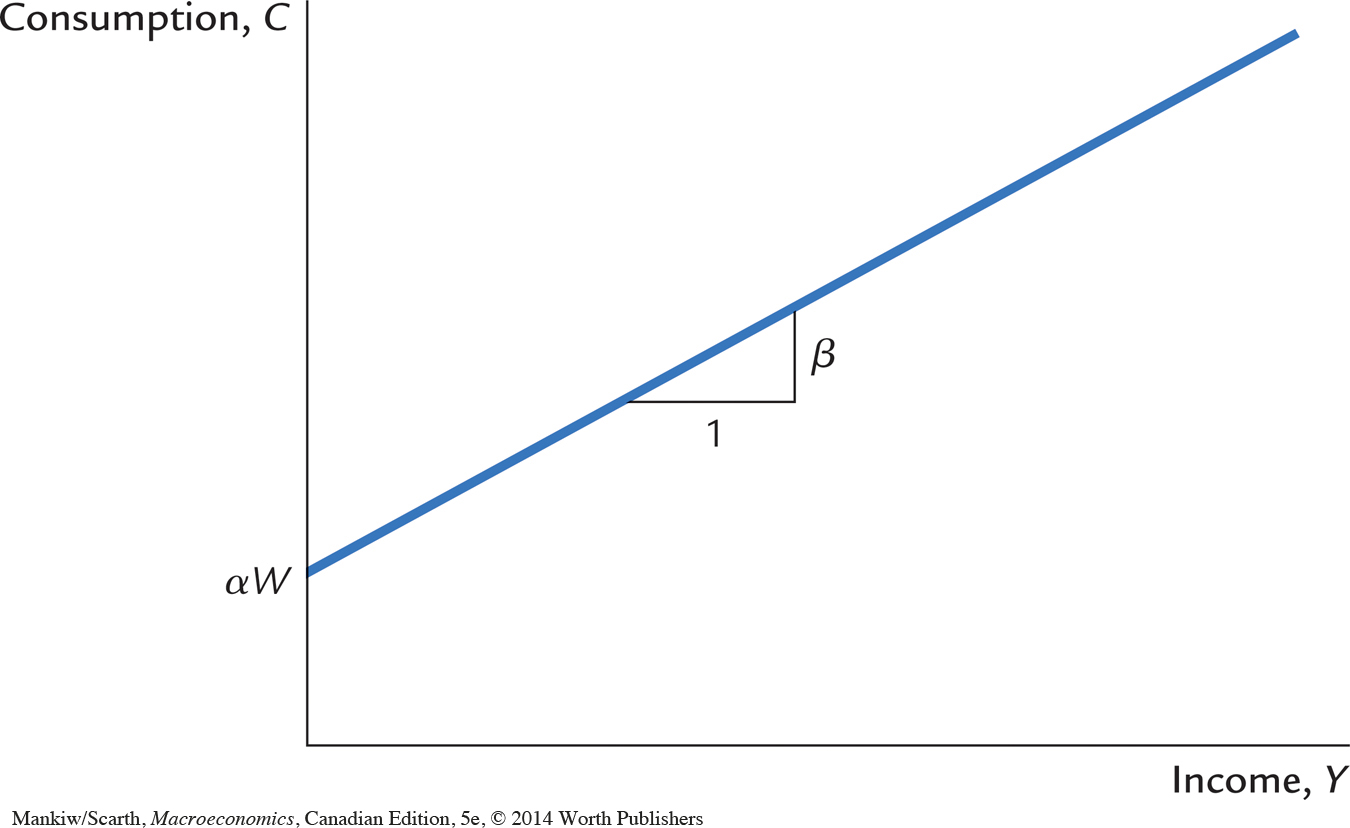
This life-cycle model of consumer behaviour can solve the consumption puzzle. According to the life-cycle consumption function, the average propensity to consume is

Because wealth does not vary proportionately with income from person to person or from year to year, we should find that high income corresponds to a low average propensity to consume when looking at data across individuals or over short periods of time. But, over long periods of time, wealth and income grow together, resulting in a constant ratio W/Y and thus a constant average propensity to consume.

590

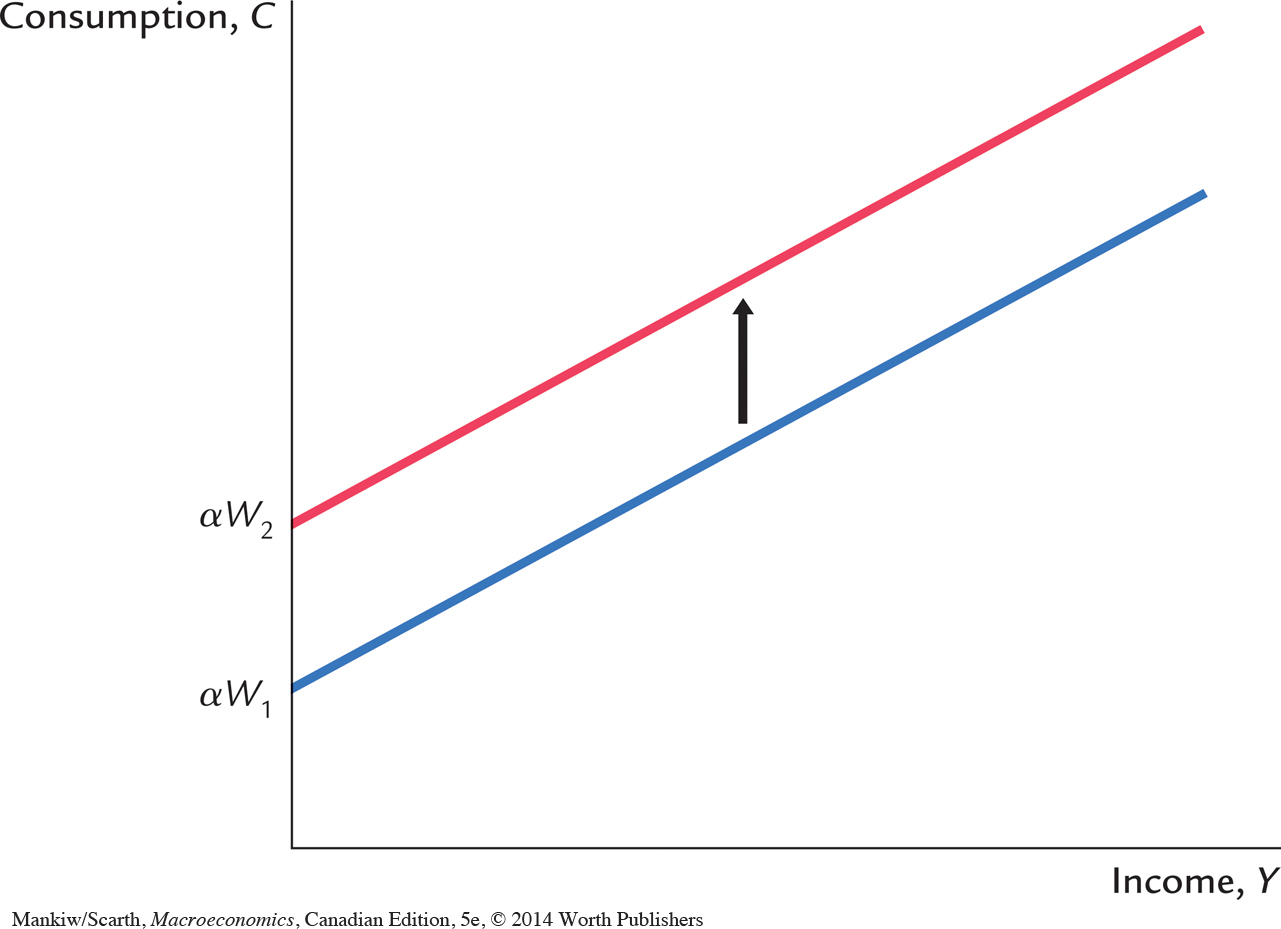
To make the same point somewhat differently, consider how the consumption function changes over time. As Figure 17-10 shows, for any given level of wealth, the life-cycle consumption function looks like the one Keynes suggested. But this function holds only in the short run when wealth is constant. In the long run, as wealth increases, the consumption function shifts upward, as in Figure 17-11. This upward shift prevents the average propensity to consume from falling as income increases. In this way, Modigliani resolved the consumption puzzle posed by Simon Kuznets’s data.

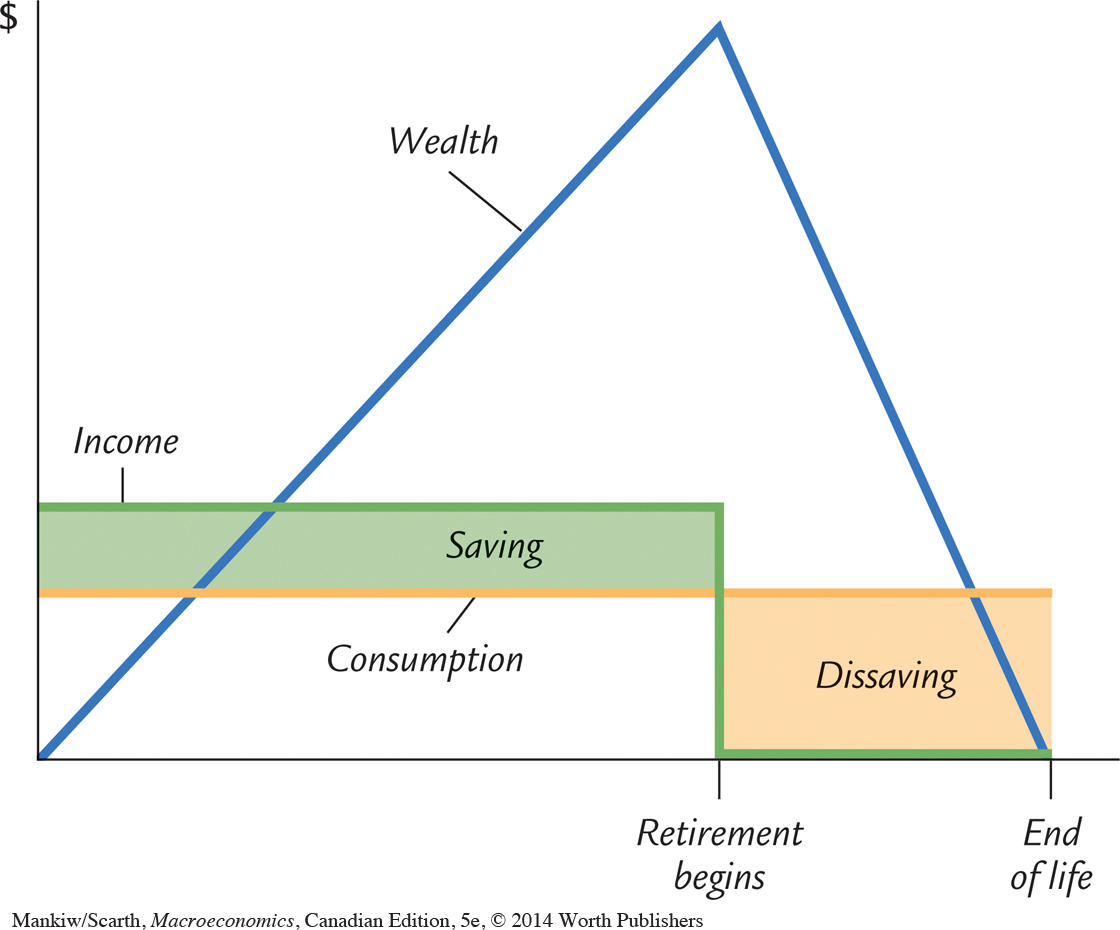
The life-cycle model makes many other predictions as well. Most important, it predicts that saving varies over a person’s lifetime. If a person begins adulthood with no wealth, she will accumulate wealth during her working years and then run down her wealth during her retirement years. Figure 17-12 illustrates the consumer’s income, consumption, and wealth over her adult life. According to the life-cycle hypothesis, because people want to smooth consumption over their lives, the young who are working save, while the old who are retired dissave.