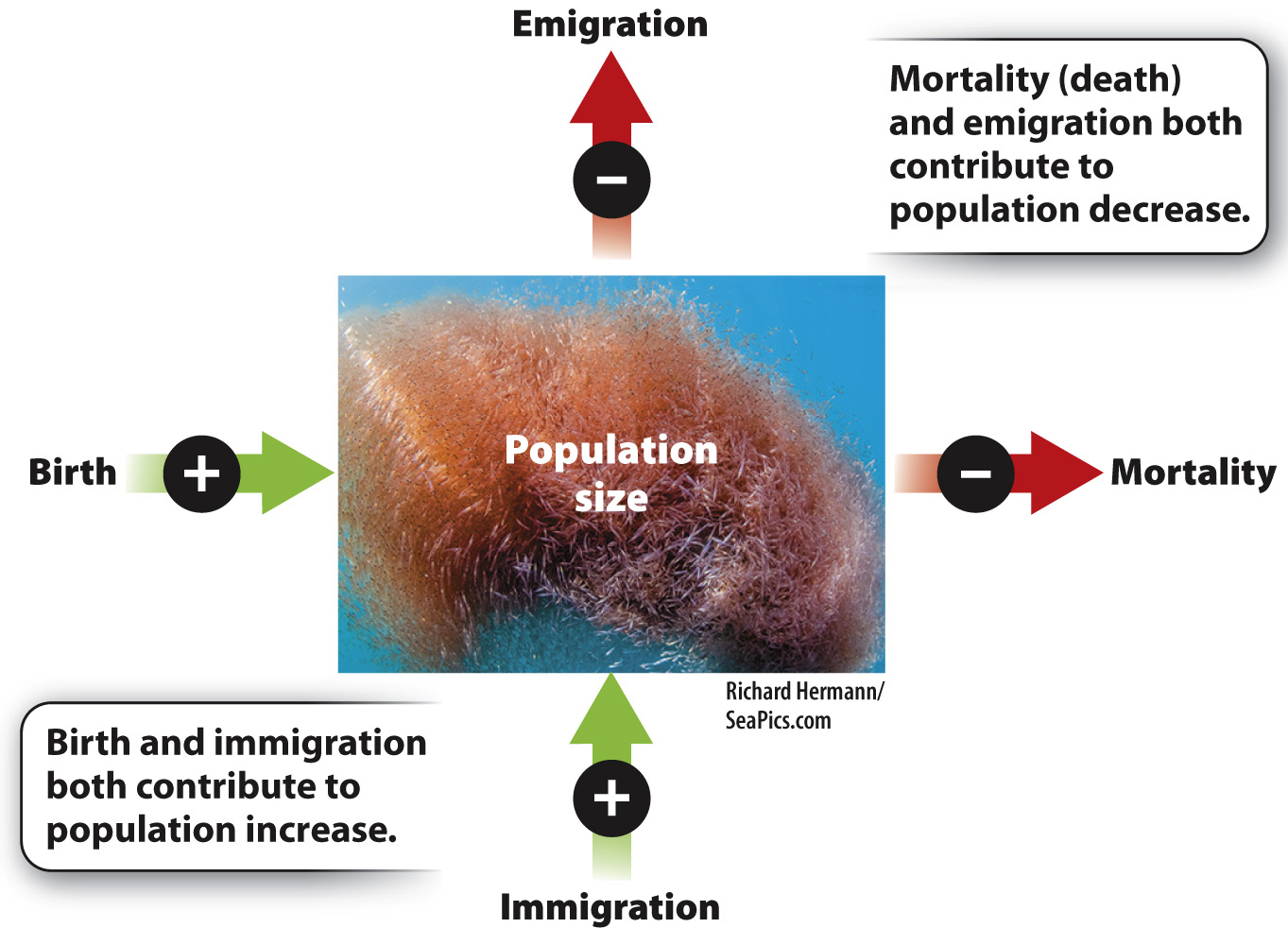
Many factors affect population size. An obvious process that contributes to population increase is birth. Another is immigration: Individuals may arrive in a population from elsewhere. In contrast, mortality (death) and emigration, the departure of individuals from a population, both act to decrease population size (Fig. 46.4).

We can describe the changes in a population’s size mathematically, defining population size as N and the change in population size over a given time interval as ΔN, where the Greek letter Δ (delta) means “change in.” ΔN is the number of individuals at a given time (time 1) minus the number of individuals at an earlier time (time 0), which is notated as N₁ – N₀. The processes leading to a change in population size through time include births (B), deaths (D), immigration (I), and emigration (E), so we can quantify ΔN as:

ΔN = N₁ – N₀ = (B – D) + (I – E)

Commonly, ecologists want to know not just whether population size is increasing or decreasing, but also the rate at which population size is changing—that is, the change in population size (ΔN) in a given period of time (Δt), or ΔN/Δt. Let’s say a population starts with 80 individuals and after 2 years has grown to 120 individuals. The population, then, has gained 40 individuals in 2 years, for a rate of 40/2 = 20 individuals per year.

The importance we place on such a number strongly depends on the actual population size. An increase of 20 individuals in a year is a big deal if the starting population had 80 individuals, but it is small if the starting population numbered 10,000. Usually, therefore, we are most interested in the proportional increase or decrease over time, especially the rate of population growth per individual, or the per capita growth rate (capita in Latin means “heads”). The average per capita growth rate is symbolized by r and is calculated as the change in population size per unit of time divided by the number of individuals at the start (time 0):

r = (ΔN/N₀)/Δt

In our example, r equals 20 individuals per year divided by 80 individuals, for an average per capita growth rate of 0.25 per year.

It is important to realize that, while rates are important in ecology, the data we usually have in hand actually consist of the numbers of individuals that we have counted, and we often do not know exactly how large a natural population really is and so must rely on estimates. In the previous section, we considered how we make such population size estimates, but for the rest of this discussion we focus on the per capita increase (or decrease) in a population over time and assume we know the population sizes for species of interest.

1008

Quick Check 1 If a population triples in size in a year, what is the per capita growth rate?