12.3 Beyond Hypothesis Testing for the One-Way Between-Groups ANOVA
Do self-
MASTERING THE CONCEPT
12.3: As with other hypothesis tests, it is recommended that we calculate an effect size in addition to conducting a hypothesis test. The most commonly reported effect size for ANOVA is R2.
R2, the Effect Size for ANOVA
R2 is the proportion of variance in the dependent variable that is accounted for by the independent variable.
In Chapter 8, we learned how to use Cohen’s d to calculate effect size. However, Cohen’s d only applies when subtracting one mean from another (as for a z test or a t test). With ANOVA, we calculate R2 (pronounced “r squared”), the proportion of variance in the dependent variable that is accounted for by the independent variable. We could also calculate a similar statistic called η2 (pronounced “eta squared”). We can interpret η2 exactly as we interpret R2.
309
MASTERING THE FORMULA
 12-
12-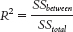 . The calculation is a ratio, similar to the calculation for the F statistic. For R2, we divide the between-
. The calculation is a ratio, similar to the calculation for the F statistic. For R2, we divide the between-
Like the F statistic, R2 is a ratio. However, it calculates the proportion of variance accounted for by the independent variable out of all of the variance. Its numerator uses only the between-
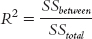
EXAMPLE 12.2
Let’s apply this to the ANOVA we just conducted. We can use the statistics in the source table we created earlier to calculate R2:
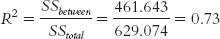
Table 12-12 displays Jacob Cohen’s conventions for R2 that, like Cohen’s d, indicate whether the effect size is small, medium, or large. This R2 of 0.73 is large. This is not surprising; if we can reject the null hypothesis when the sample size is small, then the effect size must be large. We can also turn the proportion into the more familiar language of percentages by multiplying by 100.
| Effect Size | Convention |
|---|---|
| Small | 0.01 |
| Medium | 0.06 |
| Large | 0.14 |
We can then say that a specific percentage of the variance in the dependent variable is accounted for by the independent variable. In this case, we could say that 73% of the variability in sharing is due to the type of society.
Post Hoc Tests
A post hoc test is a statistical procedure frequently carried out after the null hypothesis has been rejected in an analysis of variance; it allows us to make multiple comparisons among several means; often referred to as a follow-
The statistically significant F statistic means that some difference exists somewhere in the study. The R2 tells us that the difference is large, but we still don’t know which pairs of means are responsible for these effects. Here’s an easy way to figure it out: Graph the data. The picture will suggest which means are different, but those differences still need to be confirmed with a post hoc test. A post hoc test is a statistical procedure frequently carried out after the null hypothesis has been rejected in an analysis of variance; it allows us to make multiple comparisons among several means. The name of the test, post hoc, means “after this” in Latin; these tests are often referred to as follow-
MASTERING THE CONCEPT
12.4: ANOVA only tells us that there is a difference between at least two of the means in the study. We need a post hoc test to determine which pairs of means are statistically significantly different from each other.
For example, the fairness study produced the following mean scores: foraging, 33.25; farming, 35.0; industrial, 44.0; and natural resources, 47.333. The ANOVA told us to reject the null hypothesis, so something is going on in this data set. The Pareto chart (organized by highest to lowest) and a post hoc test will tell us “where the action is” in this statistically significant ANOVA.
310
The graph in Figure 12-5 helps us think through the possibilities. For example, people in industrial societies and in societies that extract natural resources might exhibit higher levels of fairness, on average, than people in foraging or farming societies (groups 1 and 2 versus groups 3 and 4). Or people in societies that extract natural resources might be higher, on average, only compared with those in foraging societies (group 1 versus group 4). Maybe all four groups are different from one another, on average. There are so many possibilities that we need a post hoc test to reach a statistically valid conclusion. There are many post hoc tests and most are named for their founders, almost exclusively people with fabulous names—
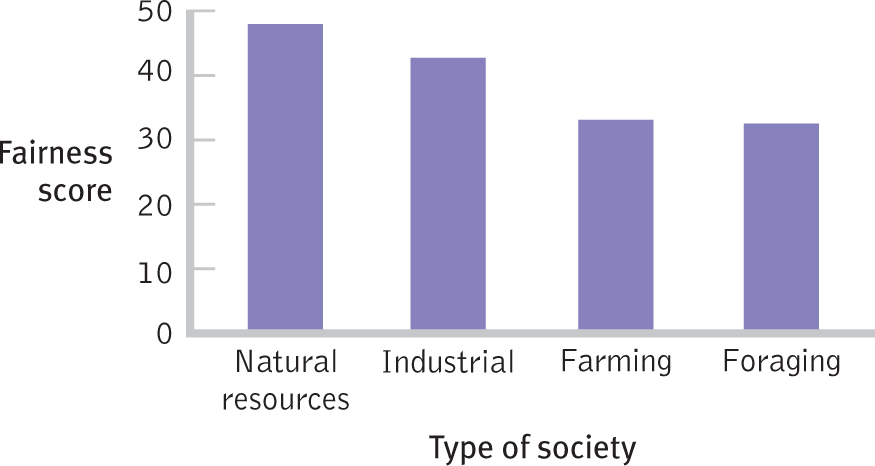
Figure 12-
Tukey HSD
The Tukey HSD test is a widely used post hoc test that determines the differences between means in terms of standard error; the HSD is compared to a critical value; sometimes called the q test.
The Tukey HSD test is a widely used post hoc test that determines the differences between means in terms of standard error; the HSD is compared to a critical value. The Tukey HSD test (also called the q test) stands for “honestly significant difference” because it allows us to make multiple comparisons to identify differences that are “honestly” there.
MASTERING THE FORMULA

 12-
12-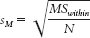 . We divide the MSwithin by the sample size and take the square root. We can then calculate the HSD for each pair of means:
. We divide the MSwithin by the sample size and take the square root. We can then calculate the HSD for each pair of means: 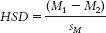 . For each pair of means, we subtract one from the other and divide by the standard error we calculated earlier.
. For each pair of means, we subtract one from the other and divide by the standard error we calculated earlier.
In the Tukey HSD test, we (1) calculate differences between each pair of means, (2) divide each difference by the standard error, and (3) compare the HSD for each pair of means to a critical value (a q value, found in Appendix B) to determine whether the means are different enough to reject the null hypothesis. The formula for the Tukey HSD test is a variant of the z test and t tests for any two sample means:
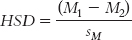
The formula for the standard error is:
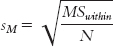
MASTERING THE FORMULA
 12-
12-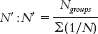 . To do that, we divide the number of groups in the study by the sum of 1 divided by the sample size for every group.
. To do that, we divide the number of groups in the study by the sum of 1 divided by the sample size for every group.
N in this case is the sample size within each group, with the assumption that all samples have the same number of participants.
When samples are different sizes, as in our example of societies, we have to calculate a weighted sample size, also known as a harmonic mean, N′ (pronounced “N prime”) before we can calculate standard error:
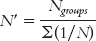
311
EXAMPLE 12.3
We calculate N′ by dividing the number of groups (the numerator) by the sum of 1 divided by the sample size for every group (the denominator). For the example in which there were four participants in foraging societies and three in each of the other three types of societies, the formula is:
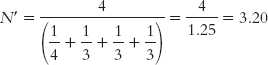
When sample sizes are not equal, we use a formula for sM based on N′ instead of N:
MASTERING THE FORMULA
12-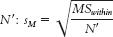 . To do that, we divide MSwithin by N′ and take the square root.
. To do that, we divide MSwithin by N′ and take the square root.
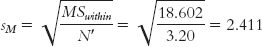
Now we use simple subtraction to calculate HSD for each pair of means. Which comes first doesn’t matter; for example, we could subtract the mean for foraging societies from the mean for farming societies, or vice versa—
Foraging (33.250) versus farming (35.000):
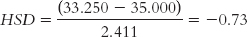
Foraging (33.250) versus natural resources (47.333):
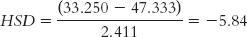
Foraging (33.250) versus industrial (44.000):
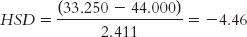
Farming (35.000) versus natural resources (47.333):
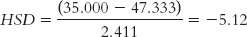
Farming (35.000) versus industrial (44.000):
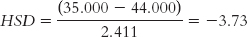
Natural resources (47.333) versus industrial (44.000):
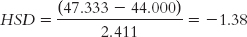
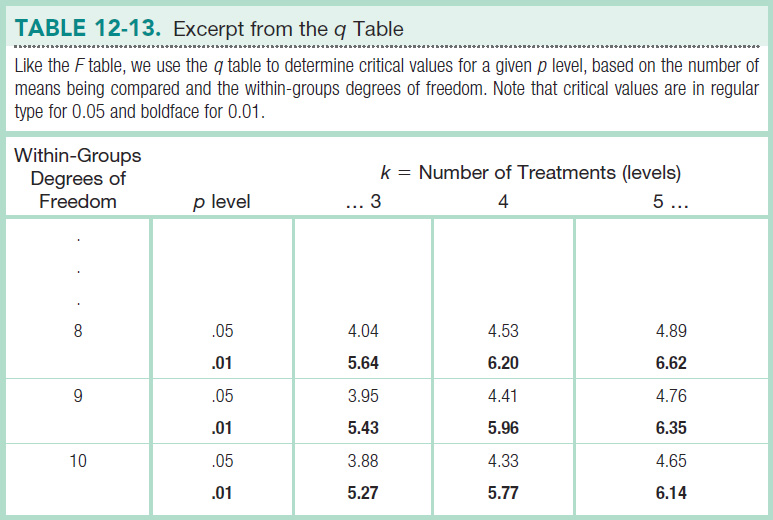
Now all we need is a critical value from the q table in Appendix B (excerpted in Table 12-13) to which we can compare the HSDs. The numbers of means being compared (levels of the independent variable) are in a row along the top of the q table, and the within-
312
The q table indicates three statistically significant differences whose HSDs are beyond the critical value of −4.41: −5.84, −4.46, and −5.12. It appears that people in foraging societies are less fair, on average, than people in societies that depend on natural resources and people in industrial societies. In addition, people in farming societies are less fair, on average, than are people in societies that depend on natural resources. We have not rejected the null hypothesis for any other pairs, so we can only conclude that there is not enough evidence to determine whether their means are different.
What might explain these differences? The researchers observed that people who purchase food routinely interact with other people in an economic market. They concluded that higher levels of market integration are associated with higher levels of fairness (Henrich et al., 2010). Social norms of fairness may develop in market societies that require cooperative interactions between people who do not know each other.
How much faith can we have in these findings? Cautious confidence and replication are recommended; researchers could not randomly assign people to live in particular societies, so some third variable may explain the relation between market integration and fairness.
Next Steps
The Bonferroni Test
For many researchers, the Tukey HSD test is the default post hoc test, and in many cases, it really is the best choice. But the wise researcher thinks about which test to choose before automatically conducting a Tukey HSD test. One other post hoc test that is often used is the Bonferroni test. It is more conservative than the Tukey HSD test, meaning that the test makes it more difficult to reject the null hypothesis. Also, the Bonferroni test is easy to implement.
313
The Bonferroni test (also sometimes called the Dunn Multiple Comparison test) is a post hoc test that provides a more strict critical value for every comparison of means.
The Bonferroni test is a post hoc test that provides a more strict critical value for every comparison of means. Normally, social scientists use a cutoff level of 0.05. With a Bonferroni test, sometimes called the Dunn Multiple Comparison test, we use a smaller critical region to make it more difficult to reject the null hypothesis. To use a Bonferroni test, we determine the number of comparisons we plan to make. Table 12-14 states the number of comparisons for two through seven means.
| Number of Means | Number of Comparisons | Bonferroni p Level (overall p = 0.05) |
|---|---|---|
| 2 | 1 | 0.05 |
| 3 | 3 | 0.017 |
| 4 | 6 | 0.008 |
| 5 | 10 | 0.005 |
| 6 | 15 | 0.003 |
| 7 | 21 | 0.002 |
The Bonferroni test is straightforward. We merely divide the p level by the number of comparisons. For a p level of 0.05 and four means, as in the fairness study, we make six comparisons using a 0.008 p level (0.05/6) for each comparison. We then conduct a series of independent-
For seven means, we would make 21 comparisons using the (0.05/21) = 0.002 p level for each comparison. The difference would have to be in the most extreme 0.2% of a t distribution before we would reject the null hypothesis!
In each case, the p levels for every comparison add up to 0.05, so we are still using a 0.05 p level overall. For example, when we make six comparisons at the 0.008 level, we have a (0.008 + 0.008 + 0.008 + 0.008 + 0.008 + 0.008) = 6(0.008) = 0.05 p level overall. Even though the overall p level remains at 0.05, the p levels for the individual comparisons rapidly become very extreme (see Table 12-14). The difference between two means must be quite extreme before we can reject the null hypothesis. We may fail to detect real differences that are not quite extreme enough, which is a Type II error.
In the fairness study, we conduct independent-
314
Unlike the Tukey HSD test, the Bonferroni test does not allow us to conclude that people in foraging societies are less fair, on average, than people in industrial societies. The test statistic is no longer beyond the critical value, because the critical value based on a Bonferroni test is more extreme than the critical value based on a Tukey HSD test.
CHECK YOUR LEARNING
Reviewing the Concepts
- As with other hypothesis tests, it is recommended that we calculate a measure of effect size when we have conducted an ANOVA. The most commonly reported effect size for ANOVA is R2.
- If we are able to reject the null hypothesis with ANOVA, we’re not finished. We must conduct a post hoc test, such as a Tukey HSD test, to determine exactly which pairs of means are significantly different from one another.
- When computing a post hoc Tukey HSD test on samples with unequal N’s, we need to calculate a weighted sample size, called N′.
- The Bonferroni test is a more conservative post hoc test than the Tukey HSD test. It makes it more difficult to reject the null hypothesis.
Clarifying the Concepts
- 12-
12 When do we conduct a post hoc test, such as a Tukey HSD test, and what does it tell us? - 12-
13 How is R2 interpreted?
Calculating the Statistics
- 12-
14 Assume that a researcher is interested in whether reaction time varies as a function of grade level. After measuring the reaction time of 10 children in fourth grade, 12 children in fifth grade, and 13 children in sixth grade, the researcher conducts an ANOVA and finds an SSbetween of 336.360 and an SStotal of 522.782. - Calculate R2.
- Write a sentence interpreting this R2. Be sure to do so in terms of the independent and dependent variables described for this study.
- 12-
15 If the researcher in Check Your Learning 12- 14 rejected the null hypothesis after performing the ANOVA and intended to perform Tukey HSD post hoc comparisons, what would the critical value of the q statistic be for the comparisons? - 12-
16 If the researcher in Check Your Learning 12- 14 were to conduct post hoc tests using the Bonferroni test, what would the adjusted p level be?
Applying the Concepts
- 12-
17 Perform Tukey HSD post hoc comparisons on the data you analyzed in Check Your Learning 12- 10. For which comparisons do you reject the null hypothesis? - 12-
18 Calculate the effect size for the data you analyzed in Check Your Learning 12- 10 and interpret its meaning.
Solutions to these Check Your Learning questions can be found in Appendix D.