18.1 Ordinal Data and Correlation

The statistical tests we discuss in this section allow researchers to draw conclusions from data that do not meet the assumptions for a parametric test, such as when the data are rank ordered. In this section, we learn how to convert scale data to ordinal data. Then we examine four tests that can be used with ordinal data: nonparametric versions of the Pearson correlation coefficient (the Spearman rank-order correlation coefficient), the paired-samples t test (the Wilcoxon signed-rank test), the independent-samples t test (the Mann–Whitney U test), and the one-way between-groups ANOVA (the Kruskal–Wallis H test).

497

When the Data Are Ordinal

National Pride University of Chicago researchers ranked 33 countries in terms of national pride. Venezuela, along with the United States, came out on top. Ordinal data such as these are analyzed using nonparametric statistics.
AP Photo/Leslie Mazoch

A 2006 University of Chicago News Office press release proclaimed, “Americans and Venezuelans Lead the World in National Pride.” Researchers from the University of Chicago’s National Opinion Research Center (NORC) surveyed citizens of 33 countries (Smith & Kim, 2006) and developed two different kinds of national pride scores: pride in specific accomplishments of their nations, like science or sports (which they called domain-specific national pride) and a more general national pride in which citizens responded to items such as, “People should support their country even if the country is in the wrong.”

So, the researchers had two sets of national pride scores— accomplishment-related and general—for each country. They converted the scores to ranks, and when results on the two scales were merged, Venezuela and the United States were tied for first place. These findings suggest many hypotheses about what creates and inflates national pride. The authors noted that countries that were settled as colonies tend to rank higher than their “mother country,” that ex-socialist countries tend to rank lower than other countries, and that countries in Asia tend to rank lower than those from other continents. The researchers also reported that there were increases in national pride among countries that had recently been subject to terrorist attacks.

Figure 18-1

A Histogram of Ordinal Data When ordinal data are graphed in a histogram, the resulting distribution is rectangular. These are data for ranks 1–10. For each rank, there is one individual. Ordinal data are never normally distributed.

We wondered about other possible precursors of national pride, such as competitiveness. Because the researchers provided ordinal data, the only way we can explore these interesting hypotheses is by using nonparametric statistics. Parametric statistics are appropriate for scale data, but they are not appropriate for ordinal data. As we noted in Chapter 17, the very nature of an ordinal variable means that it will not meet the assumptions of a scale dependent variable and a normally distributed population. As we can see in Figure 18-1, the shape of a distribution of ordinal variables is rectangular because every participant has a different rank.

Fortunately, the logic of many nonparametric statistics will be familiar to students. This is because many of the nonparametric statistical tests are specific alternatives to parametric statistical tests. These nonparametric tests may be used whenever assumptions for a parametric test are not met. In this chapter, we’ll consider four such tests (shown in Table 18-1): (1) a nonparametric equivalent for the Pearson correlation coefficient, the Spearman rank-order correlation coefficient; (2) a nonparametric equivalent for the paired-samples t test, the Wilcoxon signed-rank test; (3) a nonparametric equivalent for the independent-samples t test, the Mann–Whitney U test; (4) a nonparametric equivalent for the one-way between-groups ANOVA, the Kruskal–Wallis H test. There is almost always an established nonparametric alterative to a parametric test. When researchers can’t meet the assumptions of the parametric test they would like to conduct, they can choose the nonparametric test that is appropriate for their data.

Table : TABLE 18-1. Parametric and Nonparametric Partners Most parametric hypothesis tests have at least one equivalent nonparametric alternative. Here, all the parametric tests call for scale dependent variables, and their nonparametric counterparts all call for ordinal dependent variables.
Design Parametric Test Nonparametric Test
Association between two variables Pearson correlation coefficient Spearman rank-order correlation coefficient
Two groups; within-groups design Paired-samples t test Wilcoxon signed-rank test
Two groups; between-groups design Independent-samples t test Mann–Whitney U test
More than two groups; between-groups design One-way between-groups ANOVA Kruskal–Wallis H test

498

EXAMPLE 18.1

Nonparametric tests for ordinal data are typically used in one of two situations. First and most obviously, we use nonparametric tests when the sample data are ordinal. Second, we use nonparametric tests when the dependent variable suggests that the underlying population distribution is greatly skewed, a common situation when the sample size is small. This second reason is likely why the national pride researchers converted their data to ranks (Smith & Kim, 2006). Figure 18-2 shows a histogram of their full set of data for the variable accomplishment-related national pride— the variable that we will use for many examples in this chapter. The data appear to be positively skewed, most likely because two countries, Venezuela and the United States, appear to be outliers. Because of this, we have to transform the data from scale to ordinal.

Figure 18-2

Skewed Data The sample data for the variable, accomplishment-related national pride, are skewed. This indicates the possibility that the underlying population distribution is skewed. It is likely that the researchers chose to report their data as ranks for this reason (Smith & Kim, 2006).

It is appropriate to transform scale data to ordinal data whenever the data from a small sample are skewed. For example, look what happens to the following five data points for income when we change the data from scale to ordinal. In the first row, the one that includes the scale data, there is a severe outlier ($550,000) and the sample data suggest a skewed distribution. In the second row, the severe outlier merely becomes the last ranking. The ranked data do not have an outlier.

499

  • Scale: $24,000 $27,000 $35,000 $46,000 $550,000
  • Ordinal: 1 2 3 4 5

In the next section, we’ll transform scale data to ordinal data so that we can calculate the Spearman rank-order correlation coefficient.

The Spearman Rank-Order Correlation Coefficient

The Spearman rank-order correlation coefficient is a nonparametric statistic that quantifies the association between two ordinal variables.

Many everyday, automatic decisions are based on rank-ordered observations. For example, a person may prefer Chunky Monkey ice cream to Chubby Hubby ice cream but would not be able to specify that he liked it precisely twice as much. When we collect ranked data, we analyze it using nonparametric statistics. The Spearman rank-order correlation coefficient is a nonparametric statistic that quantifies the association between two ordinal variables.

MASTERING THE CONCEPT

18.1: We calculate a Spearman rank-order correlation coefficient to quantify the association between two ordinal variables. It is the nonparametric equivalent of the Pearson correlation coefficient.

EXAMPLE 18.2

To see how the Spearman rank-order correlation coefficient works, let’s look at a study that uses two ordinal variables, one taken from the University of Chicago study on national pride (Smith & Kim, 2006). We wondered whether accomplishment-related national pride is related to the underlying trait of competitiveness. So we randomly selected 10 countries from the university’s list and compiled those countries’ scores for accomplishment-related national pride. We also included rankings of competitiveness that had been compiled by an international business school (IMD International, 2001).

A correlation between these variables, if found, would be evidence that countries’ levels of accomplishment-related national pride are tied to levels of competitiveness. The competitiveness variable we borrowed from the business school rankings was already ordinal. However, the accomplishment-related national pride variable was initially a scale variable. When even one of the variables is ordinal, we use the Spearman rank-order correlation coefficient (often called just the Spearman correlation coefficient, or Spearman’s rho). Its symbol is almost like the one for the Pearson correlation coefficient, but it has a subscript S to indicate that it is Spearman’s correlation coefficient: rS.

To convert scale data to ordinal data, we simply organize the data from highest to lowest (or lowest to highest, if that makes more sense) and then rank them. Table 18-2 shows the conversion of accomplishment-related national pride from scale data to ordinal data. Sometimes, as seen for Austria and Canada, we have a tie. Both of these countries had an accomplishment-related national pride score of 2.40. When we rank the data, these countries take the third and fourth positions, but they must have the same rank because their scores are the same. So we take the average of the two ranks they would hold if the scores were different: (3 + 4)/2 = 3.5. Both of these countries receive the rank of 3.5.

Table : TABLE 18-2. Converting Pride Scores to Ranks When we convert scale data to ordinal data, we simply arrange the data from highest to lowest (or lowest to highest, if that makes more sense) and then rank them. These are the original data for accomplishment-related national pride. In cases of ties, we average the two ranks that these participants—countries, in this case—would hold.
Country Pride Score Pride Rank
United States 4.0 1
South Africa 2.7 2
Austria 2.4   3.5
Canada 2.4   3.5
Chile 2.3 5
Japan 1.8 6
Hungary 1.6 7
France 1.5 8
Norway 1.3 9
Slovenia 1.1 10 

Now that we have the ranks, we can compute the Spearman correlation coefficient. We first need to include both sets of ranks in the same table, as in the second and third columns in Table 18-3. We then calculate the difference (D) between each pair of ranks, as in the fourth column. The differences always add up to 0, so we must square the differences, as in the last column. As we have frequently done with squared differences in the past, we sum them—another variation on the concept of a sum of squares. The sum of these squared differences is:

500

∑D2 = (0 + 64 + 2.25 + 0.25 + 0 + 1 + 1 + 4 + 25 + 1) = 98.5

Table : TABLE 18-3. Calculating a Spearman Correlation Coefficient The first step in calculating a Spearman correlation coefficient is creating a table that includes the ranks for all participants—countries, in this case—on both variables of interest (accomplishment-related national pride and competitiveness). We then calculate differences for each participant (country, here) and square each difference.
Country Pride Rank Competitiveness
Rank		 Difference (D) Squared
Difference (D2)
United States   1   1 0 0
South Africa   2 10 −8   64  
Austria   3.5   2     1.5       2.25
Canada   3.5   3     0.5       0.25
Chile   5   5   0   0
Japan   6   7 −1   1
Hungary   7   8 −1   1
France   8   6   2   4
Norway   9   4   5 25
Slovenia 10   9   1   1

501

The formula for calculating the Spearman correlation coefficient includes the sum of the squared differences that we just calculated, 98.5. The formula is:

MASTERING THE FORMULA

18-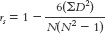1: The formula for the Spearman correlation coefficient is: . The numerator includes a constant, 6, as well as the sum of the squared differences between ranks for each participant. The denominator is calculated by multiplying the sample size, N, by the square of the sample size minus 1.

Aside from the sum of squared differences, the only other information we need is the sample size, N, which is 10 in this example. (The number 6 is a constant; it is always included in the calculation of the Spearman correlation coefficient.) The Spearman correlation coefficient, therefore, is:

The Spearman correlation coefficient is 0.40.

The interpretation of the Spearman correlation coefficient is identical to that for the Pearson correlation coefficient. The coefficient can range from −1, a perfect negative correlation, to 1, a perfect positive correlation. A correlation coefficient of 0 indicates no relation between the two variables. As with the Pearson correlation coefficient, it is not the sign of the Spearman correlation coefficient that indicates the strength of a relation. So, for example, a coefficient of −0.66 indicates a stronger association than does a coefficient of 0.23. Finally, as with the Pearson correlation coefficient, we can implement the six steps of hypothesis testing to determine whether the Spearman correlation coefficient is statistically significantly different from 0. If we do decide to conduct hypothesis testing, we can find the critical values for the Spearman correlation coefficient in Appendix B.7.

Like the Pearson correlation coefficient, the Spearman correlation coefficient does not tell us about causation. It is possible that there is a causal relation in one of two directions. The relation between competitiveness (variable A) and accomplishment-related national pride (variable B) is 0.40, a fairly strong positive correlation. It is possible that competitiveness (variable A) causes a country to feel prouder (variable B) of its accomplishments. On the other hand, it is also possible that accomplishment-related national pride (variable B) causes competitiveness (variable A). Finally, it is also possible that a third variable, C, causes both of the other two variables (A and B). For example, a high gross domestic product (variable C) might cause both a sense of competitiveness with other economic powerhouses (variable A) and a feeling of national pride at this economic accomplishment (variable B). A strong correlation indicates only a strong association; we can draw no conclusions about causation.

CHECK YOUR LEARNING

Reviewing the Concepts

  • Nonparametric statistics are used when all variables are nominal, when the dependent variable is ordinal, and when the sample suggests both that the underlying population distribution is skewed and that the sample size is small.
  • Nonparametric tests for ordinal data are used when the data are already ordinal or when it is clear that the assumptions are severely violated. In the latter case, the scale data must be converted to ordinal data.
  • When we want to calculate a correlation between two ordinal variables, we calculate a Spearman rank-order correlation coefficient, which is interpreted in the same way as a Pearson correlation coefficient.
  • As with the Pearson correlation coefficient, the Spearman correlation coefficient does not tell us about causation. It simply quantifies the magnitude and direction of association between two ordinal variables.

502

Clarifying the Concepts

  • 18-1 Describe a common situation in which we use nonparametric tests other than chi-square tests.

Calculating the Statistics

  • 18-2 Convert the following scale data to ordinal or ranked data, starting with a rank of 1 for the smallest data point.
    Observation Variable 1 Variable 2
    1 1.30 54.39
    2 1.80 50.11
    3 1.20 53.39
    4 1.06 44.89
    5 1.80 48.50
  • 18-3 Compute the Spearman correlation coefficient for the data listed in Check Your Learning 18-2.

Applying the Concepts

  • 18-4 Here are IQ scores for 10 people: 88, 90, 91, 99, 103, 103, 104, 112, 114, and 139.
    1. Why might it be better to use a nonparametric test than a parametric test in this case?
    2. Convert the scores for IQ (a scale variable) to ranks (an ordinal variable).
    3. What happens to the outlier when the scores are converted from a scale measure to an ordinal measure?

Solutions to these Check Your Learning questions can be found in Appendix D.

●
◌
◌
▣