Correlation

323

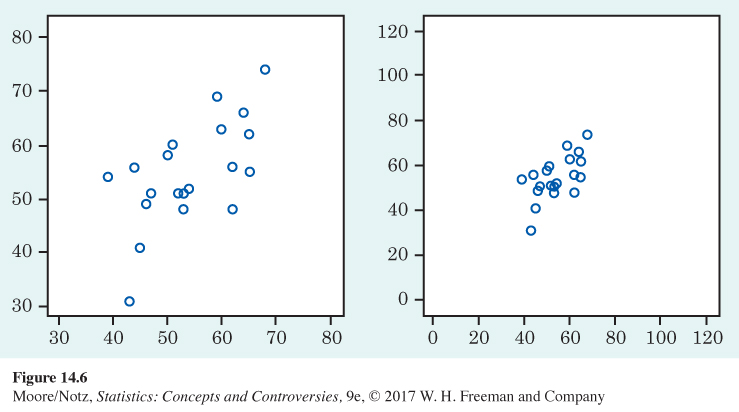
A scatterplot displays the direction, form, and strength of the relationship between two variables. Straight-line relations are particularly important because a straight line is a simple pattern that is quite common. A straight-line relation is strong if the points lie close to a straight line and weak if they are widely scattered about a line. Our eyes are not good judges of how strong a relationship is. The two scatterplots in Figure 14.6 depict the same data, but the right-hand plot is drawn smaller in a large field. The right-hand plot seems to show a stronger straight-line relationship. Our eyes can be fooled by changing the plotting scales or the amount of blank space around the cloud of points in a scatterplot. We need to follow our strategy for data analysis by using a numerical measure to supplement the graph. Correlation is the measure we use.

Correlation

The correlation describes the direction and strength of a straight-line relationship between two quantitative variables. Correlation is usually written as r.

Calculating a correlation takes a bit of work. You can usually think of r as the result of pushing a calculator button or giving a command in software and concentrate on understanding its properties and use. Knowing how we obtain r from data, however, does help us understand how correlation works, so here we go.

image
Figure 14.6: Figure 14.6 Two scatterplots of the same data. The right-hand plot suggests a stronger relationship between the variables because of the surrounding space.

324

EXAMPLE 4 Calculating correlation

We have data on two variables, x and y, for n individuals. For the fossil data in Example 3, x is femur length, y is humerus length, and we have data for n = 5 fossils.

Step 1. Find the mean and standard deviation for both x and y. For the fossil data, a calculator tells us that

Femur:
Humerus:

We use sx and sy to remind ourselves that there are two standard deviations, one for the values of x and the other for the values of y.

Step 2. Using the means and standard deviations from Step 1, find the standard scores for each x-value and for each y-value:

Value
of x 		Standard score
 Value
of y 		Standard score
38 41
56 63
59 70
64 72
74 84

Step 3. The correlation is the average of the products of these standard scores. As with the standard deviation, we “average” by dividing by n − 1, one fewer than the number of individuals:

The algebraic shorthand for the set of calculations in Example 4 is

The symbol , called “sigma,” means “add them all up.”