The Description of Data
A-
In addition to using graphs and charts, psychologists can describe their data sets using numbers that express important characteristics: measures of central tendency, measures of variation, and measures of position. These numbers are an important component of descriptive statistics, as they provide a current snapshot of a data set.
Measures of Central Tendency
measures of central tendency Numbers that represent the middle of a data set.
mean The arithmetic average of a data set; a measure of central tendency.
If you want to understand human behaviors and mental processes, it helps to know what is typical, or standard, for the population. What is the average level of intelligence? At what age do most people experience first love? To answer these types of questions, psychologists can describe their data sets by calculating measures of central tendency, which are numbers representing the “middle” of data sets. There are several ways of doing this. The mean is the arithmetic average of a data set. Most students learn how to calculate a mean, or “average,” early in their schooling, using the following formula:
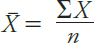 where X̄ is the sample mean; X is a value in the data set; Ʃ, or sigma, means to sum the values; and n represents the sample size
where X̄ is the sample mean; X is a value in the data set; Ʃ, or sigma, means to sum the values; and n represents the sample size
or
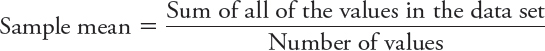
To calculate the sample mean (X̄) for minutes of REM sleep, you would plug the numbers into the formula:
X̄ = (18 + 20 + 22 + 31 + 35 + 35 + 39 + . . . + 131 + 142 + 150) ÷ 44 = 76.8 minutes
median A number that represents the position in the data set for which 50% of the values are above it, and 50% are below it; a measure of central tendency.
Another measure of central tendency is the median—the number representing the position in the middle of a data set. In other words, 50% of the data values are greater than the median, and 50% are smaller. To find the median for a small set of numbers, start by ordering the values, and then determine which number lies exactly in the center. This is relatively simple when the data set is odd-
A-
Here is how you would determine the median (Mdn) for the minutes of REM sleep:
Order the numbers in the data set from smallest to largest. We can use the stem-
and- leaf plot for this purpose. (See Figure A.3 on page A- 7.) Find the value in the data set that has 50% of the other values below it and 50% above it. Because we have an even number for our sample size (n = 44), we will have to find the middle two data values and calculate their average. We divide our sample size of 44 by 2, which is 22, indicating that the median is midway between the 22nd and 23rd values in our set. We count (starting at 18 in the stem-
and- leaf plot) to the 22nd and 23rd numbers in our ordered list (76 and 77; there are 21 values below 76 and 21 values above 77). 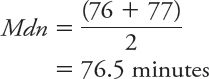
mode The value of the data set that is most frequent; a measure of central tendency.
bimodal distribution A distribution with two modes, which are the two most frequently occurring values.
A third measure of central tendency is the mode, which is the most frequently occurring value in a data set. If there is only one such value, we call it a unimodal distribution. With a symmetric distribution, the mean, median, and mode are the same (see Figure A.4a on page A-
Under other circumstances, the median is better than the mean for representing the middle of the data set. This is especially true when the data set includes one or more outliers, or values that are very different from the rest of the set. We can see why this is true by replacing just one value in our data set on REM sleep. See what happens to the mean and median when you swap 150 for 400. First calculate the mean:
X̄ = (18 + 20 + 22 + 31 + 35 + 35 + 39 + . . . + 131 + 142 + 400) ÷ 44 = 82.5 minutes (greater than the original mean of 76.8)
And now calculate the median. The numbers in the data set are ordered from smallest to largest. The middle two values have not changed (76 and 77).
Mdn = 76.5 minutes (identical to the original median of 76.5)
No matter how large (or small) a single value is, it does not change the median, but it can have a great influence on the mean. When this occurs, psychologists often present both of these statistics, and discuss the possibility that an outlier is pulling the mean toward it. Look again at the skewed distributions in Figure A.5 on page A-
Measures of Variation
measures of variation Numbers that describe the variation or dispersion in a data set.
In addition to information on the central tendency, psychologists are interested in measures of variation, which describe how much variation or dispersion there is in a data set. If you look at the two data sets in Figure A.9 below (number of miles commuting to school), you can see that they have the same central tendency (identical means: the mean commute for both samples is 30 miles; X̄ = 30.0), yet their dispersion is very different: One data set looks spread out (Sample A), and the other closely packed (Sample B).
range A number that represents the length of the data set and is a rough depiction of dispersion; a measure of variation.
There are several measures we can use to characterize the variability, or variation, of a data set. The range represents the length of a data set and is calculated by taking the highest value minus the lowest value. The range is a rough depiction of variability, but it’s useful for comparing data on the same variable measured in two samples. For the data sets presented in Figure A.9, we can compare the ranges of the two samples and see that Sample A has a range of 49 miles and Sample B has a smaller range of 25 miles.
A-

Data Values from Sample A (daily commute to school in miles) (9, 10, 15, 23, 25, 32, 35, 45, 48, 58). Data Values from Sample B (daily commute to school) (19, 27, 27, 28, 28, 30, 30, 32, 35, 44).
| Sample A | Sample B |
| Range = 58 − 9 | Range = 44 − 19 |
| Range = 49 miles | Range = 25 miles |
standard deviation A number that represents the average amount the values in a data set are away from their mean; a measure of variation.

A more precise measure of dispersion is the standard deviation (referred to by the symbol s when describing samples), which essentially represents the average amount the data points are away from their mean. Think about it like this: If the values in a data set are very close to each other, they will also be very close to their mean, and the dispersion will be small. Their average distance from the mean is small. If the values are widely spread, they will not all be clustered around the mean, and their dispersion will be great. Their average distance from the mean is large. One way we can calculate the standard deviation of a sample is by using the following formula:
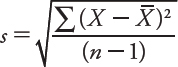
This formula does the following: (1) Subtract the mean from a value in the data set, then square the result. Do this for every value in the set and calculate the sum of the results. (2) Divide this sum by the sample size minus 1. (3) Take the square root of the result. In Table A.4, we have gone through each of these steps for Sample A.
The standard deviation for Sample A is 16.7 miles and the standard deviation for Sample B is 6.4 miles (the calculation is not shown here). These standard deviations are consistent with what we expect from looking at the stem-
The standard deviation is useful for making predictions about the probability of a particular value occurring (Figure A.4b on page A-
Measures of Position
measures of position Numbers that represent where particular data values fall in relation to other values in the data set.
Another way to describe data is by looking at measures of position, which represent where particular data values fall in relation to other values in a set. You have probably heard of percentiles, which indicate the percentage of values occurring above and below a certain point in a data set. A value at the 50th percentile is at the median, which indicates that 50% of the values fall above it, and 50% fall below it. A value at the 10th percentile indicates that 90% fall above it, and 10% fall below it. Often you will see percentiles in reports from standardized tests, weight charts, height charts, and so on.
A-
Using the data below, calculate the mean, median, range, and standard deviation. Also create a stem-
10 10 11 16 18 18 20 20 24 24 25 25 26 29 29 39 40 41 41 42 43 46 48 49 50 50 51 52 53 56 36 37 38 66 71 75 31 34 34 35 57 59 61 61 38
try this
The mean for the sample is 38.6, the median is 38, the range is 65, and the standard deviation is 16.5. A stem-