Finding a value given a proportion

true

Stat Tutor

true

You have completed 0 question sequences out of 5.

Video Player is loading.

Current Time 0:00

Duration 0:00

Loaded: 0%

Stream Type LIVE

Remaining Time -0:00

Chapters

descriptions off, selected

captions settings, opens captions settings dialog
captions off, selected

This is a modal window.

Beginning of dialog window. Escape will cancel and close the window.

TextColorTransparency

BackgroundColorTransparency

WindowColorTransparency

Font Size

Text Edge Style

Font Family

End of dialog window.

This is a modal window. This modal can be closed by pressing the Escape key or activating the close button.

This is a modal window.

Question 1

Question 1.

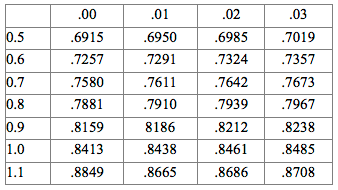
When given a cumulative proportion and asked for the corresponding z-score, how do we use the Standard Normal Table?

Look for the cumulative proportion in the center of the table and read the z-score in the margins.

Look for the z-score in the margins and find the proportion in the center of the table.

Incorrect. Cumulative proportions are found in the center of the Standard Normal table. So to find a cumulative proportion, we look in the center and read the z-score in the margins.

Correct. Cumulative proportions are found in the center of the Standard Normal table. So to find a cumulative proportion, we look in the center and read the z-score in the margins.

Incorrect. Try again.

Question 2

132

Question 2.

True or false: To find a z-score in the Standard Normal table, just look up the given proportion inside the table and read the z-score in the top row and left column.

True

False

Incorrect. Before looking up the given proportion inside the table, you must first convert it to a cumulative proportion.

Correct. Before looking up the given proportion inside the table, you must first convert it to a cumulative proportion.

Incorrect. Try again.

Questions 3-8

304

Question 3.

A z-score of -0.67 has 25% of the area less than it and 75% of the area greater than it. What do we call this value?

Median

Q₃

Q₁

Mean

Incorrect. The first quartile, Q₁, has area of 25% less than it and 75% of the area greater than it.

Correct. The first quartile, Q₁, has area of 25% less than it and 75% of the area greater than it.

Incorrect. Try again.

Question 4.

In order to find the z-score with 90% of the area to its right, what cumulative area should you look up?

0.9000

0.1000

0.0500

0.9500

Incorrect. 90% is area on the right. To get cumulative area, we subtract 90% from 100% to get 10% or 0.1000

Correct. 90% is area on the right. To get cumulative area, we subtract 90% from 100% to get 10% or 0.1000

Incorrect. Try again.

Question 5.

In order to find the z-score with 40% of the area to its left, what cumulative area should you look up?

0.8000

0.2000

0.6000

0.4000

Incorrect. 40% is area on the left, so the cumulative area is 40% or 0.4000.

Correct. 40% is area on the left, so the cumulative area is 40% or 0.4000.

Incorrect. Try again.

Question 6.

In order to find the z-scores with middle area of 60% symmetric about µ = 0, what cumulative area should you look up?

0.8000

0.2000

0.4000

0.6000

Incorrect. 100% – 60% = 40%; dividing 40% by 2 to get the area in the lower tail, we get 20% or 0.2000.

Correct. 100% – 60% = 40%; dividing 40% by 2 to get the area in the lower tail, we get 20% or 0.2000.

Incorrect. Try again.

Question 7.

Where do we locate the cumulative area in order to find a z-score?

In the inside of the table

In the right and bottom margins of the table

In the left and top margins of the table

Incorrect. Since cumulative areas are given inside the table, we locate the cumulative area and read the corresponding z-score in the left and top margins.

Correct. Since cumulative areas are given inside the table, we locate the cumulative area and read the corresponding z-score in the left and top margins.

Incorrect. Try again.

Question 8.

After we locate the cumulative area inside the Standard Normal table, where do we locate the corresponding z-score?

In the left and top margins of the table

In the right and bottom margins of the table

In the inside of the table

Incorrect. z-scores are given in the left and top margins of the table.

Correct. z-scores are given in the left and top margins of the table.

Incorrect. Try again.

Questions 9-12

379

Question 9.

True or false: Before finding a z-score for a given area, you should always convert the given area to a cumulative area if it is not already a cumulative area.

False

True

Incorrect. This is a correct statement.

Correct. This is a correct statement.

Incorrect. Try again.

Question 10.

True or false: When finding an x-value for a given area, you should find the z-score corresponding to the area in the Standard Normal table and use x = µ + zσ to find the x-value.

False

True

Incorrect. This is a correct statement.

Correct. This is a correct statement.

Incorrect. Try again.

Question 11.

Using this abbreviated Standard Normal table, what z-score has 73% of the area less than it?

0.77

0.61

0.79

0.63

0.92

0.82

Incorrect. First of all 0.73 is a cumulative area. The closest area to 0.7300 in the table is 0.7291. This corresponds to z = 0.61.

Correct. First of all 0.73 is a cumulative area. The closest area to 0.7300 in the table is 0.7291. This corresponds to z = 0.61.

Incorrect. Try again.

Question 12.

Using this abbreviated Standard Normal table, what z-score has 28% of the area greater than it?

0.77

0.82

0.63

0.92

0.79

0.60

First of all 28% is area on the right. To find the cumulative area, subtract 28% from 100% to get 72%. Looking up 0.7200, we find .7257 as the closest. This corresponds to z = 0.60.

Correct. First of all 28% is area on the right. To find the cumulative area, subtract 28% from 100% to get 72%. Looking up 0.7200, we find .7257 as the closest. This corresponds to z = 0.60.

Incorrect. Try again.

Questions 13-16

730

Question 13.

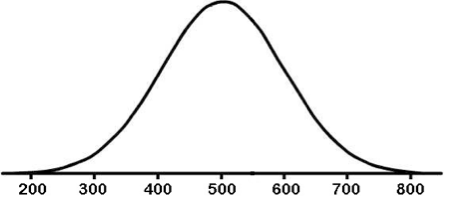
Math SAT scores are Normally distributed with mean µ = 500 and standard deviation σ = 100. Above what score are 16% of the Math SAT scores? Use the 68-95-99.7 rule.

500

400

300

700

600

Incorrect. 68% of the Math SAT scores are between 400 and 600. 100% minus 68% equals 32%. So the area below 400 plus the area above 600 equals 32%. Half of that is the area above 600. So, 16% of the scores are above 600.

Correct. 68% of the Math SAT scores are between 400 and 600. 100% minus 68% equals 32%. So the area below 400 plus the area above 600 equals 32%. Half of that is the area above 600. So, 16% of the scores are above 600.

Incorrect. Try again.

Question 14.

SAT scores for Math are Normally distributed with mean µ = 500 and standard deviation σ = 100. Below what score are 84% of the Math SAT scores? Use the 68-95-99.7 rule.

700

400

300

600

500

Incorrect. 50% of the area is less than 500. Between 500 and 600 is half of 68% or 34% of the area. 50% plus 34% = 84%. So, 84% of the scores are less than 600.

Correct. 50% of the area is less than 500. Between 500 and 600 is half of 68% or 34% of the area. 50% plus 34% = 84%. So, 84% of the scores are less than 600.

Incorrect. Try again.

Question 15.

SAT scores for Math are Normally distributed with mean µ = 500 and standard deviation σ = 100. Using the above abbreviated table, below what score are 79.1% of the Math SAT scores?

563

579

521

581

565

Incorrect. Since 79.1% of the scores are below the score of interest, we know that .7910 is a cumulative area. Looking up .7910 inside the table gives us a z-score of 0.81. We find x = µ + zσ = 500 +.81(100) = 581.

Correct. Since 79.1% of the scores are below the score of interest, we know that .7910 is a cumulative area. Looking up .7910 inside the table gives us a z-score of 0.81. We find x = µ + zσ = 500 +.81(100) = 581.

Incorrect. Try again.

Question 16.

SAT scores for Math are Normally distributed with mean µ = 500 and standard deviation σ = 100. Using the above abbreviated table, above what score are 24.2% of the Math SAT scores?

570

524

Since the z-score of 0.24 is not on this chart, the answer cannot be found.

507

604

502

Incorrect. Since 24.2% of the scores are above the score of interest, we know that .2420 the area on the right and is not a cumulative area. To get the cumulative area, we subtract .2420 from 1 to get 0.7580. Looking up .7580 inside the table gives us a z-score of 0.70. We find x = µ + zσ = 500 +.70(100) = 570.

Correct. Since 24.2% of the scores are above the score of interest, we know that .2420 the area on the right and is not a cumulative area. To get the cumulative area, we subtract .2420 from 1 to get 0.7580. Looking up .7580 inside the table gives us a z-score of 0.70. We find x = µ + zσ = 500 +.70(100) = 570.

Incorrect. Try again.

StatTutor Lesson - Finding a value given a proportion

Question 1

Question 1.

Question 2

Question 2.

Questions 3-8

Question 3.

Question 4.

Question 5.

Question 6.

Question 7.

Question 8.

Questions 9-12

Question 9.

Question 10.

Question 11.

Question 12.

Questions 13-16

Question 13.

Question 14.

Question 15.

Question 16.