Chapter 1. Continuous Probability Models
true
Stat Tutor
true
true

Question 1
2:16
Question 1.1
3DngrowsltHSp7fc9pMmgp/s5cPFoHM1avYSz6d0zZmQuktFXLZgfsKVIJWJy61Cocd+HlBMflOSCkOw54OhiTX/Sm7o0hSBOhgCdClg7IXaZTahDT9XWSXpkgYsE2SIlHJO1Ft1RoyIkptbXFhO+OvTZLvJxZgsACqlkNP+Yx3SuPnrMIckIFCwHUkBsEK1fRrcuA==Correct. Variables like height and weight are continuous. People typically round their actual weight (which can be measured in pounds, ounces, and fractions of ounces – whatever the accuracy of your scale is) to the nearest 5 or 10 pounds. Joe’s weight will not be exactly 170 pounds next Friday. The probability of Joe weighing 170 pounds will be 0.
Incorrect. Variables like height and weight are continuous. People typically round their actual weight (which can be measured in pounds, ounces, and fractions of ounces – whatever the accuracy of your scale is) to the nearest 5 or 10 pounds. Joe’s weight will not be exactly 170 pounds next Friday. The probability of Joe weighing 170 pounds will be 0.
2
Try again.
Questions 2-3
4:35
Question 1.2

Correct. The entire area under the distribution curve must be 1. This rectangle has a base of length 30; we have H x 30 = 1; solve for H.
Incorrect. The entire area under the distribution curve must be 1. This rectangle has a base of length 30; we have H x 30 = 1; solve for H.
2
Try again.
Question 1.3
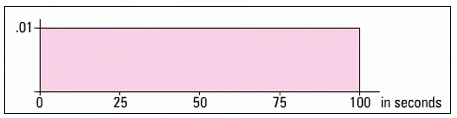
Correct. The area between 30 and 70 seconds has base (70 – 30) = 40. Multiply that times the height of 0.01.
Incorrect. The area between 30 and 70 seconds has base (70 – 30) = 40. Multiply that times the height of 0.01.
2
Try again.
Questions 4-6
6:04
Question 1.4
Q6f95HxwaOi0ia77F9AMgB0iGqPhyUF9W5hqv2lNUvemfHhGVvtFB3meaE9NO/njpjPUlylkDZU/lOgakzna/wkZvWScDQGJEYPwhanwwA1IWirmF2lrIQ==Correct. Using the standard Normal table, locate 1.5 in the left hand margin, then read the entry under the .00 column.
Incorrect. Using the standard Normal table, locate 1.5 in the left hand margin, then read the entry under the .00 column.
2
Try again.
Question 1.5
+MqaTsDBn1ahddZRSW56QDtG+MKcuShWDBi5GWV/DekbKIzTYav9+TUA/9r9jnWPxgacl5H8Uf+/dHRsCorrect. Use the standard Normal table to find P(z \(\leq\) 1.5) = 0.9332. Because the total area under the distribution curve is 1, the answer is 1 – 0.9332.
Incorrect. Use the standard Normal table to find P(z \(\leq\) 1.5) = 0.9332. Because the total area under the distribution curve is 1, the answer is 1 – 0.9332.
2
Try again.
Question 1.6
0SuFrdQi8gySWoDh8U61Hsw/ourKJ4RKlyRAwCOiNTuhVBmpx9B70ha7F9kabLttVVn/93fToHPg317ZGOXLyyFQqNk=Correct. Use the standard Normal table to find P(z \(\leq\) -1.5) = 0.0668 (or use symmetry from your previous answer). P(-1.5 < z < 1.5) = P(z > 1.5) - P(z \(\leq\) -1.5) = 0.9332 – 0.0668.
Incorrect.Use the standard Normal table to find P(z \(\leq\) -1.5) = 0.0668 (or use symmetry from your previous answer). P(-1.5 < z < 1.5) = P(z > 1.5) - P(z \(\leq\) -1.5) = 0.9332 – 0.0668.
2
Try again.
Question 7
7:23
Question 1.7
dnPMfELJcsEm008wIO5c1g/i7i4NNFDB6Dr6hX3AmBJX5oifO/MUYEcgWxnqgYl78N8dgodLlXDFLuNzHlo2M7lF0gv21LKNOd3NwWafSY64VEGM038oad1MLa6ty174hCW+rDH6tbNW/7pwi9BZ43S0VFQIsMijCh4swV1Ws3gYYB8mxIhFAsZTYCUu+QGQToRFQU/5oN7oNindI1vI0FPT7FCZIOeBFQiQtomfaI1SCK2xZoG9Gm7dU1o7xIsQwReFTVV5NjMZvOhhgTLXRne7z8bi+zKOBEZIgefAgegnbeWvPAR9I5dWyVX6mBFLqvB0QW4BRZpSUKQ9hqJUgHpl24Q=Correct. The standardized value for a 34 ounce weight is z = (34 – 34.15)/0.1 = -1.5. You already found the probability that a standard Normal random variable is less than 1.5 standard deviations below the mean.
Incorrect. The standardized value for a 34 ounce weight is z = (34 – 34.15)/0.1 = -1.5. You already found the probability that a standard Normal random variable is less than 1.5 standard deviations below the mean.
2
Try again.