Chapter 1. Tree Diagrams
true
Stat Tutor
true
true

Questions 1-4
2:09
Question 1.1
nTdVlScj80xwZS1qmUkEWHsBIv1tKeImFefBeAYv250iNNSGXRtvf6gOe3JW0OcK7IdBRuas0Ke6pkdMxmW5UpBkWoprHI+2NEZriw2EM7QeYZLQ1OVLwfinHPlaP0O6J7kJSRbEg4MDLXp9ZQW5SCJ/UnmvA84ON8wWi2SO5/9RDthbRmlBqtmlucU8boNSJ8B+poRw3rpXPeSUGvWtmU3U68YwyjHy2M8/mNKw5EWCtL6h5YhJAdogPCgHH3cIAgQrRT0yAm8K9kleaJF1ZPXlEyBJ94s2KxgtkTkCcUUq2dlEau9pXOgH9C4=Correct. If event A does not happen, we are on the lower set of branches. We can read that the probability of B happening in that case is 0.25.
Incorrect. If event A does not happen, we are on the lower set of branches. We can read that the probability of B happening in that case is 0.25.
2
Try again.
Question 1.2
DVjUB51xnx56Akakr4ECpNCGzko5lIdnQGLkl7/2s9lZngr+xO8MUFE0THSj7fefof+LCrAUEFjnbrov6RMV+S8npiHJWq+PEDeywvy22UXnW0JQr7H/p3jL/2xdkl8ots0bxjhzRTIcjgDgictf+2ovzF45/ZBwevvKu8/ruujo3fhVCPeXolueLOKxs9rP/GgyT+Qdjki1hIw7zbsSZWK0hrSjAZi5854/82kz/+1rPqRkxtagBStRIFuaSAng05RbkYl68aQKwUA5s++c2wZ97hMeqrDBO6qBOjOkpdBiwQjQ8DF76BGF2MeasnlQAcFoxa0doEc=Correct. Given that A occurs, we are on the top set of branches. In that case, we read P(B) = 0.55, so P(not B) = 1 – 0.55.
Incorrect. Given that A occurs, we are on the top set of branches. In that case, we read P(B) = 0.55, so P(not B) = 1 – 0.55.
2
Try again.
Question 1.3
TSEaPT+/aRuPJ8RsVPxqZXB7K2EjPXzuVm1lOowBBktHV98+5mDhJM57+FNzZ+0TdKCDdRRKqnN/tDXvG1IVQvEULX2OhuI7R2r0jMWFQpWKKWzort6JGzU8MIJb1cfFNFrz+7e7hga+sDRBWGM9H4FuzthzWnB8hMCEPv4W82qN4yVmYqfKQ4Gcdc0w+oo6ZUmm4Sdrkcm8bNihNkmCP4trZG33f+LdCSOGOyo18voWDquD9xpHLI1J1yUN+MfY96ZioQYfwGOpq36lqeMvQzb6dSTV6D01ljAsOIjjKAQ6dNjnqn7hn0Amn0uY2G5boMvjUGE2omvkxO1m3+/zYnyDdlzgIZ+C3SRbSeyOZAs6iisMVa863lJ1syZAQDjUNe/2NizbmJE8MxZJcYWljsPh5vxtPVodNIFfURdsgL8Bi+KSjc2W4P/z7B2BQ+BjLoLmF8ZBFOabontJwaD0BLxOBCqfh1yBpuDYOxmdY8HrynI7nHNXPpHxH/C8VWIiQ8MNPtxJQj3dV8x7hRI3MaYw5e0gcCRteHLn41lXwG3qyHrjofPDUVxTWOWA9tgYrxrcZ3Ms9Qjww651O4T3gisg1MAugqCMvxlWfMA01LQpUTIAM5i5gcKP1vTi6JY92Pd0F2AeM1APovTeHGY/ThtAtzCHd8v4vQPK6m1CSHeyt70Wz/CMssWrc9ZnLau1dJgBr55KdnZzqkGMVIWtlwC1gOlsvy0Nh7/t5qjR8mvdykPTAOOzjm096ZZA+ZKvZpxlt3wozInKGEXK60nszRJf3DUl4E78iq77vKQrCGSbSWhMylrMOR22mvX6iKIVCorrect. The 0.80 occurs on the second set of branches, so it is a conditional probability. The first event on that branch is buying a burger.
Incorrect. The 0.80 occurs on the second set of branches, so it is a conditional probability. The first event on that branch is buying a burger.
2
Try again.
Question 1.4
8XlqC7cTr/oarDt0voVuAJ51kLPsGAttC82/PdSyWFsfj4Ytf2Fn5leHN9u3n/LmSgFmAief59jq3My9Xk8axfRlIMG6qBLpEMVScw0TZqEEYcu8M3L81YUzth77/VM7tL7wBiO+Mm72jvkbXPPIJTdvbUAgXcO5kvZe2++H815PJSRqzRNPVSzg+JqLmklZnAUKifXsAgQTGVtz1P0qmmgEW9Y5BZCJVDBy6VaSk/TLRQjzjntco5OR7n4beyXyvGp8RZoQzLX0D7BJAJ7mWgYFXHOYXomnZ1QKi8dwr3wj0aCbZ3oZj1fohc6TNbFDX33DdWVNAcWFp5B/pfX0NZf6hMC7R+49jQzDkreQMCbxyYwj4S0PiJh8BDJ5jNSyoWdXu+8/SZuw/5iW3T6ejadHJfQdlHE8Ml2V6mAktlaBJ2GaTeweJjb8o0Ps4Bn5NAepL3whxn4Ik/nD8p9EGMqyUvJ/6r8d+8Vm8PVk1abX30n6F0yYqFcV9LzrX8DtO12CH3KpWT39KFVVf/tu1g5HSfIlIJEiq2d35nX6+FFKRz9JeAqCeftnY1WtGd1HyaFr0MYUuy4WTLad7TsdS1TKH6LzGmFyn42De1JRl2DdrVp2VUHtVipFbMTV6L8v0pnZFofOOYBGx3Z0TmWJaUG9AdkhSkV/RolOfNVoCuvUg2pZ1N1lUYHQ9siFHgyGxQY1WsfJo4Nc6r7BmPN/NhZJRwmH3jlRTpqieIR9sLnuIFLBwQjvRHu04B/uTXb1LTe2z3K47Zk=Correct. Each set of branches must add to 1. Because the probability of fries if a chicken sandwich is purchased is 0.50, the probability of not getting fries with the chicken sandwich is 0.50.
Incorrect. Each set of branches must add to 1. Because the probability of fries if a chicken sandwich is purchased is 0.50, the probability of not getting fries with the chicken sandwich is 0.50.
2
Try again.
Questions 5-8
3:09
Question 1.5

Correct. This is a joint probability; we find those by multiplying out the branches of the tree. Here, P(A and B) = 0.75*0.55.
Incorrect. This is a joint probability; we find those by multiplying out the branches of the tree. Here, P(A and B) = 0.75*0.55.
2
Try again.
Question 1.6
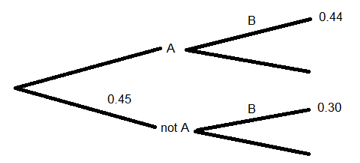
Correct. We must have P(A)*P(B | A) = 0.44. Because we were told P(not A) = 0.45, we must have P(A) = 0.55. So, we have 0.55* P(B | A) = 0.44. Solve the equation for P(B | A).
Incorrect. We must have P(A)*P(B | A) = 0.44. Because we were told P(not A) = 0.45, we must have P(A) = 0.55. So, we have 0.55* P(B | A) = 0.44. Solve the equation for P(B | A).
2
Try again.
Question 1.7
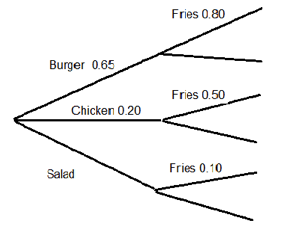
Correct. We want P(Burger and Fries). To find that probability, we multiply along that branch of the tree and have 0.65*0.80.
Incorrect. We want P(Burger and Fries). To find that probability, we multiply along that branch of the tree and have 0.65*0.80.
2
Try again.
Question 1.8
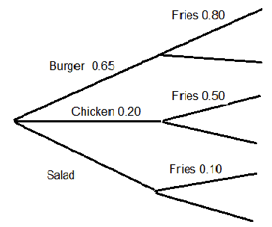
Correct. Because each set of branches must have probabilities adding to 1, we find P(Salad) = 1 − 0.65 − 0.20 = 0.15. Similarly, because P(Fries | Salad) = 0.10, we must have P(no Fries | Salad) = 0.90. Multiply 0.15*0.90 to find the probability of a salad without fries (the healthy meal).
Incorrect. Because each set of branches must have probabilities adding to 1, we find P(Salad) = 1 − 0.65 − 0.20 = 0.15. Similarly, because P(Fries | Salad) = 0.10, we must have P(no Fries | Salad) = 0.90. Multiply 0.15*0.90 to find the probability of a salad without fries (the healthy meal).
2
Try again.
Questions 9-10
6:49
Question 1.9
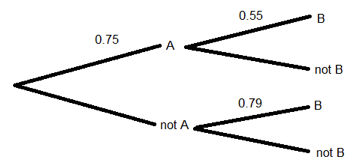
Correct. To find the probability event B happens, we need to multiply out the two branches that end with B and add those together. We have 0.75*0.55 + (1 – 0.75)*0.79.
Incorrect. To find the probability event B happens, we need to multiply out the two branches that end with B and add those together. We have 0.75*0.55 + (1 – 0.75)*0.79.
2
Try again.
Question 1.10

Correct. To find the probability a customer gets french fries, we multiply out the branches that result in no french fries and add those results together. We have 0.65*(1 – 0.80) + 0.20*(1 – 0.50) + (1 – 0.65 – 0.20)*(1 – 0.10).
Incorrect. To find the probability a customer gets french fries, we multiply out the branches that result in no french fries and add those results together. We have 0.65*(1 – 0.80) + 0.20*(1 – 0.50) + (1 – 0.65 – 0.20)*(1 – 0.10).
2
Try again.