5.2 Assess Your Understanding
Concepts and Vocabulary
Question 5.1
Explain how rectangles can be used to approximate the area enclosed by the graph of a function \(y=f(x) \geq 0\), the \(x\)-axis, and the lines \(x=a\) and \(x=b\).
Question 5.2
True or False When a closed interval \([a,b]\) is partitioned into \(n\) subintervals each of the same length, the length of each subinterval is \(\dfrac{a+b}{n}\).
Question 5.3
If the closed interval \([-2,4]\) is partitioned into \(12\) subintervals, each of the same length, then the length of each subinterval is _________.
Question 5.4
True or False If the area \(A\) under the graph of a function \(f\) that is continuous and nonnegative on a closed interval \([a,b]\) is approximated using upper sums \(S_{n}\), then \(S_{n}\geq A\) and \(A=\lim\limits_{n\rightarrow \infty }S_{n}\).
9
Skill Building
Question 5.5
Approximate the area \(A\) enclosed by the graph of \(f(x) = \dfrac{1}{2}x+3\), the \(x\)-axis, and the lines \(x=2\) and \(x=4\) by partitioning the closed interval \([2, 4]\) into four subintervals: \[ \left[ 2, \dfrac{5}{2}\right], \left[ \dfrac{5}{2},3 \right], \left[3, \dfrac{7}{2}\right], \left[ \dfrac{7}{2}, 4\right]. \]
- Using the left endpoint of each subinterval, draw four small rectangles that lie below the graph of \(f\) and sum the areas of the four rectangles.
- Using the right endpoint of each subinterval, draw four small rectangles that lie above the graph of \(f\) and sum the areas of the four rectangles.
- Compare the answers from parts (a) and (b) to the exact area \(A=9\) and to the estimates obtained in Example 1.
Question 5.6
Approximate the area \(A\) enclosed by the graph of \(f(x) =6-2x\), the \(x\)-axis, and the lines \(x=1\) and \(x=3\) by partitioning the closed interval \([ 1,3]\) into four subintervals: \[ \left[1, \dfrac{3}{2}\right], \left[ \dfrac{3}{2},2\right], \left[ 2,\dfrac{ 5}{2}\right], \left[ \dfrac{5}{2},3\right]. \]
- Using the right endpoint of each subinterval, draw four small rectangles that lie below the graph of \(f\) and sum the areas of the four rectangles.
- Using the left endpoint of each subinterval, draw four small rectangles that lie above the graph of \(f\) and sum the areas of the four rectangles.
- Compare the answers from parts (a) and (b) to the exact area \(A=4\).
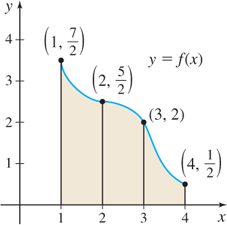
In Problems 7 and 8, refer to the illustrations. Approximate the shaded area under the graph of \(f\) from 1 to 3:
- By constructing rectangles using the left endpoint of each subinterval.
- By constructing rectangles using the right endpoint of each subinterval.
Question 5.7

Question 5.8
In Problems 9-12, partition each interval into \(n\) subintervals each of the same length.
Question 5.9
\([1,4]\) with \(n = 3\)
Question 5.10
\([0,9]\) with \(n = 9\)
Question 5.11
\([{-}1,4]\) with \(n = 10\)
Question 5.12
\([{-}4,4]\) with \(n = 16\)
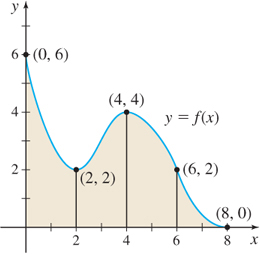
In Problems 13 and 14, refer to the graphs. Approximate the shaded area:
- By using lower sums \(s_{n}\) (rectangles that lie below the graph of \(f\)).
- By using upper sums \(S_{n}\) (rectangles that lie above the graph of \(f\)).
Question 5.13
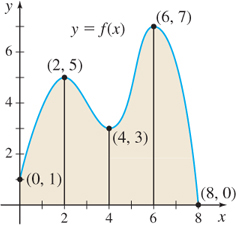
Question 5.14