Using the Law of the Sines to Solve a Triangle
Solve the triangle with side \(a=6,\) side \(b=8\), and angle \(A=35^\circ\), which is opposite side \(a.\)
Since \(a=6,\) \(b=8,\) and \(A=35 {{}^\circ},\) we have \begin{eqnarray*} \dfrac{\sin 35 {{}^\circ}}{6} &=&\dfrac{\sin B}{8} \end{eqnarray*}
A-37
\begin{eqnarray*} \sin B &=&\dfrac{8\sin 35 {{}^\circ}}{6}\approx 0.765 \end{eqnarray*} \[ B_{1}\approx 49.9 {{}^\circ}\quad\hbox{or}\quad B_{2}\approx 180 {{}^\circ}-49.9 {{}^\circ}=130.1 {{}^\circ}\]
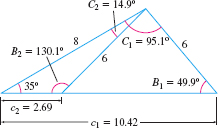
For both choices of \(B\), we have \(A+B < 180 {{}^\circ}\). So, there are two triangles, one containing the angle \(B_{1}\approx 49.9 {{}^\circ}\) and the other containing the angle \(B_{2}\approx 130.1 {{}^\circ}\). The third angle \(C\) is either \begin{eqnarray*} C_{1}&=&180^\circ-A-B_{1} \underset{\underset{\underset{\color{#0066A7}{\hbox{\({B_{1}=49.9{{}^\circ}}\)}}}{\color{#0066A7}{\hbox{\({A=35{{}^\circ}}\)}}}}{\color{#0066A7}{\displaystyle\uparrow }}}{\approx} 95.1^\circ \qquad \hbox{or}\qquad C_{2}=180^\circ-A-B \underset{\underset{\underset{\color{#0066A7}{\hbox{\({B_{2}=130.1{{}^\circ}}\)}}}{\color{#0066A7}{\hbox{\({A=35{{}^\circ}}\)}}}}{\color{#0066A7}{\displaystyle\uparrow }}} {\approx} 14.9^\circ \end{eqnarray*}
The third side \(c\) satisfies the Law of Sines, so \[ \begin{array}{rl@{\qquad}rl} \dfrac{\sin A}{a}&=\dfrac{\sin C_{1}}{c_{1}} & \dfrac{\sin A}{a}&=\dfrac{\sin C_{2}}{c_{2}} \\ \dfrac{\sin 35{{}^\circ}}{6}&=\dfrac{\sin 95.1{{}^\circ}}{c_{1}} & \dfrac{\sin 35{{}^\circ}}{6}&=\dfrac{\sin 14.9{{}^\circ}}{c_{2}} \\ c_{1}&=\dfrac{6\sin 95.1{{}^\circ}}{\sin 35{{}^\circ}}\approx 10.42 & c_{2}&=\dfrac{6\sin 14.9{{}^\circ}}{\sin 35{{}^\circ}}\approx 2.69 \end{array} \] The two solved triangles are illustrated in Figure 63.