A.2 Geometry Used in Calculus
OBJECTIVES
When you finish this section, you should be able to:
- Use properties of triangles and the Pythagorean Theorem (p. A-11)
- Work with congruent triangles and similar triangles (p. A-12)
- Use geometry formulas (p. A-15)
1 Use Properties of Triangles and the Pythagorean Theorem
A triangle is a three-sided polygon. The lengths of the sides are labeled with lowercase letters, such as \(a,\) \(b\), and \(c,\) and the angles are labeled with uppercase letters, such as \(A\), \(B\), and \(C\), with angle \( A\) opposite side \(a\), angle \(B\) opposite side \(b\), and angle \(C\) opposite side \(c\), as shown in Figure 7.

A-12
Refer to the triangle in Figure 7. The sum of the lengths of any two sides of a triangle is always greater than the length of the remaining side. The sum of the measures of the angles of a triangle, when measured in degrees, equals \(180 {{}^\circ}\). That is, \[ \begin{array}{l@{\qquad}l@{\qquad}l@{\qquad}l} a+b>c & a+c>b & b+c>a & A+B+C=180^\circ \end{array} \]
An isosceles triangle is a triangle with two equal sides. In an isosceles triangle, the angles opposite the two equal sides are equal.
An equilateral triangle is a triangle with three equal sides. In an equilateral triangle, each angle measures \(60{{}^\circ}\).
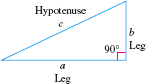
The Pythagorean Theorem is a statement about right triangles. A right triangle contains a right angle, that is, an angle measuring \(90 {{}^\circ}\). The side of the triangle opposite the \(90 {{}^\circ}\) angle is called the hypotenuse; the remaining two sides are called legs. In Figure 8, \(c\) represents the length of the hypotenuse, and \(a\) and \(b\) represent the lengths of the legs.
THEOREM Pythagorean Theorem
In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs. That is, in the right triangle shown in Figure 8, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ c^{2}=a^{2}+b^{2} }}\]
Finding the Hypotenuse of a Right Triangle
In a right triangle, one leg has length \(4\) and the other has length \(3\). What is the length of the hypotenuse?
Solution Since the triangle is a right triangle, we use the Pythagorean Theorem, with \(a=4\) and \(b=3\) to find the length \(c\) of the hypotenuse. \begin{eqnarray} c^{2} &=&a^{2}+b^{2} \nonumber \\ c^{2} &=&4^{2}+3^{2}=16+9=25 \nonumber \\ c &=&\displaystyle\sqrt{25}=5 \nonumber \end{eqnarray} The converse of the Pythagorean Theorem is also true.
THEOREM Converse of the Pythagorean Theorem
In a triangle, if the square of the length of one side equals the sum of the squares of the lengths of the other two sides, the triangle is a right triangle. The \(90 {{}^\circ}\) angle is opposite the longest side.
Using the Converse of the Pythagorean Theorem
Show that a triangle whose sides have lengths \(5\), \(12\), and \(13\) is a right triangle. Identify the hypotenuse.
Solution We square the lengths of the sides. \[ 5^{2}=25\qquad 12^{2}=144\qquad 13^{2}=169 \]
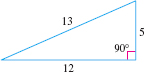
Notice that the sum of the first two squares (25 and 144) equals the third square (169). So, the triangle is a right triangle. The longest side, 13, is the hypotenuse.
See Figure 9.
2 Work with Congruent Triangles and Similar Triangles
The word congruent means “coinciding when superimposed.” For example, two angles are congruent if they have the same measure, and two line segments are congruent if they have the same length.
A-13
spanDEFINITIONspan Congruent Triangles
Two triangles are congruent if in each triangle, the corresponding angles have the same measure and the corresponding sides have the same length.
IN WORDS
Two triangles are congruent if they are the same size and shape.
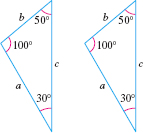
In Figure 10, corresponding angles are equal and the lengths of the corresponding sides are equal. So, these triangles are congruent.
It is not necessary to verify that all three angles and all three sides have the same measure to determine whether two triangles are congruent.
Determining Congruent Triangles
- Angle-Side-Angle Case (ASA) Two triangles are congruent if the measures of two angles from each triangle are equal and the lengths of the corresponding sides between the two equal angles are equal.
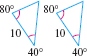
For example, in Figure 11, the two triangles are congruent because both triangles have an angle measuring \(40^\circ\), an angle measuring \(80^\circ\), and the sides between these angles are both \(10\) units in length.
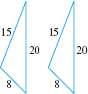
- Side-Side-Side Case (SSS) Two triangles are congruent if the lengths of the sides of one triangle are equal to the lengths of the sides of the other triangle.
For example, in Figure 12, the two triangles are congruent because both triangles have sides with lengths \(8,\) \(15,\) and \(20\) units.
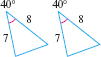
- Side-Angle-Side Case (SAS) Two triangles are congruent if the lengths of two corresponding sides of the triangles are equal and the angles between the two sides have the same measure.
For example, in Figure 13, the two triangles are congruent because both triangles have sides of length \(7\) units and \(8\) units, and the angle between the two congruent sides in each triangle measures \(40^\circ\).
- Angle-Angle-Side Case (AAS) Two triangles are congruent if the measures of two angles and the length of a nonincluded side of one triangle are equal to the corresponding parts of the other triangle.
CAUTION
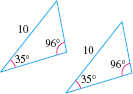
Knowing that two triangles have equal angles is not sufficient to conclude that the triangles are congruent. Similarly, knowing that the lengths of two corresponding sides and the measure of a nonincluded angle of the triangles are equal is not sufficient to conclude that the triangles are congruent.
For example, in Figure 14, the two triangles are congruent because both triangles have angles measuring \(35 {{}^\circ}\) and \(96 {{}^\circ}\), and the nonincluded side adjacent to the \(35 {{}^\circ}\) angle has length \(10\) units.
We contrast congruent triangles with similar triangles.
IN WORDS
Two triangles are similar if they have the same shape, but (possibly) different sizes.
spanDEFINITIONspan Similar Triangles
Two triangles are similar if in each triangle corresponding angles have the same measure and corresponding sides are proportional in length, that is, the ratio of the lengths of the corresponding sides of each triangle equals the same constant.
A-14
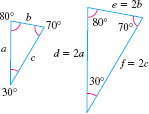
For example, the triangles in Figure 15 are similar because each of the corresponding angles of the two triangles has the same measure. Also, the lengths of the corresponding sides are proportional: each side of the triangle on the right is twice as long as the corresponding side of the triangle on the left. That is, the ratio of the corresponding sides is a constant: \(\dfrac{d}{a}=\dfrac{e}{b}=\dfrac{f}{c}=2.\)
It is not necessary to verify that all three angles are equal and all three sides are proportional to determine whether two triangles are similar.
Determining Similar Triangles
- Angle-Angle Case (AA) Two triangles are similar if the measures of two angles from each triangle are equal.
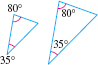
For example, the two triangles in Figure 16 are similar because each triangle has an angle measuring \(35 {{}^\circ}\) and an angle measuring \(80 {{}^\circ}\).
- Side-Side-Side Case (SSS) Two triangles are similar if the lengths of the sides of one triangle are proportional to the lengths of the sides of the second triangle.
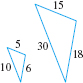
For example, Figure 17 shows two triangles with sides of lengths 5, 6, 10 and 15, 18, 30. These two triangles are similar because \[ \dfrac{5}{15}=\dfrac{6}{18}=\dfrac{10}{30}=\dfrac{1}{3} \]
- Side-Angle-Side Case (SAS) Two triangles are similar if the lengths of two sides of one triangle are proportional to the lengths of two sides of the second triangle, and the angles between the corresponding two sides have equal measure.
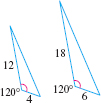
For example, in Figure 18, the two triangles are similar because \(\dfrac{4 }{6}=\dfrac{12}{18}=\dfrac{2}{3}\) and the angle between sides \(4\) and \(12\) and the angle between sides \(6\) and \(18\) each measures \(120 {{}^\circ}\).
Using Similar Triangles
Given that the triangles in Figure 19 are similar, find the missing length \( x\) and angles \(A\), \(B\), and \(C\).
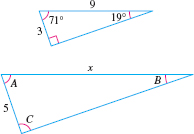
Solution Because the triangles are similar, corresponding angles have the same measure. So, \(A=71\mathbf{ {{}^\circ}}\), \(B=19\mathbf{ {{}^\circ}}\), and \(C=90\mathbf{ {{}^\circ}}\). Also corresponding sides are proportional. That is, \(\dfrac{3}{5}=\dfrac{ 9}{x}.\) We solve this equation for \(x\). \[ \begin{array}{r@{ }c@{ }l@{}l@{}l} \dfrac{3}{5} &=& \dfrac{9}{x} & & \\ 5x\cdot \dfrac{3}{5} &=& 5x\cdot \dfrac{9}{x} & & {\color{#0066A7}{\hbox{Multiply both sides by \(5x\).}}} \\ 3x&=&45 & & {\color{#0066A7}{\hbox{Simplify.}}} \\[0pt] x&=&15 & & {\color{#0066A7}{\hbox{Divide both sides by 3.}}} \end{array} \] The missing length is \(15\) units.
3 Use Geometry Formulas
A-15
Certain formulas from geometry are useful in solving calculus problems. Some of these are listed here.

For a rectangle of length \(l\) and width \(w\), \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \hbox{Area} =lw \qquad \hbox{Perimeter} =2l+2w }}\]
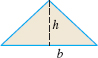
For a triangle with base \(b\) and height \(h\), \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \hbox{Area} = \dfrac{1}{2}bh }}\]
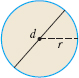
For a circle of radius \(r\) (diameter \(d=2r)\), \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \hbox{Area} =\pi r^{2}\qquad \hbox{Circumference} =2\pi r=\pi d }}\]
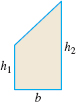
For a trapezoid with base \(b\) and parallel heights \(h_{1}\) and \(h_{2}\), \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \hbox{Area} = \dfrac{1}{2}b ( h_{1}+h_{2}) }}\]

For a closed rectangular box of length \(l,\) width \(w\), and height \(h\), \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \hbox{Volume} =lwh \qquad \hbox{Surface area} =2lh+2wh+2lw }}\]
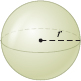
For a sphere of radius \(r\), \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \hbox{Volume} =\dfrac{4}{3}\pi r^{3}\qquad \hbox{Surface area} =4\pi r^{2} }}\]
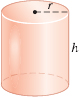
For a closed, right circular cylinder of height \(h\) and radius \(r\), \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \hbox{Volume} =\pi r^{2}h \qquad \hbox{Surface area} =2\pi r^{2}+2\pi rh }}\]
If the cylinder has no top or bottom, the surface area is \(2\pi rh.\)
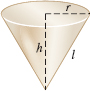
For a right circular cone of height \(h\), radius \(r\), and slant height \(l= \displaystyle\sqrt{h^{2}+r^{2}}\) that is open on top, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \hbox{Volume} = \dfrac{1}{3}\pi r^{2}h \quad \hbox{Lateral surface area} =\pi rl=\pi r\displaystyle\sqrt{h^{2}+r^{2}} }}\]
If the cone is closed on top, the surface area is \(\pi r^{2}+\pi rl\).