A.4 Trigonometry Used in Calculus
OBJECTIVES
When you finish this section, you should be able to:
- Work with angles, arc length of a circle, and circular motion (p. A-25)
- Define and evaluate trigonometric functions (p. A-27)
- Determine the domain and the range of the trigonometric functions (p. A-31)
- Use basic trigonometry identities (p. A-32)
- Use sum and difference, double-angle and half-angle, and sum-to-product and product-to-sum formulas (p. A-34)
- Solve triangles using the Law of Sines and the Law of Cosines (p. A-35)
1 Work with Angles, Arc Length of a Circle, and Circular Motion
A ray, or half-line, is the portion of a line that starts at a point \(V\) on the line and extends indefinitely in one direction. The point \(V\) of a ray is called its vertex. See Figure 43.

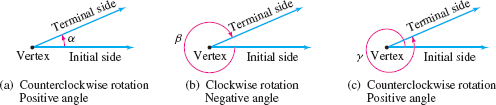
If two rays are drawn with a common vertex, they form an angle. We call one ray of an angle the initial side and the other ray the terminal side. The angle formed is identified by showing the direction and amount of rotation from the initial side to the terminal side. If the rotation is in the counterclockwise direction, the angle is positive; if the rotation is clockwise, the angle is negative. See Figure 44.
An angle \(\theta\) is in standard position if its vertex is at the origin of a rectangular coordinate system and its initial side is on the positive \(x\)-axis. See Figure 45.
A-26

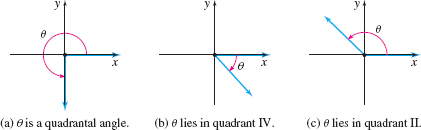
Suppose an angle \(\theta\) is in standard position. If its terminal side coincides with a coordinate axis, we say that \(\theta\) is a quadrantal angle. If its terminal side does not coincide with a coordinate axis, we say that \(\theta\) lies in a quadrant. See Figure 46.
Angles are measured by determining the amount of rotation needed for the initial side to coincide with the terminal side. The two commonly used measures for angles are degrees and radians.
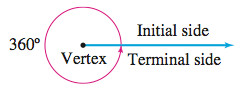
The angle formed by rotating the initial side exactly once in the counterclockwise direction until it coincides with itself (one revolution) measures \(360\) degrees, abbreviated \(360{{}^\circ}\). See Figure 47.
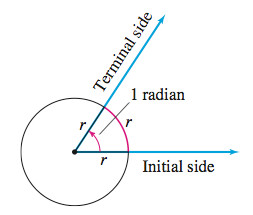
A central angle is a positive angle whose vertex is at the center of a circle. The rays of a central angle subtend (intersect) an arc on the circle. If the radius of the circle is \(r\) and the arc subtended by the central angle is also of length \(r\), then the measure of the angle is \(\mathbf{1}\) radian. See Figure 48.
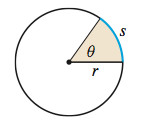
THEOREM Arc Length
For a circle of radius \(r,\) a central angle of \(\theta\) radians subtends an arc whose length \(s\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ s=r\theta }} \]
See Figure 49.
Consider a circle of radius \(r\). A central angle of one revolution will subtend an arc equal to the circumference of the circle, as shown in Figure 50. Because the circumference of a circle equals \(2\pi r\), we use \(s=2\pi r\) in the formula for arc length to find the radian measure of an angle of one revolution. \[ \begin{array}[t]{ll@{{16pt}}l} ~\ \ \ s=r\theta & & \\ 2\pi r=r\theta & & {\color{#0066A7}{\hbox{For one revolution: \(s =2\pi r\)}}}\\ ~\ \ \ \theta =2\pi \hbox{ radians} & & {\color{#0066A7}{\hbox{Solve for \(\theta\).}}} \end{array} \]
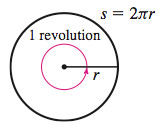
Since one revolution is equivalent to \(360 {{}^\circ}\), we have \(360 {{}^\circ}=2\pi\) radians so that \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ 180^\circ =\pi \hbox{ radians} }} \]
In calculus, radians are generally used to measure angles, unless degrees are specifically mentioned. Table 5 lists the radian and degree measures for some common angles.
A-27
Table 5
| Radians | \(0\) | \(\dfrac{\pi }{6}\) | \(\dfrac{\pi }{4}\) | \(\dfrac{\pi }{3}\) | \(\dfrac{\pi }{2}\) | \(\dfrac{2\pi }{3}\) | \(\dfrac{3\pi }{4}\) | \(\dfrac{5\pi }{6}\) | \(\pi \) | \(\dfrac{3\pi }{2}\) | \(2\pi \) |
| Degrees | \(0{{}^\circ}\) | \(30{{}^\circ}\) | \(45{{}^\circ}\) | \(60{{}^\circ}\) | \(90{{}^\circ}\) | \(120{{}^\circ}\) | \(135{{}^\circ}\) | \(150{{}^\circ}\) | \(180{{}^\circ}\) | \(270{{}^\circ}\) | \(360{{}^\circ}\) |
NOTE
If the measure of an angle is given as a number, it is understood to mean radians. If the measure of an angle is given in degrees, then it will be marked either with the symbol \({{}^\circ}\) or the word “degrees.”
THEOREM Area of a Sector
The area \(A\) of the sector of a circle of radius \(r\) formed by a central angle of \(\theta\) radians~is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ A=\dfrac{1}{2}r^{2}\theta } }\]

See Figure 51.
spanDEFINITIONspan Linear Speed, Angular Speed
Suppose an object moves around a circle of radius \(r\) at a constant speed. If \(s\) is the distance around the circle traveled in time \(t\), then the linear speed \(v\) of the object is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] {v=\dfrac{s}{t}} }\]
The angular speed \(\omega\) (the Greek letter omega) of an object moving at a constant speed around a circle of radius \(r\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \omega =\dfrac{\theta }{t}} }\]
where \(\theta\) is the angle (measured in radians) swept out in time \(t.\)
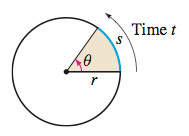
See Figure 52.
Angular speed is used to describe the turning rate of an engine. For example, an engine idling at \(900\) rpm (revolutions per minute) rotates at an angular speed of \[ 900\dfrac{\hbox{revolutions}}{\hbox{minute}}=900\dfrac{ \hbox{revolutions}}{\hbox{minute}}\cdot 2\pi \dfrac{\hbox{ radians}}{\hbox{revolution}}=1800\pi \dfrac{\hbox{ radians}}{\hbox{minute}} \]
There is an important relationship between linear speed and angular speed: \begin{eqnarray*} \hbox{linear speed }&=&v=\dfrac{s}{t}\underset{\underset{\color{#0066A7}{\hbox{\(s=r\theta\)}}}{\color{#0066A7}{\displaystyle\uparrow }}}{=}\dfrac{r\,\theta }{t}=r\left( \dfrac{\theta }{t}\right) \underset{\underset{\color{#0066A7}{\hbox{\({\omega =}\tfrac{\theta }{t}\)}}}{\color{#0066A7}{\displaystyle\uparrow }}}{=}r\omega\\ \end{eqnarray*}
RECALL
In the formula \({s=r\theta }\) for the arc length of a circle, the angle \({\theta }\) must be measured in radians.
So, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ v=r\omega }} \] where \(\omega\) is measured in radians per unit time.
When using the equation \(v=r\omega \), remember that \(v=\dfrac{s}{t}\) has the dimensions of length per unit of time (such as meters per second or miles per hour), \(r\) has the same length dimension as \(s\), and \(\omega\) has the dimensions of radians per unit of time. If the angular speed is given in terms of revolutions per unit of time (as is often the case), be sure to convert it to radians per unit of time, using the fact that one revolution \(=2\pi\) radians, before using the formula \(v=r\omega \).
2 Define and Evaluate Trigonometric Functions
There are two common approaches to trigonometry: One uses right triangles and the other uses the unit circle. We suggest you first review the approach you are most familiar with and then read the other approach. The two approaches are given below.
A-28
Right Triangle Approach
Suppose \(\theta\) is an acute angle; that is, \(0 < \theta < \dfrac{\pi }{2}\), as shown in Figure 53(a). Using the angle \(\theta \), we form a right triangle, like the one illustrated in Figure 53(b), with hypotenuse of length \(c\) and legs of lengths \(a\) and \(b.\) The three sides of the right triangle can be used to form exactly six ratios: \[ \begin{array}[t]{l@{\qquad}l@{\qquad}l@{\qquad}l@{\qquad}l@{\qquad}l} \dfrac{b}{c}, & \dfrac{a}{c}, & \dfrac{b}{a}, & \dfrac{c}{b}, & \dfrac{c}{a}, & \dfrac{a}{b} \end{array} \]
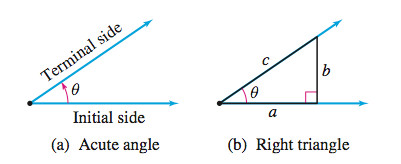
Because the ratios depend only on the angle \(\theta\) and not on the triangle itself, each ratio is given a name that involves \(\theta \). See Figure 54.

spanDEFINITIONspan Trigonometric Functions
The six ratios of a right triangle are called the trigonometric functions of an acute angle \(\theta \) and are defined as follows:
| Function name | Abbreviation | Value | Relation using words |
|---|---|---|---|
| sine of \(\theta\) | \(\sin \theta\) | \(\dfrac{b}{c}\) | \(\dfrac{\hbox{opposite}}{\hbox{hypotenuse}}\) |
| cosine of \(\theta\) | \(\cos \theta\) | \(\dfrac{a}{c}\) | \(\dfrac{\hbox{ adjacent}}{\hbox{hypotenuse}}\) |
| tangent of \(\theta\) | \(\tan \theta\) | \(\dfrac{b}{a}\) | \(\dfrac{\hbox{ opposite}}{\hbox{adjacent}}\) |
| cosecant of \(\theta\) | \(\csc \theta\) | \(\dfrac{c}{b}\) | \(\dfrac{\hbox{ hypotenuse}}{\hbox{opposite}}\) |
| secant of \(\theta\) | \(\sec \theta\) | \(\dfrac{c}{a}\) | \(\dfrac{\hbox{ hypotenuse}}{\hbox{adjacent}}\) |
| cotangent of \(\theta\) | \(\cot \theta\) | \(\dfrac{a}{b}\) | \(\dfrac{\hbox{ adjacent}}{\hbox{opposite}}\) |
To extend the definition of the trigonometric functions to include angles that are not acute, the angle is placed in standard position in a rectangular coordinate system, as shown in Figure 55.
Unit Circle Approach
Let \(t\) be any real number. We position a \(t\)-axis perpendicular to the \(x\) -axis so that \(t=0\) coincides with the point \(( 1,0)\) of the \( xy \)-plane, and positive values of \(t\) are above the \(x\)-axis. See Figure 56(a).
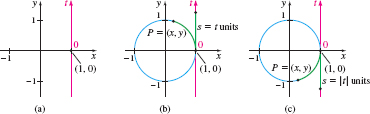
Now look at the unit circle in Figure 56(b). If \(t>0\), we begin at the point \( ( 1,0)\) on the unit circle and travel \(s=t\) units in the counterclockwise direction along the circle to arrive at the point \(P=( x, y) \). In this sense, the length \(s=t\) units on the \(t\)-axis is being wrapped around the unit circle.
If \(t<0\), we begin at the point \(( 1,0)\) on the unit circle and travel \(s=\vert \,t\vert\) units in the clockwise direction along the circle to the point \(P=( x, y) \), as shown in Figure 56(c).
If \(t>2\pi\) or if \(t<-2\pi ,\) it will be necessary to travel around the circle more than once before arriving at the point \(P\).
This discussion tells us that, for any real number \(t\), there is a unique point \(P=( x,y)\) on the unit circle, called the point on the unit circle that corresponds to \(t\). The coordinates of the point \(P=( x,y)\) are used to define the six trigonometric functions of \(t\).
spanDEFINITIONspan Trigonometric Functions of a Number \(t\)
Let \(t\) be a real number and let \(P=( x,y)\) be the point on the unit circle that corresponds to \(t\).
- The sine function is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sin t=y }}\]
- The cosine function is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \cos t=x }}\]
- If \(x\neq 0\), the tangent function is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \tan t=\dfrac{y}{x} \qquad x\neq 0}}\]
- If \(y\neq 0\), the cosecant function is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \csc t=\dfrac{1}{y} \qquad y\neq 0}} \]
- If \(x\neq 0\), the secant function is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sec t=\dfrac{1}{x} \qquad x\neq 0}}\]
- If \(y\neq 0\), the cotangent function is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \cot t=\dfrac{x}{y} \qquad y\neq 0}}\]
A-29
spanDEFINITIONspan Trigonometric Functions of \(\theta \)
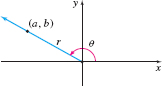
Let \(\theta\) be any angle in standard position and let \(P=( a,b)\) be any point, except the origin, on the terminal side of \(\theta \). If \(r=\displaystyle\sqrt{a^{2}+b^{2}}\) denotes the distance of the point \(P\) from the origin, then the six trigonometric functions of \(\theta \) are defined as the ratios \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{@{}c@{\qquad}c@{\qquad}c@{}} \sin \theta =\dfrac{b}{r} & \cos \theta =\dfrac{a}{r} & \tan \theta =\dfrac{b}{a} \\[8pt] \csc \theta =\dfrac{r}{b} & \sec \theta =\dfrac{r}{a} & \cot \theta =\dfrac{a}{b} \end{array} }}\] provided no denominator equals \(0.\) If a denominator equals \(0\), that trigonometric function of the angle \(\theta\) is not defined.
Notice in these definitions that, if \(x=0,\) that is, if the point \(P\) is on the \(y\)-axis, then the tangent function and the secant function are not defined. Also, if \(y=0\), that is, if the point \(P\) is on the \(x\)-axis, then the cosecant function and the cotangent function are not defined.
Because the unit circle is used in these definitions, the trigonometric functions are sometimes called circular functions.
Suppose \(\theta\) is an angle in standard position, whose terminal side is the ray from the origin through point \(P\). Since the unit circle has radius \( r=1\) unit, then, using the formula for arc length, we find that \[ s=r\theta =\theta \]
So, if \(s=\vert \,t\vert\) units, then \(\theta =t\) radians and the trigonometric functions of the angle \(\theta\) are defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{l} \sin \theta =\sin t \quad \cos \theta =\cos t \quad \tan \theta =\tan t\\[5pt] \csc \theta =\csc t \quad \sec \theta =\sec t \quad \cot \theta =\cot t \end{array} }}\]
Evaluating Trigonometric Functions
Using properties of right triangles, we can find the values of the six trigonometric functions of \(\dfrac{\pi }{6}= 30^\circ,\) \(\dfrac{\pi }{4}=45^\circ\), and \(\dfrac{\pi }{3}=60^\circ\) given in Table 6.
Table 6
| \(\theta\) (Radians) | \(\theta\) (Degrees) | \(\sin\, \theta\) | \(\cos\, \theta \) | \(\tan\, \theta \) | \(\csc\, \theta \) | \(\sec\, \theta \) | \(\cot\, \theta \) |
|---|---|---|---|---|---|---|---|
| \(\dfrac{\pi }{6}\) | \(30^\circ\) | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{3}}{3}\) | \(2\) | \(\dfrac{2\sqrt{3}}{3}\) | \(\sqrt{3}\) |
| \(\dfrac{\pi }{4}\) | \(45^\circ\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(1\) | \(\sqrt{2}\) | \(\sqrt{2}\) | 1 |
| \(\dfrac{\pi }{3}\) | \(60^\circ\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{1}{2}\) | \(\sqrt{3}\) | \(\dfrac{2\sqrt{3}}{ 3}\) | \(2\) | \(\dfrac{\sqrt{3}}{3}\) |
The values of the trigonometric functions at the quadrantal angles, \(\bigg(0=0^\circ\), \(\dfrac{\pi }{2}=90^\circ\), \(\dfrac{3\pi }{2}=270^\circ\), and \(2\pi =360^\circ\bigg)\) are given in Table 7.
Table 7
| Radians | Degrees | \(\sin\, \theta \) | \(\cos\, \theta \) | \(\tan\, \theta \) | \(\csc\, \theta \) | \(\sec\, \theta \) | \(\cot\, \theta \) |
|---|---|---|---|---|---|---|---|
| \(0\) | \(0{{}^\circ}\) | \(0\) | \(1\) | \(0\) | Not defined | \(1\) | Not defined |
| \(\dfrac{\pi }{2}\) | \(90{{}^\circ}\) | \(1\) | \(0\) | Not defined | \(1\) | Not defined | \(0\) |
| \(\pi\) | \(180{{}^\circ}\) | \(0\) | \(-1\) | \(0\) | Not defined | \(-1\) | Not defined |
| \(\dfrac{3\pi }{2}\) | \(270{{}^\circ}\) | \(-1\) | \(0\) | Not defined | \(-1\) | Not defined | \(0\) |
| \(2\pi\) | \(360{{}^\circ}\) | \(0\) | \(1\) | \(0\) | Not defined | \(1\) | Not defined |
A-30
Table 8 lists the signs of the six trigonometric functions for each quadrant.
Table 8
| Quadrant | \({\sin\, \theta,\,\csc\, \theta }\) | \({\cos\, \theta,\,\sec\, \theta }\) | \({\tan\, \theta ,\,\cot\, \theta }\) | Conclusion |
|---|---|---|---|---|
| I | Positive | Positive | Positive | All trigonometric functions are positive. |
| II | Positive | Negative | Negative | Only sine and its reciprocal, cosecant, are positive. |
| III | Negative | Negative | Positive | Only tangent and its reciprocal, cotangent, are positive. |
| IV | Negative | Positive | Negative | Only cosine and its reciprocal, secant, are positive. |
For nonacute angles \(\theta\) that lie in a quadrant, the acute angle formed by the terminal side of \(\theta\) and the \(x\)-axis, called a reference angle, is often used.
Figure 57 illustrates the reference angle for some general angles \(\theta \). Note that a reference angle is always an acute angle.

Although there are formulas for calculating reference angles, usually it is easier to find the reference angle for a given angle by making a quick sketch of the angle. The advantage of using reference angles is that, except for the correct sign, the values of the trigonometric functions of a general angle \(\theta\) equal the values of the trigonometric functions of its reference angle.
THEOREM Reference Angles
If \(\theta\) is an angle that lies in a quadrant and if \(A\) is its reference angle, then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{@{}l@{}} \sin \theta =\pm \sin A \qquad \cos \theta =\pm \cos A \qquad \tan \theta =\pm \tan A\\[4pt] \csc \theta =\pm \csc A \qquad \sec \theta =\pm \sec A \qquad \cot \theta =\pm \cot A \end{array} } }\] where the \(+\) or \(-\) sign depends on the quadrant in which \(\theta\) lies.
Using Reference Angles
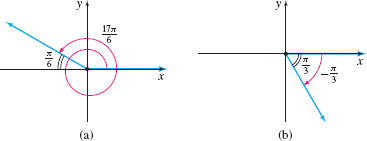
Find the exact value of: (a) \(\cos \dfrac{17\pi }{6}\)
(b) \(\tan\left( -\dfrac{\pi }{3}\right) \)
Solution (a) Refer to Figure 58(a). The angle \(\dfrac{17\pi }{6}\) is in quadrant II, where the cosine function is negative. The reference angle for \(\dfrac{17\pi }{6}\) is \(\dfrac{\pi }{6}.\) Since \(\cos \dfrac{\pi }{6}=\dfrac{\displaystyle\sqrt{3}}{2}\), \[ \cos \dfrac{17\pi }{6}=-\cos \dfrac{\pi }{6}=-\dfrac{\displaystyle\sqrt{3}}{2} \]
(b) Refer to Figure 58(b). The angle \(-\dfrac{\pi }{3}\) is in quadrant IV, where the tangent function is negative. The reference angle for \(-\dfrac{\pi }{3}\) is \(\dfrac{\pi }{3}.\) Since \(\tan \dfrac{\pi }{3}=\displaystyle\sqrt{3}\), \[ \tan \left( -\dfrac{\pi }{3}\right) =-\tan \dfrac{\pi }{3}=-\displaystyle\sqrt{3} \]
A-31
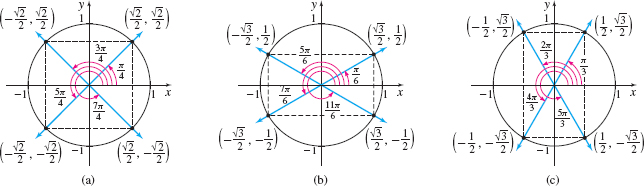
The use of symmetry provides information about integer multiples of the angles \(\dfrac{\pi }{4}=45^\circ\), \(\dfrac{\pi }{6}=30^\circ\), and \(\dfrac{\pi }{3}=60^\circ\). See the unit circles in Figure 59(a)–(c).
Finding the Exact Values of a Trigonometry Function
Use reference angles or the symmetry shown in Figure 59 to obtain:
(a) \(\sin \dfrac{7\pi }{4}=-\dfrac{\displaystyle\sqrt{2}}{2}\)
(b) \(\cos \dfrac{7\pi }{6}=-\dfrac{\displaystyle\sqrt{3}}{2}\)
(c) \(\tan \dfrac{2\pi }{3}=\dfrac{\dfrac{\displaystyle\sqrt{3}}{2}}{-\dfrac{1}{2}}=-\displaystyle\sqrt{3}\)
(d) \(\cos \left( -\dfrac{3\pi }{4}\right) =-\dfrac{\displaystyle\sqrt{2}}{2}\)
(e) \(\sin \left( -\dfrac{\pi }{6}\right) =-\dfrac{1}{2}\)
(f) \(\sin \dfrac{7\pi }{3}=\dfrac{\displaystyle\sqrt{3}}{2}\)
3 Determine the Domain and the Range of the Trigonometric Functions
Suppose \(\theta\) is an angle in standard position and \(P=( x,y)\) is the point on the unit circle corresponding to \(\theta .\) Then the six trigonometric functions are \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{@{}l@{}} \sin \theta =y \quad \,\,\, \cos \theta =x \quad \tan \theta =\dfrac{y}{x}\\[4pt] \csc \theta =\dfrac{1}{y} \quad \sec \theta =\dfrac{1}{x} \quad \cot \theta =\dfrac{x}{y} \end{array} } }\]
For \(\sin \theta\) and \(\cos \theta \), there is no concern about dividing by \(0,\) so \(\theta\) can be any angle. It follows that the domain of the sine and cosine functions is all real numbers.
- The domain of the sine function is all real numbers.
- The domain of the cosine function is all real numbers.
For the tangent and secant functions, \(x\) cannot be \(0\) since this results in division by \(0.\) On the unit circle, there are two such points, \(( 0,1)\) and \(( 0,-1)\). These two points correspond to \(\dfrac{\pi }{2}=90^\circ\) and \(\dfrac{3\pi }{2}=270^\circ\) or, more generally, to any angle that is an odd integer multiple of \(\dfrac{\pi }{2}\), such as \(\pm \dfrac{\pi }{2}=\pm 90^\circ,\) \(\pm \dfrac{3\pi }{2}=\pm 270^\circ,\) \(\pm \dfrac{5\pi }{2}=\pm 450^\circ\), and
A-32
so on. These angles must be excluded from the domain of the tangent function and the domain of the secant function.
- The domain of the tangent function is all real numbers, except odd integer multiples of \(\dfrac{\pi }{2}=90^\circ\).
- The domain of the secant function is all real numbers, except odd integer multiples of \(\dfrac{\pi }{2}=90^\circ\).
For the cotangent and cosecant functions, \(y\) cannot be \(0\) since this results in division by \(0.\) On the unit circle, there are two such points, \( ( 1,0)\) and \(( -1,0)\). These two points correspond to \(0=0 {{}^\circ}\) and \(\pi =180 {{}^\circ}\) or, more generally, to any angle that is an integer multiple of \(\pi \), such as \(0=0 {{}^\circ}\), \(\pm \pi =\pm 180 {{}^\circ},\) \(\pm 2\pi =\pm 360 {{}^\circ},\) \(\pm 3\pi =\pm 540 {{}^\circ}\), and so on. These angles must be excluded from the domain of the cotangent function and the domain of the cosecant function.
- The domain of the cotangent function is all real numbers, except integer multiples of \(\pi =180^\circ\).
- The domain of the cosecant function is all real numbers, except integer multiples of \(\pi =180^\circ\).
Now we investigate the range of the six trigonometric functions. If \(P=( x,y)\) is the point on the unit circle corresponding to the angle \(\theta\), then it follows that \(-1\leq x\leq 1\) and \(-1\leq y\leq 1.\) Since \(\sin \theta =y\) and \(\cos \theta =x,\) we have \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ -1\leq \sin \theta \leq 1\qquad \hbox{and} \qquad {-}1\leq \cos \theta \leq 1 }} \]
The range of both the sine function and the cosine function is the closed interval \([ -1,1] .\) Using absolute value notation, we have \( \vert \sin \theta \vert \leq 1\) and \(\vert \cos \theta \vert \leq 1.\)
If \(\theta\) is not an integer multiple of \(\pi =180 {{}^\circ},\) then \(\csc \theta =\dfrac{1}{y}.\) Since \(y=\sin \theta\) and \(\vert y\vert =\vert \sin \theta \vert \leq 1,\) it follows that \( \vert \csc \theta \vert =\dfrac{1}{\vert \sin \theta \vert }=\dfrac{1}{\vert y\vert }\geq 1\). That is, \(\dfrac{1 }{y}\leq -1\) or \(\dfrac{1}{y}\geq 1.\) Since \(\csc \theta =\dfrac{1}{y},\) the range of the cosecant functions consists of all real numbers in the set \(( -\infty ,-1] \cup [ 1,\infty )\). That is, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \csc \theta \leq -1\qquad \hbox{or} \qquad \csc \theta \geq 1 }}\]
If \(\theta\) is not an odd integer multiple of \(\dfrac{\pi }{2}=90 {{}^\circ},\) then \(\sec \theta =\dfrac{1}{x}.\) Since \(x=\cos \theta\) and \(\vert x\vert =\vert \cos \theta \vert \leq 1,\) it follows that \( \vert \sec \theta \vert =\dfrac{1}{\vert \cos \theta \vert }=\dfrac{1}{\vert x\vert }\geq 1\). That is, \(\dfrac{1 }{x}\leq -1\) or \(\dfrac{1}{x}\geq 1.\) Since \(\sec \theta =\dfrac{1}{x},\) the range of the secant function consists of all real numbers in the set \(( -\infty ,-1] \cup [ 1,\infty ) .\) That is, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sec \theta \leq -1 \qquad \hbox{or} \qquad \sec \theta \geq 1 }} \]
The range of both the tangent function and the cotangent function is all real numbers: \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ -\infty < \tan \theta < \infty \qquad \hbox{and} \qquad -\!\infty < \cot \theta < \infty } }\]
4 Use Basic Trigonometry Identities
spanDEFINITIONspan Identity
Two expressions \(a\) and \(b\) involving a variable \(x\) are identically equal if \[ a=b \] for every value of \(x\) for which both expressions are defined. Such an equation is referred to as an identity. An equation that is not an identity is called a conditional equation.
A-33
For example, the equation \(2x+3=x\) is a conditional equation because it is true only for \(x=-3.\) However, the equation \(x^{2}+2x=( x+1) ^{2}-1\) is true for any value of \(x,\) so it is an identity.
The basic trigonometry identities listed below are consequences of the definition of the six trigonometric functions.
Basic Trigonometry Identities
- Quotient Identities \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \tan \theta =\dfrac{\sin \theta }{\cos \theta } \qquad \qquad \cot \theta =\dfrac{\cos \theta }{\sin \theta } }}\]
- Reciprocal Identities \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \csc \theta =\dfrac{1}{\sin \theta } \qquad \sec \theta =\dfrac{ 1}{\cos \theta } \qquad \cot \theta =\dfrac{1}{\tan \theta} }}\]
- Pythagorean Identities \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sin ^{2}\theta +\cos ^{2}\theta =1 \qquad \tan ^{2}\theta +1=\sec ^{2}\theta \qquad \cot ^{2}\theta +1=\csc ^{2}\theta }}\]
- Even/Odd Identities \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \cos ( -\theta ) =\cos \theta \qquad \sin ( -\theta ) =-\sin \theta \qquad \tan ( -\theta ) =-\tan \theta }}\]
Using Basic Trigonometry Identities
(a) \(\tan \dfrac{\pi }{9}-\dfrac{\sin \dfrac{\pi }{9}}{\cos \dfrac{\pi }{9}}\underset{\underset{\color{#0066A7}{\hbox{\(\dfrac{\sin \theta }{\cos \theta }{=}\tan {\theta }\)}}}{\color{#0066A7}{\displaystyle\uparrow }}}{=} \tan \dfrac{\pi }{9}-\tan \dfrac{\pi }{9}=0\)
(b) \(\sin ^{2}\dfrac{\pi }{12}+\dfrac{1}{\sec ^{2}\dfrac{\pi }{12}}\underset{\underset{\color{#0066A7}{\hbox{\(\cos { \theta =}\frac{1}{\sec \theta}\)}}}{\color{#0066A7}{\uparrow}}}{=} \sin ^{2}\dfrac{\pi }{12}+\cos ^{2}\dfrac{\pi }{12}\underset{\underset{\color{#0066A7}{\hbox{\(\sin ^{2}{ \theta +}\cos ^{2}{ \theta =1}\)}}}{\color{#0066A7}{\uparrow}}}{=}1\)
Using Basic Trigonometry Identities
Given that \(\sin \theta =\dfrac{1}{3}\) and \(\cos \theta < 0\), find the exact value of each of the remaining five trigonometric functions.
Solution We begin by solving the identity \(\sin ^{2}\theta +\cos ^{2}\theta =1\) for \(\cos \theta \). \begin{eqnarray*} \sin ^{2}\theta +\cos ^{2}\theta &=&1 \\[3pt] \cos ^{2}\theta &=&1-\sin ^{2}\theta \\[3pt] \cos \theta &=&\pm \sqrt{1-\sin ^{2}\theta } \end{eqnarray*}
Because \(\cos \theta <0\), we choose the negative value of the radical, and use the fact that \(\sin \theta =\dfrac{1}{3}\). \begin{eqnarray*} \cos \theta &=&-\displaystyle\sqrt{1-\sin ^{2}\theta }\underset{\underset{\color{#0066A7}{\hbox{\(\sin { \theta =}\displaystyle\frac{1}{3}\)}}}{\color{#0066A7}{\displaystyle\uparrow }}}{=} -\displaystyle\sqrt{1-\frac{1}{9}}=-\displaystyle\sqrt{\dfrac{8}{9}}=-\dfrac{2\displaystyle\sqrt{2}}{3}\\ \end{eqnarray*}
A-34
The values of \(\sin \theta\) and \(\cos \theta\) are now known, so we use the quotient and reciprocal identities to obtain \[ \begin{array}{l@{\qquad}l} \tan \theta =\dfrac{\sin \theta }{\cos \theta }=\frac{\dfrac{1}{3}}{-\dfrac{2\displaystyle\sqrt{2}}{3}}=-\dfrac{1}{2 \displaystyle\sqrt{2}}=-\dfrac{\displaystyle\sqrt{2}}{4} & \cot { \theta =}\dfrac{1}{\tan \theta }{ =-2}\displaystyle\sqrt{2} \\ \sec \theta =\dfrac{1}{\cos \theta }=\frac{1}{-\dfrac{2\displaystyle\sqrt{2}}{3} }=-\dfrac{3}{2\displaystyle\sqrt{2}}=-\dfrac{3\displaystyle\sqrt{2}}{4} & \csc { \theta =}\dfrac{1}{\sin \theta }\,{ =\,}\dfrac{1}{\dfrac{1}{3}}\,{ =3} \end{array} \]
5 Use Sum and Difference, Double-Angle and Half-Angle, and Sum-to-Product and Product-to-Sum Formulas
THEOREM Sum and Difference Formulas for Sine, Cosine, and Tangent
\[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{l} {\color{#0066A7}•}\enspace \sin (A+B) =\sin A\cos B+\cos A\sin B\\[3pt] {\color{#0066A7}•}\enspace \sin (A-B) =\sin A\cos B-\cos A\sin B\\[3pt] {\color{#0066A7}•}\enspace \cos (A+B) =\cos A\cos B-\sin A\sin B\\[3pt] {\color{#0066A7}•}\enspace \cos (A-B) =\cos A\cos B+\sin A\sin B\\[3pt] {\color{#0066A7}•}\enspace \tan (A+B) =\dfrac{\tan A+\tan B}{1-\tan A\tan B}\\[5pt] {\color{#0066A7}•}\enspace \tan (A-B) =\dfrac{\tan A-\tan B}{1+\tan A\tan B} \end{array} }}\]
Using Trigonometry Identities
If \(\sin A=\dfrac{4}{5},\) \(\dfrac{\pi }{2}<A<\pi \), and \(\sin B=-\dfrac{2}{ \displaystyle\sqrt{5}}=-\dfrac{2\displaystyle\sqrt{5}}{5},\) \(\pi <B<\dfrac{3\pi }{2}\), find the exact value of:
(a) \(\cos A\)
(b) \(\cos B\)
(c) \(\cos ( A+B)\)
(d) \(\sin ( A+B) \)
Solution (a) We use a Pythagorean identity to find \(\cos A\). \begin{eqnarray*} \cos A &=&\underset{\underset{\underset{\color{#0066A7}{\hbox{\(\cos A{ <0}\)}}}{\color{#0066A7}{\hbox{ A is in quadrant II}}}} {\color{#0066A7}{\displaystyle\uparrow }}}{} -\displaystyle\sqrt{1-\sin ^{2}A}=-\displaystyle\sqrt{1-\left( \dfrac{4}{5}\right) ^{2}}=-\displaystyle\sqrt{1-\dfrac{16}{25}}=-\displaystyle\sqrt{\dfrac{9}{25}}=- \dfrac{3}{5}\\ \end{eqnarray*}
(b) We also find \(\cos B\) using a Pythagorean identity. \[ \cos B=-\displaystyle\sqrt{1-\sin ^{2}B}=-\displaystyle\sqrt{1-\dfrac{4}{5}}=-\displaystyle\sqrt{\dfrac{1}{5}}=- \dfrac{\displaystyle\sqrt{5}}{5} \]
(c) We use the results from (a) and (b) and a sum formula to find \(\cos ( A+B) \). \begin{eqnarray*} \cos ( A+B) &=&\cos A\cos B-\sin A\sin B \\[4pt] &=&\left( -\dfrac{3}{5}\right) \left( -\dfrac{\displaystyle\sqrt{5}}{5}\right) -\left( \dfrac{4}{5}\right) \left( -\dfrac{2\displaystyle\sqrt{5}}{5}\right) =\dfrac{11\displaystyle\sqrt{5}}{ 25} \end{eqnarray*}
(d) We use a sum formula to find \(\sin (A+B) \). \[ \sin ( A+B) =\sin A\cos B+\cos A\sin B=\left(\! \dfrac{4}{5}\!\right) \left(\! -\dfrac{\displaystyle\sqrt{5}}{5}\!\right) +\left(\! -\dfrac{3}{5}\!\right) \left(\! - \dfrac{2\displaystyle\sqrt{5}}{5}\!\right) =\dfrac{2\displaystyle\sqrt{5}}{25} \]
A-35
THEOREM Double-Angle Formulas
- \(\sin ( 2\theta ) =2\sin \theta \cos \theta\)
- \(\cos ( 2\theta ) =\cos ^{2}\theta -\sin ^{2}\theta\)
- \(\tan ( 2\theta ) =\dfrac{2\tan \theta }{1-\tan ^{2}\theta }\)
- \(\cos ( 2\theta ) =1-2\sin ^{2}\theta\)
- \(\cos ( 2\theta ) =2\cos ^{2}\theta -1\)
The double-angle formulas in the first row are derived directly from the sum formulas by letting \(\theta =A=B.\) A Pythagorean identity is used to obtain those in the second row.
By rearranging the double-angle formulas, other identities can be obtained that are used in calculus. \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ {\color{#0066A7}•}\enspace \sin ^{2}\theta =\dfrac{1-\cos ( 2\theta ) }{2} \qquad {\color{#0066A7}•}\enspace \cos ^{2}\theta = \dfrac{1+\cos ( 2\theta ) }{2} } }\]
If, in the double-angle formulas, we replace \(\theta\) with \(\dfrac{1}{2} \theta ,\) we obtain these identities. \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ {\color{#0066A7}•}\enspace \sin ^{2}\dfrac{\theta }{2}=\dfrac{1-\cos \theta }{2} \qquad {\color{#0066A7}•}\enspace \cos ^{2}\dfrac{\theta }{2}=\dfrac{1+\cos \theta }{2} \qquad {\color{#0066A7}•}\enspace \tan ^{2} \dfrac{\theta }{2}=\dfrac{1-\cos \theta }{1+\cos \theta } } }\]
Taking the square root produces the half-angle formulas. \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ {\color{#0066A7}•}\enspace \sin \dfrac{\theta }{2}=\pm \displaystyle\sqrt{\dfrac{1-\cos \theta }{2}} \quad {\color{#0066A7}•}\enspace \cos \dfrac{\theta }{2}=\pm \displaystyle\sqrt{\dfrac{ 1+\cos \theta }{2}} \quad {\color{#0066A7}•}\enspace \tan \dfrac{\theta }{2}=\pm \displaystyle\sqrt{\dfrac{1-\cos \theta }{1+\cos \theta }} } }\]
where the \(+\) or \(-\) sign is determined by the quadrant of the angle \(\dfrac{ \theta }{2}\).
The product-to-sum and sum-to-product identities are also used in calculus. They are a result of combining the sum and difference formulas. \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ {\color{#0066A7}•}\enspace \sin A\,\cos B=\dfrac{1}{2} [ \sin (A+B) +\sin ( A-B) ] }}\] \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ {\color{#0066A7}•}\enspace \cos A\,\cos B=\dfrac{1}{2}[ \cos ( A+B) +\cos( A-B) ] }}\] \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ {\color{#0066A7}•}\enspace \sin B\sin B=\dfrac{1}{2} [ \cos ( A-B) -\cos ( A+B) ] }}\]
6 Solve Triangles Using the Law of Sines and the Law of Cosines
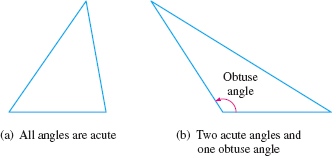
If no angle of a triangle is a right angle, the triangle is called oblique. An oblique triangle either has three acute angles or two acute angles and one obtuse angle (an angle between \(\dfrac{\pi }{2}\) and \(\pi \)). See Figure 60.
A-36
NOTE
To solve an oblique triangle, you must know the length of at least one side. Knowing only angles results in a family of similar triangles.
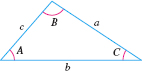
In the discussion that follows, we label an oblique triangle so that side \(a\) is opposite angle \(A\), side \(b\) is opposite angle \(B\), and side \(c\) is opposite angle \(C\), as shown in Figure 61.
To solve an oblique triangle means to find the lengths of its sides and the measures of its angles. To do this, we need to know the length of one side along with (i) two angles; (ii) one angle and one other side; or (iii) the other two sides. There are four possibilities to consider:
- Case 1: One side and two angles are known (ASA or SAA).
- Case 2: Two sides and the angle opposite one of them are known (SSA).
- Case 3: Two sides and the included angle are known (SAS).
- Case 4: Three sides are known (SSS).
Figure 62 illustrates the four cases.

The Law of Sines is used to solve triangles for which Case 1 or 2 holds.
THEOREM Law of Sines
For a triangle with sides \(a\), \(b\), \(c\) and opposite angles \(A\), \(B\), \(C\), respectively, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} }}\]
The Law of Sines actually consists of three equalities: \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \dfrac{\sin A}{a}=\dfrac{\sin B}{b} \qquad \dfrac{\sin A}{a}=\dfrac{\sin C}{c} \qquad \dfrac{\sin B}{b}=\dfrac{\sin C}{c} }}\]
Formula (1) is a compact way to write these three equations.
For Case 1 (ASA or SAA), two angles are given. The third angle can be found using the fact that the sum of the angles in a triangle measures \(180 {{}^\circ}\). Then use the Law of Sines (twice) to find the two missing sides.
Case 2 (SSA), which applies to triangles for which two sides and the angle opposite one of them are known, is referred to as the ambiguous case , because the information can result in one triangle, two triangles, or no triangle at all.
Using the Law of the Sines to Solve a Triangle
Solve the triangle with side \(a=6,\) side \(b=8\), and angle \(A=35^\circ\), which is opposite side \(a.\)
Solution Because two sides and an opposite angle are known (SSA), we use the Law of Sines to find angle \(B\). \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b} \]
Since \(a=6,\) \(b=8,\) and \(A=35 {{}^\circ},\) we have \begin{eqnarray*} \dfrac{\sin 35 {{}^\circ}}{6} &=&\dfrac{\sin B}{8} \end{eqnarray*}
A-37
\begin{eqnarray*} \sin B &=&\dfrac{8\sin 35 {{}^\circ}}{6}\approx 0.765 \end{eqnarray*} \[ B_{1}\approx 49.9 {{}^\circ}\quad\hbox{or}\quad B_{2}\approx 180 {{}^\circ}-49.9 {{}^\circ}=130.1 {{}^\circ}\]
For both choices of \(B\), we have \(A+B < 180 {{}^\circ}\). So, there are two triangles, one containing the angle \(B_{1}\approx 49.9 {{}^\circ}\) and the other containing the angle \(B_{2}\approx 130.1 {{}^\circ}\). The third angle \(C\) is either \begin{eqnarray*} C_{1}&=&180^\circ-A-B_{1} \underset{\underset{\underset{\color{#0066A7}{\hbox{\({B_{1}=49.9{{}^\circ}}\)}}}{\color{#0066A7}{\hbox{\({A=35{{}^\circ}}\)}}}}{\color{#0066A7}{\displaystyle\uparrow }}}{\approx} 95.1^\circ \qquad \hbox{or}\qquad C_{2}=180^\circ-A-B \underset{\underset{\underset{\color{#0066A7}{\hbox{\({B_{2}=130.1{{}^\circ}}\)}}}{\color{#0066A7}{\hbox{\({A=35{{}^\circ}}\)}}}}{\color{#0066A7}{\displaystyle\uparrow }}} {\approx} 14.9^\circ \end{eqnarray*}
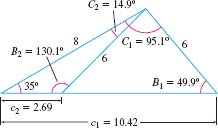
The third side \(c\) satisfies the Law of Sines, so \[ \begin{array}{rl@{\qquad}rl} \dfrac{\sin A}{a}&=\dfrac{\sin C_{1}}{c_{1}} & \dfrac{\sin A}{a}&=\dfrac{\sin C_{2}}{c_{2}} \\ \dfrac{\sin 35{{}^\circ}}{6}&=\dfrac{\sin 95.1{{}^\circ}}{c_{1}} & \dfrac{\sin 35{{}^\circ}}{6}&=\dfrac{\sin 14.9{{}^\circ}}{c_{2}} \\ c_{1}&=\dfrac{6\sin 95.1{{}^\circ}}{\sin 35{{}^\circ}}\approx 10.42 & c_{2}&=\dfrac{6\sin 14.9{{}^\circ}}{\sin 35{{}^\circ}}\approx 2.69 \end{array} \] The two solved triangles are illustrated in Figure 63.
Cases 3 and 4 are solved using the Law of Cosines.
THEOREM Law of Cosines
For a triangle with sides \(a\,\), \(b\), \(c\) and opposite angles \(A\), \(B\) , \(C\), respectively, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{@{}l@{}} {\color{#0066A7}•}\enspace c^{2} = a^{2}+b^{2}-2ab\cos C\\[3pt] {\color{#0066A7}•}\enspace b^{2} = a^{2}+c^{2}-2ac\cos B\\[3pt] {\color{#0066A7}•}\enspace a^{2} = b^{2}+c^{2}-2bc\cos A \end{array} }}\]
NOTE
If the triangle is a right triangle, the Law of Cosines reduces to the Pythagorean Theorem.
Using the Law of Cosines to Solve a Triangle
Solve the triangle: \(a=2\), \(b=3\), \(\ C=60^\circ\) shown in Figure 64.
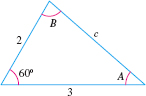
Solution Because two sides \(a\) and \(b\) and the included angle \(C=60^\circ\) (SAS) are known, we use the Law of Cosines to find the third side \(c\). \begin{eqnarray*} c^{2} &=&a^{2}+b^{2}-2ab\cos C=2^{2}+3^{2}-2\cdot 2\cdot 3\cdot \cos 60 {{}^\circ}=13-\left( 12\cdot \dfrac{1}{2}\right) =7 \\ c &=&\displaystyle\sqrt{7} \end{eqnarray*}
Side \(c\) is of length \(\displaystyle\sqrt{7}\). To find either the angle \(A\) or \(B\), use the Law of Cosines. For \(A\), \begin{eqnarray*} a^{2} &=&b^{2}+c^{2}-2bc\cos A \\[3pt] 2bc\cos A &=&b^{2}+c^{2}-a^{2} \\[6pt] \cos A &=&\dfrac{b^{2}+c^{2}-a^{2}}{2bc}=\dfrac{9+7-4}{2\cdot 3\displaystyle\sqrt{7}}=\dfrac{12}{6\displaystyle\sqrt{7}}=\dfrac{2\displaystyle\sqrt{7}}{7} \\[6pt] A &\approx& 40.9^\circ \end{eqnarray*}
Then to find the third angle, use the fact that the sum of the angles of a triangle, when measured in degrees, equals \(180 {{}^\circ}.\) That is, \begin{eqnarray*} 40.9^\circ+B+60^\circ&=&180^\circ\nonumber \\[0pt] B &=&79.1^\circ \end{eqnarray*}