10.6 Assess Your UnderstandingPrinted Page 741
741
Concepts and Vocabulary
True or False The symmetric equations \(\dfrac{x-3}{2}= \dfrac{y-4}{1}=\dfrac{z+2}{-1}\) represent a line parallel to the vector \(3 \mathbf{i}+4\mathbf{j}-2\mathbf{k}\).
False
True or False Skew lines can sometimes lie in the same plane.
False
True or False If two planes are not parallel, they intersect in a line.
True
True or False The two planes \(p_{1}\): \(2x+3y-z=3\) and \(p_{2}\): \(6x+3y-3z=9\) are parallel.
False
True or False The planes \(x+2y+z=3\) and \(x+2y+z=4\) are parallel and are 1 unit apart.
False
Which of the three representations of a line in space do you like best? Give reasons for your choice.
Answers will vary.
Which of the two representations of a plane in space do you like better? Give reasons for your choice.
Answers will vary.
Two distinct lines in space that do not intersect and are not parallel are called ___________.
Skew
Skill Building
In Problems 9–12, find:
- (a) A vector equation
- (b) Parametric equations
- (c) Symmetric equations of the line
containing the point \((1,2,3)\) and in the direction of \(2\mathbf{i}-\mathbf{j}+\mathbf{k}\).
- (a) \(\mathbf{r}(t)=(1+2t)\mathbf{i}+(2-t)\mathbf{j}+(3+t)\mathbf{k}\)
- (b) \(x=1+2t\), \(y=2-t\), \(z=3+t\)
- (c) \(\dfrac{x-1}2=\dfrac{y-2}{-1}=\dfrac{z-3}{1}\)
containing the point \((4,-1,6)\) and in the direction of \(\mathbf{i}+\mathbf{j}\).
containing the points \(P_{0}=(1,-1,3)\) and \(P_{1}=(4,2,1)\).
- (a) \(\mathbf{r}(t)=(1+3t)\mathbf{i}+(-1+3t)\mathbf{j}+(3-2t)\mathbf{k}\)
- (b) \(x=1+3t\); \(y=-1+3t\); \(z=3-2t\)
- (c) \(\dfrac{x-1}{3}=\dfrac{y+1}{3}=\dfrac{z-3}{-2}\)
containing the points \(P_{0}=(-2,3,0)\) and \(P_{1}=(1,-1,2)\).
Find parametric equations of a line containing the point \( (-1,5,6)\) and in the direction of the line \(\dfrac{x+1}{5}=\dfrac{y-2}{4}= \dfrac{z-3}{-3}.\)
\(x=-1+5t\), \(y=5+4t\), \(z=6-3t\)
Find parametric equations of a line containing the point \( (1,-2,-3)\) and in the direction of the line \(\dfrac{x+1}{6}=\dfrac{y+2}{2}=\dfrac{z}{-1}.\)
Let \(\dfrac{x-4}{2}=\dfrac{y+1}{-1}=\dfrac{z-2}{2} \) be symmetric equations of a line. Find a vector in the direction of the line, and find two points on this line.
Answers will vary.
Let \(x+1=y+3=\dfrac{z+4}{2}\) be symmetric equations of a line. Find a vector in the direction of the line, and find two points on this line.
In Problems 17–22, find symmetric equations of the line containing the point \(P_{0}\).
\(P_{0}=(4,2,1)\) and the line is in the direction of the vector \(\mathbf{D=}\) \(2\mathbf{i}+\mathbf{k}\).
\(y=2\), \(\dfrac{x-4}2=\dfrac{z-1}1\)
\(P_{0}=(-1,2,0)\) and the line is in the direction of the vector \(\mathbf{D=}\) \(2\mathbf{k-j}\).
\(P_{0}=(0,0,0)\) and the line is perpendicular to each of the lines \(\dfrac{x+1}{2}=\dfrac{y-1}{3}=\dfrac{z}{-2}\) and \(\dfrac{x-3}{3}= \dfrac{y}{1}=\dfrac{z+1}{2}\).
\(\dfrac{x}8=\dfrac{y}{-10}=\dfrac{z}{-7}\) or \(\dfrac{x}{-8}=\dfrac{y}{10}=\dfrac{z}{7}\)
\(P_{0}=(0,0,0)\) and the line is perpendicular to each of the lines \(\dfrac{x+2}{4}=\dfrac{y-1}{2}=z+1\) and \(\dfrac{x+5}{5}=\dfrac{y+1}{3} =z\).
\(P_{0}=(1,2,-1)\) and the line is perpendicular to the vectors \(\mathbf{u}=2\mathbf{i}+4\mathbf{j}-2\mathbf{k}\) and \(\ \mathbf{v}=-3 \mathbf{i}-2\mathbf{j}+\mathbf{k}\).
\(x=1, \dfrac{y-2}4=\dfrac{z+1}8\)
\(P_{0}=(-1,3,2)\) and the line is perpendicular to the vectors \(\mathbf{u}=-2\mathbf{i}+2\mathbf{j}-3\mathbf{k}\) and \(\mathbf{v}=4\mathbf{ i}+2\mathbf{j}+\mathbf{k}\).
In Problems 23–30:
- (a) Determine whether the lines \(l_{1}\) and \(l_{2}\) intersect, are parallel, or are skew.
- (b)
 Graph the lines. Does the graph confirm the answer to (a)?
Graph the lines. Does the graph confirm the answer to (a)?
\(\begin{array}[t]{ll} l_{1}\hbox{:} & \mathbf{r}_{1}=2\mathbf{i}-2\mathbf{k}+t_{1}\left( -3\, \mathbf{i}+6\,\mathbf{j}+6\,\mathbf{k}\right) \\ l_{2}\hbox{:} & \mathbf{r}_{2}=6\,\mathbf{i}+2\,\mathbf{j}+5\,\mathbf{k} +t_{2}\,\left( -\mathbf{i}+2\,\mathbf{j}+2\,\mathbf{k}\right) \end{array}\)
(a, b) Parallel
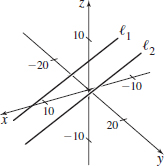
\(\begin{array}[t]{ll} l_{1}\hbox{:} & \mathbf{r}_{1}=3\,\mathbf{i}+3\,\mathbf{k}+t_{1}\left( 3 \mathbf{i}+6\,\mathbf{j}-2\,\mathbf{k}\right) \\ l_{2}\hbox{:} & \mathbf{r}_{2}=3\,\mathbf{i}+3\,\mathbf{k}+t_{2}\left( -2\, \mathbf{i}+4\,\mathbf{j}+7\,\mathbf{k}\right) \end{array}\)
\(\begin{array}[t]{ll} l_{1}\hbox{:} & \mathbf{r}_{1}=4\mathbf{i}+3\,\mathbf{j}+t_{1}\left( \mathbf{i}-\mathbf{j}+6\mathbf{k}\right) \\ l_{2}\hbox{:} & \mathbf{r}_{2}=4\,\mathbf{i}+3\,\mathbf{j}+2\,\mathbf{k} +t_{2}\left( \mathbf{i}-\mathbf{j}-2\,\mathbf{k}\right) \end{array}\)
(a, b) Intersect when \(t=\dfrac14\) at the point \((17/4,11/4,3/2)\)
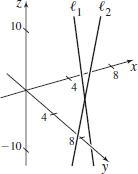
\(\begin{array}[t]{ll} l_{1}\hbox{:} & \mathbf{r}_{1}=2\mathbf{i}+7\,\mathbf{j}+t_{1}\left( -2\, \mathbf{i}+8\,\mathbf{j}-6\,\mathbf{k}\right) \\ l_{2}\hbox{:} & \mathbf{r}_{2}=6\,\mathbf{i}-5\,\mathbf{j}+t_{2}\,\left( \mathbf{i}-4\,\mathbf{j}+3\mathbf{k}\right) \end{array}\)
\(\begin{array}[t]{ll} l_{1}\hbox{:} & \dfrac{x-3}{2}=\dfrac{y+2}{3}=\dfrac{z-1}{4} \\ l_{2}\hbox{:} & \dfrac{x+4}{-4}=\dfrac{y-3}{-6}=\dfrac{z+4}{-8} \end{array}\)
(a, b) Parallel

\(\begin{array}[t]{ll} l_{1}\hbox{:} & \dfrac{x}{3}=\dfrac{y-2}{4}=\dfrac{z+4}{1} \\ l_{2}\hbox{:} & \dfrac{x+6}{3}=\dfrac{y+2}{4}=\dfrac{z-3}{2} \end{array}\)
\(\begin{array}[t]{ll} l_{1}\hbox{:} & \dfrac{x+1}{5}=\dfrac{y-2}{4}=\dfrac{z-3}{-3} \\ l_{2}\hbox{:} & \dfrac{x+1}{6}=\dfrac{y-2}{3}=\dfrac{z+3}{2} \end{array}\)
(a, b) Skew

\(\begin{array}[t]{ll} l_{1}\hbox{:} & \dfrac{x+5}{6}=\dfrac{y-2}{3}=\dfrac{z-4}{-1} \\ l_{2}\hbox{:} & {x}=\dfrac{y-2}{3}=\dfrac{z-8}{2} \end{array}\)
In Problems 31–40, find the general equation of each plane.
Containing the point \((1,-1,2)\) and normal to the vector \(2\mathbf{i}-\mathbf{j}+\mathbf{k}\)
\(2x-y+z=5\)
Containing the point \((-3,2,1)\) and normal to the vector \( \mathbf{i}+\mathbf{j}-2\mathbf{k}\)
Containing the point \((0,5,-2)\) and parallel to the plane \( x+2y-z=6\)
\(x+2y-z=12\)
Containing the point \((1,-2,0)\) and parallel to the plane \( 2x-y+3z=10\)
Containing the point \((2,3,-1)\) and normal to the line \[ \dfrac{x-1}{2}=\dfrac{y-3}{5}=\dfrac{z+1}{-2} \]
\(2x+5y-2z=21\)
742
Containing the point \((-1,2,3)\) and normal to the line \[ \dfrac{x+5}{3}=\dfrac{y+2}{4}=\dfrac{z-4}{4} \]
Parallel to the \(xy\)-plane and containing the point \(\left( 0,0,4\right)\)
\(z=4\)
Parallel to the \(yz\)-plane and containing the point \(\left( 2,0,0\right)\)
Parallel to the \(xz\)-plane and containing the point \((1,-2,3)\)
\(y=-2\)
Parallel to the \(xy\)-plane and containing the point \((1,-3,4)\)
In Problems 41–46:
- (a) Find the general equation of the plane containing the points \(P_{1}\), \(P_{2}\), and \(P_{3}\).
- (b)
 Graph the plane.
Graph the plane.
\(P_{1}=(0,0,0)\); \(P_{2}=(1,2,-1)\); \(P_{3}=(-1,1,0)\)
- (a) \(x+y+3z=0\)
- (b)
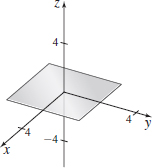
\(P_{1}=(0,0,0)\); \(P_{2}=(3,-1,2)\); \(P_{3}=(-3,1,0)\)
\(P_{1}=(1,2,1)\); \(P_{2}=(3,2,2)\); \(P_{3}=(4,-1,-1)\)
- (a) \(3x\,{+}\,7y\,{-}\,6z=11\)
- (b)
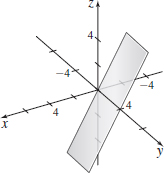
\(P_{1}=(-1,2,0)\); \(P_{2}=(3,4,-1)\); \(P_{3}=(-2,-1,0)\)
\(P_{1}=(6,8,-2)\); \(P_{2}=(4,-1,0)\); \(P_{3}=(1,0,0)\)
- (a) \(2x\,{+}\,6y\,{+}\,29z=2\)
- (b)
\(P_{1}=(-3,-4,0)\); \(P_{2}=(6,-7,2)\); \(P_{3}=(0,0,1)\)
In Problems 47–50, find symmetric equations of the line of intersection of the two planes.
\(p_{1}\): \(x+y-z=-5\) and \(p_{2}\): \(\ 2x+3y-4z=-1\)
\(\dfrac{x+14}{-1}=\dfrac{y-9}{2}=\dfrac{z}{1}\)
\(p_{1}\): \(\ 2x-y+z=2\) and \(p_{2}\): \(x+y+z=3\)
\(p_{1}\): \(x-y=2\) and \(p_{2}\): \(\ y-z=2\)
\(\dfrac{x-4}1=\dfrac{y-2}1=\dfrac{z}1\)
\(p_{1}\): \(\ 2x-3y+z=1\) and \(p_{2}\): \(\ 2x-3y+4z=2\)
In Problems 51–54, find the distance from the point to the plane.
from \((1, 2,-1)\) to \(2x-y+z=1\)
\(\dfrac{\sqrt{6}}{3}\)
from \((-1,3,-2)\) to \(x+2y-3z=4\)
from \(\left( 2,-1,\,1\right)\) to \(-x+y-3z=6\)
\(\dfrac{12\sqrt{11}}{11}\)
from \((-2,1,1)\) to \(-3x+2y+z=1\)
In Problems 55–58, find the distance between the two parallel planes.
\(p_{1}\): \(2x+y-2z=-1\) and \(p_{2}\): \(2x+y-2z=3\)
\(\dfrac43\)
\(p_{1}\): \(x+2y-2z=-3\) and \(p_{2}\): \(\ x+2y-2z=3\)
\(p_{1}\): \(x-2z=-1\) and \(p_{2}\): \(x-2z=3\)
\(\dfrac{4\sqrt{5}}{5}\)
\(p_{1}\): \(-x+y+2z=-4\) and \(p_{2}\): \(-x+y+2z=-1\)
In Problem 59-62, find the point of intersection of the plane and the line.
Plane \(2x+y-z=5\), line \(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-1 }{1}\)
\((3,1,2)\)
Plane \(x+y-2z=8\), line \(\dfrac{x+1}{2}=\dfrac{y-3}{1}=\dfrac{z-4 }{-2}\)
Plane \(2x+3y+z=5,\) line \(\dfrac{x-3}{1}=\dfrac{y+4}{2}=\dfrac{ z-1}{2}\)
\((4,-2,3)\)
Plane \(x+y-z=3;\) line \(\dfrac{x+2}{2}=\dfrac{y-3}{1}=\dfrac{z}{2 }\)
Applications and Extensions
In Problems 63–66, find the point of intersection of \(l_{1}\) and \(l_{2}\) and the angle between them.
\(\begin{array}[t]{ll} l_{1}\hbox{:} & \mathbf{r}_{1}=(2-t_{1})\mathbf{i}+(4+2t_{1})\mathbf{j} +(-5+t_{1})\mathbf{k} \\ l_{2}\hbox{:} & \mathbf{r}_{2}=(4-t_{2})\mathbf{i}+(3+t_{2})\mathbf{j} +(-13+3t_{2})\mathbf{k} \end{array}\)
\((1,6,-4)\); \(\theta=\sin^{-1}\left(\sqrt{\dfrac{5}{11}}\right)\) \(\approx 0.740\) radians
\(\begin{array}[t]{ll} l_{1}\hbox{:} & \mathbf{r}_{1}=(5+2t_{1})\mathbf{i}+(6-t_{1})\mathbf{j} +2t_{1}\mathbf{k} \\ l_{2}\hbox{:} & \mathbf{r}_{2}=(7+3t_{2})\mathbf{i}+(5-2t_{2})\mathbf{j} +(2-t_{2})\mathbf{k} \end{array}\)
\(\begin{array}[t]{ll} l_{1}\hbox{:} & \mathbf{r}_{1}=t_{1}\mathbf{i}+(1+2t_{1})\mathbf{j} +(-3+t_{1})\mathbf{k} \\ l_{2}\hbox{:} & \mathbf{r}_{2}=(-3+t_{2})\mathbf{i}+(1-4t_{2})\mathbf{j} +(2-7t_{2})\mathbf{k} \end{array}\)
\((-2,-3,-5)\); \(\theta=\sin^{-1}\left(\dfrac{10}{\sqrt{198}}\right)\approx 0.790\) radians
\(\begin{array}[t]{ll} l_{1}\hbox{:} & \mathbf{r}_{1}=(2-3t_{1})\mathbf{i}+6t_{1}\mathbf{j} +(-2+5t_{1})\mathbf{k} \\ l_{2}\hbox{:} & \mathbf{r}_{2}=-2t_{2}\mathbf{i}+(1+t_{2})\mathbf{j}+2t_{2} \mathbf{k} \end{array}\)
- (a) Find parametric equations of the line containing the point \((1,2,-1)\) and normal to the plane \(2x-y+z-6=0.\)
- (b)
 Graph the line and the plane.
Graph the line and the plane.
- (a) x (t) = 1 + 2t, y (t) = 2 − t, z (t) = −1 + t
- (b)
- (a) Find parametric equations of the line containing the point \((2,3,-1)\) and normal to the plane \(x+y-z-3=0\).
- (b)
 Graph the line and the plane.
Graph the line and the plane.
What property can you assign to the lines \(l_{1}\) and \(l_{2}\) , given below, if \(a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}=0\)? \[ \begin{array}{ll} l_{1}\hbox{:} & \dfrac{x-x_{1}}{a_{1}}=\dfrac{y-y_{1}}{a_{2}}=\dfrac{ z-z_{1}}{a_{3}} \\ l_{2}\hbox{:} & \dfrac{x-x_{1}}{b_{1}}=\dfrac{y-y_{1}}{b_{2}}=\dfrac{ z-z_{1}}{b_{3}} \end{array} \]
\(\ell_1\) and \(\ell_2\) are perpendicular.
What property can you assign to the distinct lines \(l_{1}\) and \( l_{2}\), given below, if \(\dfrac{a_{1}}{b_{1}}=\dfrac{a_{2}}{b_{2}}=\dfrac{ a_{3}}{b_{3}}?\) \[ \begin{array}{ll} l_{1}\hbox{:} & \dfrac{x-x_{1}}{a_{1}}=\dfrac{y-y_{1}}{a_{2}}=\dfrac{z-z_{1} }{a_{3}} \\ l_{2}\hbox{:} & \dfrac{x-x_{2}}{b_{1}}=\dfrac{y-y_{2}}{b_{2}}=\dfrac{ z-z_{2}}{b_{3}} \end{array} \]
Problems 71–76 use the following discussion. When two planes intersect, the angle \(\theta\) between the planes is defined as the non-obtuse angle between their normals. See the figure. If \( \mathbf{N}_{1}\) and \(\mathbf{N}_{2}\) are the normals of two intersecting planes, the angle \(\theta\) between these planes is given by \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox \cos \theta =\dfrac{\left\vert \mathbf{N}_{1}\,{\cdot}\, \mathbf{N}_{2}\right\vert }{\Vert \mathbf{N}_{1}\Vert \Vert \mathbf{N}_{2}\Vert }\qquad 0\leq \theta \leq \dfrac{\pi }{2}} \]
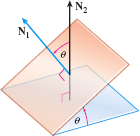
In Problems 71–76, the two planes intersect. Find the angle between them.
\(p_{1}\): \(\ 2x-y+z=2\) and \(p_{2}\): \(x+y+z=3\)
\(\cos^{-1}\left(\dfrac{\sqrt{18}}9\right)\approx 1.080\) radians
\(p_{1}\): \(\ x+y-z=5\); and \(p_{2}\): \(\ 2x+3y-4z=1\)
\(p_{1}\): \(\ 2x-3y+z=1\) and \(p_{2}\): \(\ 2x-3y+4z=2\)
\(\cos^{-1}\left(\dfrac{17}{\sqrt{406}}\right)\approx 0.567\) radians
743
\(p_{1}\): \(x-y=2\) and \(p_{2}\): \(\ y-z=2\)
\(p_{1}\): \(\ 2x-y+z=3\) and \(p_{2}\): \(\ 4x-y+6z=7\)
\(\cos^{-1}\left(\dfrac{5\sqrt{318}}{106}\right)\approx 0.571\) radians
\(p_{1}\): \(\ x+y-z=1\) and \(\ p_{2}\): \(\ 2x-2y+2z=-2\)
Paths of Spacecrafts Two unidentified flying objects are at the points \((t,-t, 1-t)\) and \((t-3, 2t, 4t-1)\) at time \(t\), \(t\geq 0.\)
- (a) Describe the paths of the objects.
- (b) Find the acute angle between the paths.
- (c) Find where the paths intersect (or determine that they do not).
- (d) Will the objects collide?
- (a) Each path is a straight line.
- (b) 0.889
- (c) The paths do intersect.
- (d) No. Answers will vary.
Find symmetric equations of the line passing through the centers of the spheres \[ x^{2}+y^{2}+z^{2}-2x-4y+4z=8 \]
and \[ x^{2}+y^{2}+z^{2}+2x+6y+4z=20 \]
Find parametric equation of the line perpendicular to the lines \[ l_{1}\hbox{:}\quad x=1-t,\quad y=t,\quad z=2t-1 \]
and \[ l_{2}:\quad x=t+1,\quad y=-t,\quad z=t-1 \]
at their point of intersection. Why is this line parallel to the \(xy\)-plane?
\(x=1+3t\), \(y=3t\), \(z=-1\); Answers will vary.
Explain why the set of points \((x,y,z)\) equidistant from the points \((1,3,0)\) and \((-1,1,2)\) is a plane. Then find its equation in two ways, as follows:
- (a) Use the distance formula to equate the distances between \( (x,y,z)\) and the given points, simplifying the result to obtain an equation of the plane.
- (b) Find a point on the plane and a vector normal to the plane, and use the answer to find an equation of the plane.
Find symmetric equations of the line of intersection of the planes \(2x+y-z=6\) and \(x-y+3z=4\).
\(\dfrac{x-\dfrac{10}{3}}{2}=\dfrac{y+\dfrac{2}{3}}{-7}=\dfrac{z}{-3}\)
Find symmetric equations of the line that contains \((2,0,-3)\) , is perpendicular to \(\mathbf{i}+2\mathbf{j}-\mathbf{k}\), and is parallel to the plane \(2x+3y-z=1\).
Find the point of intersection of the line through the points \((0,2,-2)\), and \((2,1,-3)\), and the plane through the points \((0,4,-2)\), \((1,3,-2)\), and \( (2,2,-3)\).
\((4,0,-4)\)
Find an equation of the plane parallel to the line \(\mathbf{r} =2\mathbf{i}+t(-\mathbf{i}+\mathbf{j}+2\mathbf{k})\) and containing the points \((2,2,-1)\) and \((1,0,1)\).
Find an equation of the plane tangent to the sphere \( (x-1)^{2}+(y+2)^{2}+(z-2)^{2}=6\) at the point \((2,-1, 0)\).
\(x+y-2z=1\)
Sphere Find an equation of the sphere with its center at \((-2,1,5)\) and tangent to \(x+2y-2z=8\).
Find symmetric equations of a line normal to the plane containing the lines \[ x-2=\frac{y+1}{2}=\frac{z-1}{2}\qquad \hbox{and }\qquad x+1=\frac{y+8}{3}= \frac{z}{-3} \]
at their point of intersection.
\(\dfrac{x}{-12}=\dfrac{y+5}5=\dfrac{z+3}1\)
Challenge Problems
Find an equation for the plane containing the origin that is perpendicular to the plane \(x-2y-z=0\) and makes an angle of \(60^{\circ}\) with the positive \(y\)-axis.
We proved that the distance between the point \( P_{0}=(x_{0}, y_{0}, z_{0})\) and the plane \(Ax+By+Cz=D\) is \[ d=\frac{|Ax_{0}+By_{0}+Cz_{0}-D|}{\sqrt{A^{2}+B^{2}+C^{2}}} \]
Derive this formula differently, as follows:
- (a) Show that the line through \(P_{0}\) normal to the plane has the parametric equations \(x=x_{0}+At\), \(y=y_{0}+Bt\), \(z=z_{0}+Ct\).
- (b) If \(P=(x, y, z)\) is the point of intersection of the line in (a) with the plane, show that \(x-x_{0}=At\), \(y-y_{0}=Bt\), \(z-z_{0}=Ct\), where \[ t=\frac{-(Ax_{0}+By_{0}+Cz_{0})+D}{A^{2}+B^{2}+C^{2}} \]
- (c) Explain why \(d\) is the distance between \(P_{0}\) and \(P\), and use the distance formula to finish the proof.
- (a) See Student Solutions Manual.
- (b) See Student Solutions Manual.
- (c) Answers will vary.
Prove that the distance between the parallel planes \( Ax+By+Cz=D_{1}\) and \(Ax+By+Cz=D_{2}\) is \[ d=\frac{|D_{2}-D_{1}|}{\sqrt{A^{2}+B^{2}+C^{2}}} \]
Let two skew lines have respective direction vectors \(\mathbf{ D}_{1}\) and \(\mathbf{D}_{2}\). Let \(A\) and \(B\) be points on the respective lines, and let \(\mathbf{w}=\skew5\overrightarrow{\it AB}\). Show that the distance between the two lines is the magnitude of the vector projection of \(\mathbf{w }\) onto \(\mathbf{D}_{1}\times \mathbf{D}_{2}\): \[ |\hbox{proj}_{\mathbf{D}_{1}\times \mathbf{D}_{2}}\mathbf{w}|=\frac{|\mathbf{ w}\,{\cdot}\, (\mathbf{D}_{1}\times \mathbf{D}_{2})|}{\Vert \mathbf{D}_{1}\times \mathbf{D}_{2}\Vert } \]
(The shortest distance is measured along the common perpendicular to the two lines.)
See Student Solutions Manual.
Find the distance between the lines \(\dfrac{x-3}{2}=\dfrac{y }{3}=z\qquad\) and \(\qquad x=\dfrac{y+1}{-2}=\dfrac{z-2}{-1}\).
What is the minimum distance between the skew lines \( x-1=y-2=z+6\) and \(\dfrac{x-1}{2}=\dfrac{y+2}{-3}=z-10\)? Locate the points on each line at which the distance is minimum.

