10.7 Quadric Surfaces
744
OBJECTIVES
When you finish this section, you should be able to:
- Identify quadric surfaces based on an ellipse (p. 744)
- Identify quadric surfaces based on a hyperbola (p. 746)
- Identify cylinders (p. 748)
- Graph quadric surfaces (p. 750)
The graph of a second degree equation in two variables \[ \begin{equation*} Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0 \end{equation*}\]
is a conic (a parabola, an ellipse or a hyperbola), except for degenerate cases.
NEED TO REVIEW?
Conics are discussed in Appendix A.3, pp. A-22 to A-25.
The graph of a second-degree equation in three variables \[\bbox[5px, border:1px solid black, #F9F7ED]{ Ax^{2}+By^{2}+Cz^{2}+Dxy+Exz+Fyz+Gx+Hy+Iz+J=0 }\tag{1} \]
is called a quadric surface. There are nine different types of quadric surfaces, excluding the degenerate cases. Examples of degenerate quadric surfaces include \(x^{2}+y^{2}+z^{2}=0\), whose graph is the point \((0,0,0),\) and \(2x^{2}+3y^{2}+4z^{2}=-2\), whose graph has no points.
As with conics, when the equation of a quadric surface is written in the form of equation (1), it is in general form. On the other hand, if we complete the squares, it is in standard form. The equations we consider here are in standard form and the corresponding quadric surfaces are centered at the origin of an \(xyz\)-coordinate system. Variations of these surfaces can be found using transformations (discussed in Chapter P, Section 3.)
A quadric surface is characterized by listing its intercepts, and by finding its traces. A trace is the intersection of the surface with a coordinate plane or a plane parallel to a coordinate plane. The term section (or cross section) is sometimes used when the intersection is with a plane other than a coordinate plane.
1 Identify Quadric Surfaces Based on an Ellipse
The first three quadric surfaces we investigate are based on an ellipse. Each of these surfaces has at least one trace that is an ellipse.
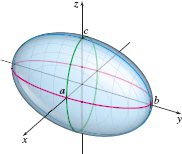
spanDEFINITIONspan Ellipsoid
The graph of an ellipsoid has an equation of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}=1\qquad a\gt0,\, b\gt0,\, c\gt0 } \]
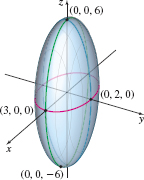
See Figure 58. The intercepts of an ellipsoid are the points \((\pm a,0,0)\), \((0,\pm b,0)\), and \((0,0,\pm c)\), and every trace is an ellipse. For example, if \(z=0,\) the trace in the \(xy\) -plane is the ellipse \(\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1\). The traces parallel to the \(xy\)-plane are the ellipses \(\dfrac{x^{2}}{a^{2}}+ \dfrac{y^{2}}{b^{2}}=1-\dfrac{k^{2}}{c^{2}},\) where \(\left\vert z \right\vert =\left\vert k\right\vert \lt c\). Traces parallel to the \(xz\)- and \(yz\)-planes are the ellipses \(\dfrac{x^{2}}{a^{2}}+\dfrac{z^{2}}{c^{2}}=1-\dfrac{k^{2}}{b^{2}},\) where \(\left\vert y \right\vert =\vert k\vert \lt b,\) and \(\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2} }{c^{2}}=1-\dfrac{k^{2}}{a^{2}},\) where \(\left\vert x \right\vert =\vert k\vert \lt a, \) respectively.
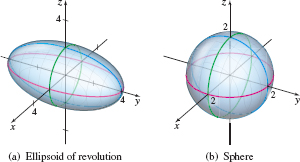
An ellipsoid centered at the origin is symmetric with respect to each coordinate plane. The symmetry holds because all three variables are squared. If two of the three numbers \(a\), \(b\), or \(c\) are equal, the ellipsoid is called an ellipsoid of revolution. If all three numbers \(a\), \(b\), and \(c\) are equal, the ellipsoid is a sphere. See Figure 59.
745
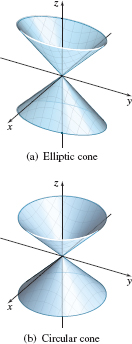
The second quadric surface based on an ellipse is called an elliptic cone.
spanDEFINITIONspan Elliptic Cone
The graph of an elliptic cone has an equation of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{ z^{2}=\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}\qquad a\gt0, b\gt0 } \]
See Figure 60(a). The only intercept of an elliptic cone is the origin \( (0,0,0)\), called the vertex of the cone. The trace of an elliptic cone in the \(xy\)-plane is the origin. Traces parallel to the \(xy\)-plane are ellipses centered on the \(z\)-axis. The trace in the \(yz\)-plane consists of the pair of intersecting lines \(z=\pm \dfrac{y}{b}\), and the trace in the \( xz\)-plane consists of the pair of intersecting lines \(z=\pm \dfrac{x}{a}\).
If \(a=b\), the elliptic cone becomes a circular cone and its traces are circles. See Figure 60(b). Other forms of an elliptic cone are \[\bbox[5px, border:1px solid black, #F9F7ED]{ x^{2}=\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}\qquad y^{2}=\dfrac{x^{2}}{a^{2}}+\dfrac{z^{2}}{c^{2}}\qquad a\gt0, b\gt0, c\gt0 } \]
The third quadric surface based on the ellipse is the elliptic paraboloid.
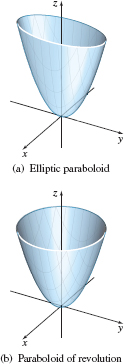
spanDEFINITIONspan Elliptic Paraboloid
The graph of an elliptic paraboloid has an equation of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{ z=\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}} \qquad a\gt0, b\gt0 } \]
See Figure 61(a). An elliptic paraboloid has only one intercept, the origin \( (0,0,0)\), called the vertex. The trace of an elliptic paraboloid in the \(xy\)-plane is the vertex. The traces parallel to the \(xy\)-plane are ellipses. The traces in the other two coordinate planes are parabolas: \(z= \dfrac{y^{2}}{b^{2}}\) in the \(yz\)-plane, and \(z=\dfrac{x^{2}}{a^{2}}\) in the \(xz\)-plane. Traces parallel to the \(xz\)- and \(yz\)-coordinate planes are parabolas. Since \(z\ge0\), the surface (except for the origin) lies above the \(xy\)-plane.
If \(a=b\), the surface is a paraboloid of revolution, and the traces parallel to the \(xy\)-plane are circles. See Figure 61(b).
746
Other forms of an elliptic paraboloid are \[\bbox[5px, border:1px solid black, #F9F7ED]{ x=\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}\qquad y= \dfrac{x^{2}}{a^{2}}+\dfrac{z^{2}}{c^{2}}\qquad a\gt0, b\gt0, c\gt0 } \]

Identifying Quadric Surfaces
Identify each quadric surface. List its intercepts and its traces in the coordinate planes.
- \(4x^{2}+9y^{2}+z^{2}=36\)
- \(x=\dfrac{y^{2}}{4}+z^{2}\)
Solution (a) We recognize this as an ellipsoid because it has three squared terms and all the coefficients are positive. To find its intercepts and traces, divide the equation by \(36\) to put it in standard form. \[ \begin{eqnarray*} \dfrac{x^{2}}{9}+\dfrac{y^{2}}{4}+\dfrac{z^{2}}{36} &=&1 \\ \dfrac{x^{2}}{3^{2}}+\dfrac{y^{2}}{2^{2}}+\dfrac{z^{2}}{6^{2}} &=&1 \end{eqnarray*} \]
The intercepts of the ellipsoid are \((3,0,0)\), \((-3,0,0)\), \((0,2,0)\), \( (0,-2,0)\), \((0,0,6)\), and \((0,0,-6)\).
The traces are all ellipses. In the \(xy\)-plane, the trace is \(\dfrac{x^{2}}{9} +\dfrac{y^{2}}{4}=1;\) in the \(xz\)-plane, the trace is \(\dfrac{x^{2}}{9}+ \dfrac{z^{2}}{36}=1;\) and in the \(yz\)-plane, the trace is \(\dfrac{y^{2}}{4}+ \dfrac{z^{2}}{36}=1.\) Figure 62 shows the graph of the ellipsoid.
(b) This equation defines an elliptic paraboloid. Its only intercept (vertex) is \((0,0,0)\).
The trace in the \(yz\)-plane is the vertex \((0,0,0)\) and traces parallel to the \(yz\)-plane are ellipses, provided \(x\gt0\).
To find the trace in the \(xy\)-plane, let \(z=0\). The trace is the parabola \(x= \dfrac{y^{2}}{4}.\) To find the trace in the \(xz\)-plane, let \(y=0\). The trace is the parabola \( x=z^{2}\).

Figure 63 shows the graph of the elliptic paraboloid.
NOW WORK
Problems 9(a) and 9(b).
2 Identify Quadric Surfaces Based on a Hyperbola
There are three quadric surfaces that are based on a hyperbola. Each of these surfaces has at least one trace that is a hyperbola.
spanDEFINITIONspan Hyperbolic Paraboloid
The graph of a hyperbolic paraboloid has an equation of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{ z=\dfrac{y^{2}}{b^{2}}-\dfrac{x^{2}}{a^{2}}\qquad a\gt0, b\gt0 } \]
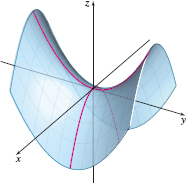
See Figure 64. The origin is the only intercept of the hyperbolic paraboloid. The trace in the \(xy\)-plane is the pair of lines \(\dfrac{y}{b} =\pm \dfrac{x}{a},\) which intersect at the origin. The traces parallel to the \(xy\)-plane are hyperbolas given by the equations \(\dfrac{y^{2}}{b^{2}}- \dfrac{x^{2}}{a^{2}}=k,\) where \(z=k.\)
747
The trace in the \(xz\)-plane is the parabola \(z=-\dfrac{x^{2}}{a^{2}}\), which opens down. Traces parallel to the \(xz\)-plane are also parabolas that open down. The trace in the \(yz\)-plane is the parabola \(z=\dfrac{y^{2}}{b^{2}},\) which opens up. Traces parallel to the \(yz\)-plane are also parabolas that open up.
Notice that the origin is a minimum point for the trace in the \(yz\)-plane and is a maximum point for the trace in the \(xz\)-plane. Because of the graph’s appearance, the origin is called a saddle point of the surface.
Other forms of a hyperbolic paraboloid are \[\bbox[5px, border:1px solid black, #F9F7ED]{ x=\dfrac{y^{2}}{b^{2}}-\dfrac{z^{2}}{c^{2}}\qquad y= \dfrac{x^{2}}{a^{2}}-\dfrac{z^{2}}{c^{2}}\qquad a\gt0, b\gt0, c\gt0 } \]
spanDEFINITIONspan Hyperboloid of One Sheet
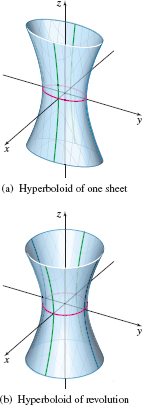
The graph of a hyperboloid of one sheet has an equation of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}-\dfrac{z^{2}}{c^{2}}=1\qquad a\gt0, b\gt0, c\gt0 } \]
See Figure 65(a). The intercepts a hyperboloid of one sheet are \((\pm \,a,0,0)\) and \((0,\pm b,0)\). The trace in the \(xy\)-plane is the ellipse \( \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1\), and all traces parallel to the \(xy\)-plane are also ellipses. The trace in the \(yz\)-plane is the hyperbola \( \dfrac{y^{2}}{b^{2}}-\dfrac{z^{2}}{c^{2}}=1\); the trace in the \(xz\)-plane is the hyperbola \(\dfrac{x^{2}}{a^{2}}-\dfrac{z^{2}}{c^{2}}=1\). Traces parallel to the \(yz\)- and \(xz\)-planes are also hyperbolas. The \(z\)-axis is called the axis of the hyperboloid of one sheet.
If \(a=b\), the surface is a hyperboloid of revolution. See Figure 65(b). Other forms of a hyperboloid of one sheet are \[\bbox[5px, border:1px solid black, #F9F7ED]{ -\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{ z^{2}}{c^{2}}=1\qquad \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2} }{c^{2}}=1\qquad a\gt0, b\gt0, c\gt0 } \]
The equation defining a hyperboloid of one sheet has a 1 on the right side; the equation defining a hyperboloid of two sheets has a \(-1\) on the right.
spanDEFINITIONspan Hyperboloid of Two Sheets
The graph of a hyperboloid of two sheets has an equation of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}-\dfrac{z^{2}}{c^{2}}=-1\qquad a\gt0, b\gt0, c\gt0 } \]
NOTE
Remember the cooling towers from Chapter 6? They are physical examples of a hyperboloid of revolution.
A hyperboloid of two sheets is shown in Figure 66. It has two intercepts \( (0,0,c)\) and \(( 0,0,-c).\) Also, the surface consists of two parts, one for which \(z\geq c\), and the other for which \(z\le-c\).
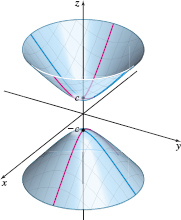
If \(z=0\), the equation has no real solution, so there is no trace in the \(xy\) -plane. Traces parallel to the \(xy\)-plane are ellipses and are defined for \( \vert z\vert \gt c\). The traces in the \(yz\)-plane and the \(xz\)-plane are the hyperbolas \(\dfrac{z^{2}}{c^{2}}-\dfrac{y^{2}}{b^{2}}=1\) and \(\dfrac{ z^{2}}{c^{2}}-\dfrac{x^{2}}{a^{2}}=1,\) respectively. Traces parallel to these coordinate planes are also hyperbolas. The \(z\)-axis is called the axis of the hyperboloid of two sheets.
748
Other forms of a hyperboloid of two sheets are \[\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}+\dfrac{ z^{2}}{c^{2}}=-1\qquad -\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{ z^{2}}{c^{2}}=-1\qquad a\gt0, b\gt0, c\gt0 } \]

Identifying Quadric Surfaces
Identify each quadric surface. List its intercepts and its traces in the coordinate planes.
- \(x^{2}-y^{2}+z^{2}=-9\)
- \(z=\dfrac{x^{2}}{9}-\dfrac{y^{2}}{4}\)
Solution (a) We begin by dividing the equation by \(9\) to put it in standard form. \[ \dfrac{x^{2}}{9}-\dfrac{y^{2}}{9}+\dfrac{z^{2}}{9}=-1 \]
This is a hyperboloid of two sheets. It has two intercepts \(( 0,3,0)\) and \((0,-3,0).\) If \(y=0\), the equation has no real solution, so there is no trace in the \(xz\)-plane. Traces parallel to the \(xz\)-plane are ellipses and are defined for \(\left\vert y\right\vert \gt3.\) The trace in the \(xy\)-plane is the hyperbola \(\dfrac{y^{2}}{9}-\dfrac{x^{2}}{ 9}=1\) and the trace in the \(yz\)-plane is the hyperbola \(\dfrac{y^{2}}{9}- \dfrac{z^{2}}{9}=1.\) Traces parallel to the \(xy\)- and \(yz\)-plane are also hyperbolas.
The \(y\)-axis is the axis of this hyperboloid of two sheets. See Figure 67 for the graph.
(b) This equation defines a hyperbolic paraboloid. The only intercept is at the origin. The trace in the \(xy\)-plane is the pair of lines \(y=\pm \dfrac{2}{3}x,\) which intersect at the origin. The traces parallel to the \(xy\)-plane are hyperbolas given by the equations \(\dfrac{x^{2}}{9}- \dfrac{y^{2}}{4}=k,\) where \(z=k.\)

The trace in the \(xz\)-plane is the parabola \(z=\dfrac{x^{2}}{9}\), which opens up. Traces parallel to the \(xz\)-plane are also parabolas that open up. The trace in the \(yz\)-plane is the parabola \(z=-\dfrac{y^{2}}{4},\) which opens down. Traces parallel to the \(yz\)-plane are also parabolas that open down.
The origin is the saddle point of the hyperbolic paraboloid. See Figure 68 for the graph.
NOW WORK
Problem 19.
3 Identify Cylinders
The three remaining quadric surfaces are called cylinders. Their standard equations are characterized by the fact that one of the variables is missing from the equation. In naming these surfaces, we have chosen \(z\) as the missing variable. As a result, \(z\) is an unrestricted variable, so these cylinders will be unbounded in the \(z\) direction.
Cylinders are surfaces that are generated by a line moving along a plane curve while remaining perpendicular* to the plane. Cylinders are named for the trace in the plane in which the unrestricted variable is \(0\); here, the \( xy\)-plane (\(z=0\)).
NOTE
Any of the three variables \(x\), \(y\), or \(z\) can be omitted. The corresponding graphs are unbounded in the direction of the missing variable.
*In general, the line moving along the plane curve can meet the curve at any constant angle. We only discuss cylinders for which this angle is 90\(^{\circ}\).
749
spanDEFINITIONspan Parabolic Cylinder
The graph of a parabolic cylinder has an equation of the form \[\bbox[5px, border:1px solid black, #F9F7ED] { \begin{array}{lll} x^{2}=4ay\qquad a\neq 0 \end{array} } \]

See Figure 69. This parabolic cylinder does not include the variable \(z\), so the trace in the \(xy\)-plane is the parabola \(x^{2}=4ay\). The surface is generated by moving a line along the parabola while remaining perpendicular to the plane containing the parabola. It can be visualized by taking a piece of paper and bending it so that an edge of the paper traces out a portion of a parabola.
spanDEFINITIONspan Elliptic Cylinder
The graph of an elliptic cylinder has an equation of the form \[\bbox[5px, border:1px solid black, #F9F7ED] { \begin{array}{lll} \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1 \qquad a\gt0, b\gt0 \end{array} } \]

See Figure 70. The trace of an elliptic cylinder in the \(xy\)-plane is an ellipse with its center at the origin. The surface is generated by moving a line along the ellipse \(\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1\) while remaining perpendicular to the plane containing the ellipse. An elliptic cylinder can be visualized by taking a piece of paper and attaching the two opposite edges in the shape of an ellipse.
If \(a=b\), then the trace in the \(xy\)-plane is a circle, and the cylinder is a right circular cylinder with radius \(a\).
spanDEFINITIONspan Hyperbolic Cylinder
The graph of a hyperbolic cylinder has an equation of the form \[\bbox[5px, border:1px solid black, #F9F7ED] { \begin{array}{lll} \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1\qquad a\gt0, b\gt0 \end{array} } \]
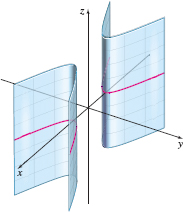
See Figure 71. The surface is generated by moving a line along one branch of the hyperbola \(\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1\) while remaining perpendicular to the plane containing the hyperbola and then repeating the procedure on the second branch. The intercepts are \(( \pm a,0,0)\). The hyperbolic cylinder consists of two parts, neither of which touches the \(z\)-axis. A hyperbolic cylinder can be visualized by bending two pieces of paper so that the curved edges trace out a portion of a hyperbola.
Identifying a Cylinder
Identify the cylinder defined by the equation \(y^{2}=8z\). Describe how it can be generated.
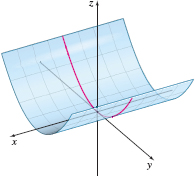
Solution \(y^{2}=8z\) is an equation of a parabolic cylinder. Since \( x \) is the missing variable, the cylinder is generated by moving a line that is perpendicular to the \(yz\)-plane along the parabola \(y^{2}=8z.\) See Figure 72
NOW WORK
Problem 23.
The quadric surfaces classified here are in standard position, with centers (or vertices) at the origin and symmetries with respect to the coordinate axes. When the center (or vertex) of a quadric surface is not located at the origin, but there is symmetry with respect to the lines parallel to the coordinate axes, a translation of axes may be applied to put the equation in standard form. The correct translation is obtained by completing squares. If the symmetry of the quadric surface is with respect to the lines that are not parallel to the coordinate axes, a rotation of axes, perhaps followed by a translation of axes, is required to put the equation in standard form.
750
Using rotations and translations, the list of nine basic equations provides an exhaustive classification of quadric surfaces. Rotations in space are somewhat involved and are not discussed here. However, the idea is quite similar to that of rotations in the plane.
4 Graph Quadric Surfaces
Quadrics are best graphed using a CAS. Comparing the given equation to those discussed in the section helps to identify the graph. Here are some suggestions to help make the comparison:
- Remember that the equations of the quadric surfaces listed are given in standard form. Interchanging the variables does not affect the classification; it only affects the orientation of the quadric surface. For example, \(z=\dfrac{x^{2}}{4}+\dfrac{y^{2}}{9}\) is the equation of an elliptic paraboloid whose graph lies above the \(xy\)-plane. The graph of \(y= \dfrac{x^{2}}{9}+\dfrac{z^{2}}{4}\) is also an elliptic paraboloid, but its graph lies to the right of the \(xz\)-plane.
- Cylinders are characterized by a variable missing from the equation. For example, the graph of the equation \(\dfrac{y^{2}}{4}+\dfrac{z^{2}}{9}=1\) is an elliptic cylinder perpendicular to the \(yz\)-plane.
- The technique of completing the square is sometimes required to identify the given quadric surface. In this case, a translation of axes will help to find the correct location of the graph.
Graphing Quadric Surfaces Using a CAS
![]() Identify each equation and use a CAS to obtain its graph.
Identify each equation and use a CAS to obtain its graph.
- \(4x^{2}-18y^{2}+9z^{2}=36\)
- \(4y^{2}+9z^{2}-36x^{2}=0\)
- \(x^{2}+z^{2}-4x=0\)
Solution
Divide both sides of the equation by \(36,\) obtaining \[ \frac{x^{2}}{9}-\frac{y^{2}}{2}+\frac{z^{2}}{4}=1 \]
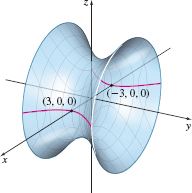 Figure 73 \(\dfrac{x^2}{9} - \dfrac{y^2}{2} + \dfrac{z^2}{4} =1\)
Figure 73 \(\dfrac{x^2}{9} - \dfrac{y^2}{2} + \dfrac{z^2}{4} =1\)This equation has three squared variables, one term negative, with \(1\) on the right, so it represents a hyperboloid of one sheet. Since the \(y\) term is negative, the \(y\)-axis is the axis of the hyperboloid of one sheet. See Figure 73.
The intercepts are \((3,0,0)\), \((-3,0,0)\), \((0,0,2)\), and \((0,0,-2)\). There are no \(y\)-intercepts.
The trace in the \(xz\)-plane is the ellipse \(\dfrac{x^{2}}{9}+\dfrac{z^{2}}{4} =1\), and all traces parallel to the \(xz\)-plane are also ellipses. The trace in the \(xy\)-plane is the hyperbola \(\dfrac{x^{2}}{9}-\dfrac{y^{2}}{2}=1\). The trace in the \(yz\)-plane is the hyperbola \(-\dfrac{y^{2}}{2}+\dfrac{z^{2} }{4}=1\). Traces parallel to the \(xy\)- and \(yz\)-planes are also hyperbolas. The \(y\)-axis is the axis of the hyperboloid of one sheet.
We begin by writing the equation as \[ \begin{equation*} x^{2}=\frac{y^{2}}{9}+\frac{z^{2}}{4} \end{equation*}
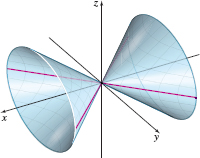 Figure 74 \(x^{2}=\dfrac{y^2}{9}+\dfrac{z^2}{4}\)
Figure 74 \(x^{2}=\dfrac{y^2}{9}+\dfrac{z^2}{4}\)Observe that the equation has three variables, all of which are squared, and no constant. This is the equation of an elliptic cone. See Figure 74.
751
The vertex of the cone is at the origin \(( 0,0,0) .\)
The trace of the elliptic cone in the \(yz\)-plane is the origin. Traces parallel to the \(yz\)-plane are ellipses centered on the \(x\)-axis. The trace in the \(xy\)-plane consists of the pair of intersecting lines \(x=\pm \dfrac{y }{3}\), and the trace in the \(xz\)-plane consists of the pair of intersecting lines \(x=\pm \dfrac{z}{2}\).
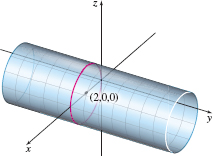 Figure 75 \(( x-2) ^{2}+z^{2}=4\)
Figure 75 \(( x-2) ^{2}+z^{2}=4\)Since the \(y\) variable is missing, the surface is a cylinder. To identify it, we complete the square in \(x\): \[ \begin{eqnarray*} x^{2}+z^{2}-4x &=&0 \\ ( x-2) ^{2}+z^{2} &=&4 \end{eqnarray*}
This is the equation of a right circular cylinder with a radius \(2\). The trace in the \(xz\)-plane is a circle of radius \(2\) and with its center at the point \( ( 2,0,0)\). See Figure 75.