Question

Opposite vertices of a rectangular box whose edges are parallel to the coordinate axes are (1, 0, 2) and (2, 3, 4). List the coordinates of the other six vertices of the box.

Question

Describe in words the set of all points \((x, y, z)\) that satisfy \(y=3\).

Question

The vector \(\mathbf{v}\) has initial point \(P_{1}=( 5, 0, -2)\) and terminal point \(P_{2}=( 7, 1, 3)\).

1. Write the vector \(\mathbf{v}\) in terms of its components.
2. Write the vector \(\mathbf{v}\) in terms of standard basis vectors.

Question

Find the magnitude of the vector \(\mathbf{v=}\) \(\mathbf{i}+2 \mathbf{j}+3\mathbf{k}\).

Question

Find the distance between the points \((1, 2, 3)\) and \((7, 5, 1)\).

Question

Write the equation of the sphere with center at the point \((1, 2, 3)\) and radius 4.

Question

Find the radius and center of the sphere: \(x^{2}+y^{2}+z^{2}-4x+8y=5\).

Question

If \(\mathbf{v}=\langle -2,-1,3\rangle \) and \(\mathbf{w} =\langle 5, 4, -2\rangle \), find \(3\mathbf{v}-2\mathbf{w}\).

Question

If \(\mathbf{v}=2\mathbf{i}+3\mathbf{j}-\mathbf{k}\) and \(\mathbf{w}=-\mathbf{i}-2\mathbf{j}+3\mathbf{k}\), find \(\Vert \mathbf{v}+\mathbf{w} \Vert \).

Question

Find a unit vector in the direction of \(\mathbf{v}=4\mathbf{i} +12\mathbf{j}-3\mathbf{k}\).

Question

Find a vector \(\mathbf{v}\) in the plane with magnitude \(25\) if the angle between \(\mathbf{v}\) and \(\mathbf{i}\) is \(120^\circ\).

Question

Find \(\mathbf{v}\) and \(\mathbf{w}\) if \[ \mathbf{w}-3\mathbf{v}=2\mathbf{i}+\mathbf{j}-\mathbf{k}\qquad\hbox{and}\qquad 2\mathbf{w}+\mathbf{v}=\mathbf{i}+\mathbf{j} \]

Question

1. Find the magnitude and direction cosines of the vector \(\mathbf{v}=5\mathbf{i}+8\mathbf{j}-2\mathbf{k}\).
2. Write \(\mathbf{v}\) in terms of its magnitude and direction cosines.

Question

Find the vector projection of \(\mathbf{v}=3\mathbf{i}+\mathbf{j} -2\mathbf{k}\) on \(\mathbf{w}=5\mathbf{i}-\mathbf{j}+\mathbf{k}\). Decompose \( \mathbf{v}\) into two vectors \(\mathbf{v}_{1}\) and \(\mathbf{v}_{2}\), where \( \mathbf{v}_{1}\) is parallel to \(\mathbf{w}\) and \(\mathbf{v}_{2}\) is orthogonal to \(\mathbf{w}\).

Question

Find the work done in moving an object along a vector \(\mathbf{u }=3\,\mathbf{i}+2\,\mathbf{j}-5\mathbf{k}\) if the applied force is \(\mathbf{F }=2\mathbf{i}-\,\mathbf{j}-\mathbf{k}\) . Use meters for distance and newtons for force.

Question

Three forces are applied to an object in mutually orthogonal directions: \(12\) units along the \(x\)-axis, \(16\) units along the \(y\)-axis, and \(15\) units along the \(z\)-axis. What is the resultant force?

Question

Find the angle between the vectors \(\mathbf{u}=\mathbf{i}+2 \mathbf{j}+3\mathbf{k}\) and \(\mathbf{v}=2\mathbf{i}-3\mathbf{j}-\mathbf{k}\).

Question

Find the angle at the vertex \(A\) of the triangle \(ABC\) with vertices \(A=(1, 0, 1)\), \(B=(2, -1, 1)\), and \(C=(-2, 1, 0)\).

Question

Find the distance between the parallel planes \[ \begin{array}{l@{\quad}rcl} p_{1} :& x+y-z&=&1 \\ p_{2} :& -2x-2y+2z&=&2 \end{array} \]

Question

A rigid body rotates with constant angular speed of \(\omega\) radians per second about a line through the origin and parallel to \(2\mathbf{ i}+3\mathbf{j}+6\mathbf{k}\). Find the speed of an object on this body at the instant it passes through the point \((1, 2, 3)\). Assume the distance is in meters.

Question

Find the line perpendicular to the lines \[ \begin{array}{lrcl@{\qquad}rcl@{\qquad}rcl} l: & \quad x&=&1-t, \quad & y&=&t, \quad & z&=&2t-1 \\ m: & \quad x&=&t+1, & y&=&-t, & z&=&t-1 \end{array} \]

Question

Find the line containing the point \((1, 2, 3)\) in the direction of \(\mathbf{v}=2\mathbf{i}-\mathbf{j}-4\mathbf{k}\).

Question

Find the scalar \(a\) so that \(\mathbf{v}=2\mathbf{i}-\mathbf{j} -4\mathbf{k}\) and \(\mathbf{w}=a\mathbf{i}+a\mathbf{j}+3\mathbf{k}\) are orthogonal.

Question

Find an equation of the sphere with \((2, 2, -3)\) and \((-2, 6, 5)\) as endpoints of a diameter. Graph the sphere.

Question

Find the line of intersection of the two planes \(p_{1}\): \( x-y+z=3\) and \(p_{2}\): \(2x+2y-z=1.\)

Question

Find an equation of the plane with nonzero intercepts \((a, 0, 0)\) , \((0, b, 0)\), \((0, 0, c)\).

Question

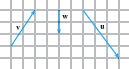
Use the vectors in the figure to graph each of the following vectors:

1. \(( 2+3) \mathbf{v}\)
2. \(2( \mathbf{u-w})\)
3. \(( \mathbf{u+v}) +\mathbf{w}\)
4. \(\mathbf{v}+( -\mathbf{v})\)
5. \(\mathbf{u}-3\mathbf{v}\)

Question

Determine whether the lines \(l_{1}\) and \(l_{2}\) intersect, are parallel, or are skew. \[ \begin{array}[t]{ll} l_{1}\hbox{:}~ & ~\dfrac{x+5}{6}=\dfrac{y-2}{3}=\dfrac{z+4}{7} \\ l_{2}\hbox{:}~ & ~\dfrac{x+5}{6}=\dfrac{y+1}{3}=\dfrac{z-2}{7} \end{array} \]

Question

Find the general equation of the plane containing the point \( ( 2, -1, 4)\) and normal to the line \(\dfrac{x+3}{2}=\dfrac{y-3}{3} =z\).

Question

Determine whether the lines \(l_{1}\) and \(l_{2}\) intersect, are parallel, or are skew. \[ \begin{equation*} \begin{array}{ll} l_{1}\hbox{:}&x=t+1,\qquad y=3t,\qquad z=t-1 \\ l_{2}\hbox{:}&\dfrac{x+3}{2}=\dfrac{y-3}{3}=z \end{array} \end{equation*}\]

Question

Find a line normal to the plane containing the lines \[ \begin{equation*} x-2=\frac{y+1}{2}=\frac{z-1}{2}\qquad \hbox{and }\qquad x+1=\frac{y+8}{3}= \frac{z}{-3} \end{equation*}\]

at their point of intersection.

Question

Find the line containing the points \(P_{1}=( 4,0,7) \) and \(P_{2}=( 5,3,6)\).

Question

\(\dfrac{x^{2}}{4}-\dfrac{y^{2}}{9}=1\)

Question

\(x^{2}+y^{2}-\dfrac{z^{2}}{4}=-1\)

Question

\(z=\dfrac{x^{2}}{4}-\dfrac{y^{2}}{9}\)

Question

\(z^{2}=\dfrac{x^{2}}{4}+\dfrac{y^{2}}{9}\)

Question

\(\dfrac{x^{2}}{4}+\dfrac{y^{2}}{9}+z^{2}=1\)