CHAPTER 10 PROJECT The Hall Effect

While investigating the effects of magnets on electric current in 1879, E. H. Hall observed a phenomenon that is now used to measure the density of electric charge carriers in semiconductors. The so-called Hall effect describes the creation of a voltage, or potential difference, on opposite sides of a conductor in the presence of an external magnetic field, created when an electric current flows through it. The magnetic field exerts a force on the moving carriers that tends to push them to one side of the conductor. The buildup of charges at the sides of the conductor balances the magnetic influence and produces a voltage between the two sides of the conductor.

The geometry of this situation is based on the relationships among the initial velocity \(\mathbf{v}_{0}\) of the charges, the magnetic field \( \mathbf{B}\), and the resulting magnetic force \(\mathbf{F}_{\mathbf{m}}\) on the charges.

When an electric charge \(q\) moves in the presence of a magnetic field, it experiences a magnetic force given by \(\mathbf{F}_{\bf m}=q\mathbf{v}\times \mathbf{B}\). Note that because the magnetic force is proportional to the cross product of the velocity \(\mathbf{v}\) and the magnetic field \(\mathbf{B} \), it must be orthogonal to each of these vectors. This relationship is illustrated in Figure 76.

Assuming \(q\) has a positive charge, the velocity \(\mathbf{v}\) is in the \(\mathbf{j}\) direction, and the magnetic field \(\mathbf{B}\) is in the \(\mathbf{k}\) direction, then the resulting force \(\mathbf{F}_{\mathbf{m}}\) is in the \(\mathbf{i}\) direction.

1. Given the velocity and magnetic field shown in Figure 76, in what direction would the magnetic force point if \(q\) has a negative charge?

   

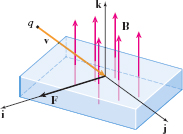   Figure 76

   As charges continue to flow into the region of the magnetic field, they are deflected toward the side of the conductor in the direction of the magnetic force and collect there. At the same time, the opposite side of the material can be thought of as being deficient in the amount of charge carriers. This creates a voltage, or potential difference, between the two sides. A consequence of this is that a static electric field is created within the conductor. In the example depicted in Figure 76, the electric field \(\mathbf{E}\) would point in the \(-\mathbf{i}\) direction, as positive charges collect on the side of the material in the direction of \(\mathbf{F}_{\mathbf{m}}\). See Figure 77. Note that the magnetic field is still present as charges continue to build up and make the electric field stronger and stronger.

   

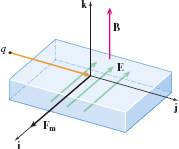   Figure 77 The polarity resulting from positive charge carriers, as happens in many semiconductors.

   You might ask, “Won’t this electric field just keep increasing as charges continue to flow through the conductor and are deflected by the magnetic field?” This would be true if not for a competing effect—the electric field itself. The charges also experience an electric force, \(\mathbf{F}_{\mathbf{e}}\), as the electric field \(\mathbf{E}\) is created and becomes stronger. The electric force on a charge in an electric field is given by the relationship \(\mathbf{F}_\mathbf{e}=q\mathbf{E}\). Note that the electric force on a positive charge would be in the same direction as the electric field and the directions of the magnetic and electric forces are opposed. Then as the electric field increases, subsequent charges moving into the material experience less and less of a net force, until the electric field becomes strong enough that subsequent charges experience no net force at all. When this happens, the potential difference across the conductor is established (by the electric field) and is measured. This potential difference is often referred to as the Hall voltage for the conductor.

2. A stream of electrons, each with a charge \(q=-1.6\times 10^{-19} \text{C}\), have an initial velocity \(\mathbf{v}_{0}\) in meters per second (\(\text {m}/\text{s}\)) of \(\mathbf{v}_{0}=( 1.0\times 10^{-4}) \mathbf{i}+( 2.0\times 10^{-4}) \mathbf{j}-( 4.0\times 10^{-4}) \mathbf{k}\). The charges move along the length of a semiconducting material and enter a region of magnetic field measured in teslas (\(\text{T}\)) with \(\mathbf{B}=0.5\mathbf{i}+1.0\mathbf{j}+0.625\, \mathbf{k}.\) Find the magnitude of the initial velocity and the magnetic field.
3. Find unit vectors in the direction of the velocity and the magnetic field.
4. Verify that the velocity \(\mathbf{v}\) and the magnetic field \( \mathbf{B}\) are orthogonal, as required for the Hall effect.
5. Find the magnetic force \(\mathbf{F}_{\mathbf{m}}\) on the electrons as they enter the region of the magnetic field. The units of the magnetic force are newtons (\(\text{N}\)).
6. The electric force \(\mathbf{F}_{\mathbf{e}}\) will grow until it is finally equal in magnitude to the magnetic force \(\mathbf{F}_{\mathbf{m}}\) but in the opposite direction. Write an expression for the final electric force. What are the units of the electric force?
7. Find the electric field \(\mathbf{E}\) responsible for the electric force \(\mathbf{F}_{\mathbf{e}}\) found in Problem 6. Verify that \( \mathbf{E}\) points in one of the two possible directions found in Problem 6. What are the units of the electric field?