10.1 Rectangular Coordinates in Space

Printed Page 695

A two-dimensional rectangular coordinate system is represented by a plane in which every point $P$ corresponds to exactly one ordered pair of real numbers $( x,\,y) ,$ the coordinates of $P.$ In space every point $P$ corresponds to exactly one ordered triple of real numbers $( x,y,z)$.

1 Locate Points in Space

Printed Page 695

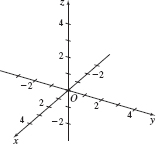
We begin by selecting a fixed point called the origin $O$. Through the origin, draw three mutually perpendicular number lines, called the coordinate axes. The coordinate axes are usually labeled the ${x}$-axis the ${y}$-axis and the ${z}$-axis. On each axis choose one direction as positive and select an appropriate scale, as shown in Figure 1.

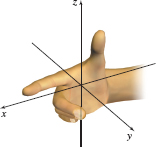
Notice label in Figure 1 that the positive $z$-axis points upward, the positive $y$-axis points toward the right, and the positive $x$-axis points forward. This is known as a right-handed system because it conforms to the right-hand rule. The right-hand rule states: if the index finger of the right hand points in the direction of the positive $x$-axis and the other fingers point in the direction of the positive $y$-axis, then the thumb will point in the direction of the positive $z$-axis, as shown in Figure 2.

As in the plane, we assign coordinates to each point $P$ in space, but in space we use an ordered triple of real numbers $( x,\,y,\,z)$. For example, the point $( 3,5,7)$, is the point for which $3$ is the $x$-coordinate, $5$ is the $y$-coordinate, and $7$ is the $z$-coordinate. The point $( 3,5,7)$ is plotted by starting at the origin, moving 3 units along the positive $x$-axis, $5$ units in the direction of the positive $y$-axis, and $7$ units in the direction of the positive $z$-axis. See Figure 3.

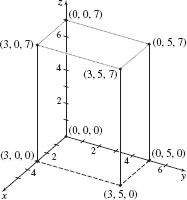
Figure 3 also shows the points $( 3,0,0)$, $(0,5,0)$, $(0,0,7)$, $(3,5,0)$, $( 3,0,7)$, $0,5,7)$ and $(0,0,0),$ which form a box with the points $(0,0,0)$ and $( 3,5,7)$ as opposite vertices.

Points of the form $( x,0,0)$ lie on the $x$-axis, while points of the form $( 0,y,0)$ and $( 0,0,z)$ lie on the $y$-axis and $z$-axis, respectively.

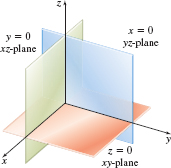
Points of the form $(x,y,0)$ lie on a plane called the $xy$-plane. The $xy$-plane is perpendicular to the $z$-axis and its equation is $z =0$. This is the plane used in the familiar two-dimensional rectangular coordinate system.

Points of the form $( x,0,z)$ lie on the $xz$-plane. The $xz$-plane is perpendicular to the $y$-axis, and its equation is $y=0$. Finally, points of the form $( 0,y,z)$ lie on the $yz$-plane, which is perpendicular to the $x$-axis, and its equation is $x=0$. Collectively, these three planes are referred to as coordinate planes. See Figure 4.

In general, for any real number $k$, the graph of $x=k$ is a plane parallel to the $yz$-plane; the graph of $y=k$ is a plane parallel to the $xz$-plane; and the graph of $z=k$ is a plane parallel to the $xy$-plane. As shown in Figure 5, the graph of the equation $z=5$ is a plane parallel to and $5$ units above the $xy$-plane.

2 Find the Distance Between Two Points in Space

Printed Page 696

The formula for the distance between two points in space is an extension of the distance formula in the plane.

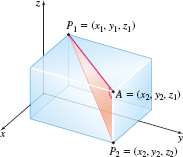
To find the distance $|P_{1}~P_{2}|$ between two points $P_{1}=(x_{1},y_{1},z_{1})$ and $P_{2}=(x_{2},y_{2},z_{2})$, we use the Pythagorean Theorem twice. Figure 6 shows the points $P_{1}$ and $P_{2}$ and a third point $A=(x_{2},y_{2},z_{1})$. The first application of the Pythagorean Theorem involves observing that the triangle $P_{1}~A~P_{2}$ is a right triangle where the side of length $|P_{1}~P_{2}|$ is the hypotenuse. As a result, $$\left\vert P_{1}~P_{2}\right\vert =\sqrt{\vert P_{1}~A\vert ^{2}+\vert A~P_{2}\vert ^{2}}\qquad{\color{#0066A7}{\hbox{Pythagorean Theorem}}}$$

The points $P_{1}$ and $A$ lie in a plane parallel to the $xy$-plane. Do you see why? To find $\left\vert P_{1}~A\right\vert$, we use the distance formula in the plane: $$\begin{equation*} \left\vert P_{1}\,A\right\vert =\sqrt{( x_{2}-x_{1}) ^{2}+( y_{2}-y_{1}) ^{2}} \end{equation*}$$

The points $P_{2}$ and $A$ lie on a line parallel to the $z$-axis, so that $\left\vert A~P_{2}\right\vert =\left\vert z_{2}-z_{1}\right\vert$ and $\left\vert A~P_{2}\right\vert ^{2}=(z_{2}-z_{1})^{2}.$ Combining these results, we obtain a formula for the distance between two points in space.

3 Find the Equation of a Sphere

Printed Page 697

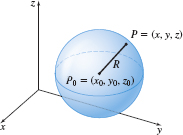
The collection of all points in space that are a fixed distance $R$ from a fixed point $P_{0}=( x_{0},y_{0},z_{0})$ is called a sphere. See Figure 7. The fixed distance $R$ is called the radius, and the fixed point $P_{0}$ is called the center of the sphere. The distance from any point $P=(x, y, z)$ on a sphere of radius $R$ to the center point $P_{0}=(x_{0},y_{0},z_{0})$ is $\vert PP_{0}\vert=R$. The Distance Formula in space shows that $$\begin{equation*} \vert P\!P_{0}\vert =\sqrt{ (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}}=R \end{equation*}$$

Squaring both sides gives the standard form of the equation of a sphere.