10.3 Assess Your Understanding
Concepts and Vocabulary
Question
In space, the standard basis vectors are \(\mathbf{i} = \) _____, \(\mathbf{j} =\) _____, and \(\mathbf{k}\) = _____.
Question
A vector whose magnitude is 1 is called a(n) _____ vector.
Question
\(v_{1},\) \(v_{2},\) and \(v_{3}\) are called the _____ of \(\mathbf{v} = \langle v_{1},v_{2},v_{3}\rangle \).
Question
True or False If \(\mathbf{w} = 4 \mathbf{v}\), then \( \mathbf{w}\) has the same direction as \(\mathbf{v}\).
Question
True or False The magnitude of a vector is found by adding its components.
Question
True or False In the plane, if the angle between a nonzero vector \(\mathbf{v}\) and the unit vector \(\mathbf{i}\) is \(\theta,\) then \(\mathbf{v} = \Vert\mathbf{v}\Vert (\cos \theta \mathbf{i} + \sin \theta \mathbf{j}).\)
Question
If \(\mathbf{v} = \mathbf{i} + \mathbf{j} + \mathbf{k},\) the unit vector \(\mathbf{u}\) in the direction of \(\mathbf{v}\) is \(\mathbf{u}\) = _____.
Question
True or False For a vector \(\mathbf{v}\) in the plane, \(\Vert -2\, \mathbf{v} \Vert = -2 \Vert\mathbf{v} \Vert\)
Skill Building
In Problems 9–16, the vector \(\mathbf{v}\) has initial point \(P_{1}\) and terminal point \(P_{2}\).
- Write each vector \(\mathbf{v}\) as a position vector.
- Write each vector \(\mathbf{v}\) in terms of the standard basis vectors.
Question
\(P_{1} = (2,3)\) and \(P_{2} = (6,-2)\)
Question
\(P_{1} = (4,-1)\) and \(P_{2} = (-3,2)\)
Question
\(P_{1} = (0,5)\) and \(P_{2} = (-1,6)\)
Question
\(P_{1} = (-2,0)\) and \(P_{2} = (3,2)\)
Question
\(P_{1} = (6,2,1)\) and \(P_{2} = (3,0,2)\)
Question
\(P_{1} = (4,7,0)\) and \(P_{2} = (0,5,6)\)
Question
\(P_{1} = (-1,0,1)\) and \(P_{2} = (2,0,0)\)
Question
\(P_{1} = (6,2,2)\) and \(P_{2} = (2,6,2)\)
In Problems 17–24, use \(\mathbf{v}\) = \(\langle 3,-1\rangle\) and \(\mathbf{w}\) = \(\langle -3,2\rangle\) to find each quantity.
Question
\(2\mathbf{v}-\mathbf{w}\)
Question
\(\mathbf{v}+5\mathbf{w}\)
Question
\(\dfrac{1}{3} \mathbf{v}+\dfrac{1}{2}\mathbf{w}\)
Question
\(\dfrac{2}{3}\mathbf{v}-\dfrac{1}{2}\mathbf{w}\)
Question
\(\left\Vert \mathbf{v}\right\Vert \)
Question
\(\left\Vert \mathbf{w}\right\Vert\)
Question
\(\Vert 2\,\mathbf{v}-\mathbf{w}\Vert \)
Question
\(\Vert \mathbf{v}+\mathbf{w}\Vert \)
In Problems 25–32, use \(\mathbf{u}\) = \(\langle 1,1,-6\rangle,\) \(\mathbf{v}\) = \(\langle 3,0,8\rangle,\) and \(\mathbf{w}\) = \(\langle -3,-1,2\rangle\) to find each quantity.
Question
\(3\mathbf{v}-2\mathbf{w}\)
Question
\(-2\mathbf{v}+\mathbf{w}\)
Question
\(2\mathbf{u}-3\mathbf{v}+4\mathbf{w}\)
Question
\(\mathbf{u} + 3\left( \mathbf{v} - 4\mathbf{w}\right)\)
Question
\(\Vert\mathbf{u}\Vert\)
Question
\(\Vert \mathbf{v}\Vert \)
Question
\(\Vert 5\mathbf{u} - \mathbf{v} + \mathbf{w}\Vert \)
Question
\(\Vert 5\mathbf{u}\Vert -\Vert \mathbf{v}\Vert +\Vert \mathbf{w}\Vert \)
In Problems 33–42, find the magnitude of each vector \(\mathbf{v}\).
Question
\(\mathbf{v} = 4\mathbf{i} - 3\mathbf{j}\)
Question
\(\mathbf{v} = \mathbf{i}-12 \mathbf{j}\)
Question
\(\mathbf{v} = \mathbf{i} + \mathbf{j}\)
Question
\(\mathbf{v} = \mathbf{i}-\mathbf{j}\)
Question
\(\mathbf{v} = 4\mathbf{i} + 2\mathbf{j} - \mathbf{k}\)
Question
\(\mathbf{v} = \mathbf{i} - \mathbf{j} + \mathbf{k}\)
Question
\(\mathbf{v} = \mathbf{j} + \mathbf{k}\)
Question
\(\mathbf{v} = 2\mathbf{i} - \mathbf{k}\)
Question
\(\mathbf{v} = (\cos \theta)\mathbf{i} + (\sin \theta) \mathbf{j}\)
Question
\(\mathbf{v} = (\cos \theta ) \mathbf{i} + (\sin \theta) \mathbf{j} + \mathbf{k}\)
In Problems 43–54, normalize each vector \(\mathbf{v}\). What is the unit vector in the opposite direction of \(\mathbf{v}\)?
Question
\(\mathbf{v} = \langle 5,12\rangle \)
Question
\(\mathbf{v} = \langle 3,4\rangle \)
Question
\(\mathbf{v} = 2\mathbf{i} + \mathbf{j}\)
Question
\(\mathbf{v}=\mathbf{i}-\mathbf{j}\)
Question
\(\mathbf{v} = \dfrac{1}{2}\mathbf{i} + \dfrac{\sqrt{3}}{2}\mathbf{j}\)
Question
\(\mathbf{v} = \dfrac{\sqrt{2}}{2}(\mathbf{i} - \mathbf{j})\)
Question
\(\mathbf{v} = \langle 1,1,1\rangle\)
Question
\(\mathbf{v} = \langle 1,-1,-1\rangle \)
Question
\(\mathbf{v} = (\cos \theta) \mathbf{i} + (\sin\theta) \mathbf{j} + 2\sqrt{2} \mathbf{k}\)
Question
\(\mathbf{v} = (\sin \theta) \mathbf{i} + (\cos \theta) \mathbf{j} + \mathbf{k}\)
Question
\(\mathbf{v} = 3\mathbf{i}-4\mathbf{j} + 12\mathbf{k}\)
Question
\(\mathbf{v} = \dfrac{1}{2} \mathbf{i} - \dfrac{1}{2} \mathbf{j} + \dfrac{\sqrt{2} }{2} \mathbf{k}\)
713
In Problems 55–60, use \(\mathbf{v} = 2\mathbf{i} - 3\mathbf{j}\) and \(\mathbf{w}\) = \(\mathbf{i} + 2\mathbf{j}\) to find the indicated quantity.
Question
\(2\mathbf{v} - \mathbf{w}\)
Question
\(\mathbf{v} + 5\mathbf{w}\)
Question
\(\dfrac{1}{3}\mathbf{v} + \dfrac{1}{2}\mathbf{w}\)
Question
\(\dfrac{2}{3}\mathbf{v} - \dfrac{1}{2}\mathbf{w}\)
Question
\(\Vert \mathbf{v} - \mathbf{w}\Vert \)
Question
\(\left\Vert \mathbf{v} + \mathbf{w}\right\Vert \)
In Problems 61–70, use \(\mathbf{u}\) = \(\mathbf{i} - 2\mathbf{j} + 3 \mathbf{k}\), \(\mathbf{ v} = 3\mathbf{i} + \mathbf{j} - \mathbf{k}\) , and \(\mathbf{ w} = 6\mathbf{i}\) + \(\mathbf{ j}\) + \(\mathbf{k}\) to find the indicated quantity.
Question
\(3\mathbf{v}-2\mathbf{w}\)
Question
\(-2\mathbf{v}+\mathbf{w}\)
Question
\(2\mathbf{u}-3\mathbf{v}+4 \mathbf{w}\)
Question
\(5\mathbf{u}-\mathbf{v}+\mathbf{w}\)
Question
\(\Vert \mathbf{v}-\mathbf{w}\Vert\)
Question
\(\Vert 2\mathbf{v}+\mathbf{w}\Vert \)
Question
\( \Vert \mathbf{u}\Vert +\Vert \mathbf{v}\Vert +\Vert \mathbf{w}\Vert \)
Question
\(\Vert \mathbf{u}+\mathbf{v}+\mathbf{w}\Vert \)
Question
\(\dfrac{\mathbf{u}+\mathbf{v}}{\Vert \mathbf{w\Vert }}\)
Question
\(\dfrac{\mathbf{u}}{\Vert \mathbf{v}+\mathbf{w}\Vert }\)
In Problems 71–76, determine whether the vectors \(\mathbf{v}\) and \(\mathbf{w}\) are parallel. If the vectors are parallel, are their directions the same or opposite?
Question
\(\mathbf{v} = 2\mathbf{i} + 3\mathbf{j},\quad\) \(\mathbf{w} = 3 \mathbf{i} + \dfrac{9}{2} \mathbf{j}\)
Question
\(\mathbf{v} = 3\mathbf{i} + 2\mathbf{j},\quad\) \(\mathbf{w} = 6\mathbf{i} - 4\mathbf{j}\)
Question
\(\mathbf{v} = \langle 2,6,-12\rangle, \quad\) \(\mathbf{w} = \langle -1,-3,4\rangle \)
Question
\(\mathbf{v} = \langle \sqrt{2},1,3\rangle, \quad\) \(\mathbf{w} = \langle 2,1,9\rangle \)
Question
\(\mathbf{v} = \langle 12,3,-9\rangle, \quad\) \(\mathbf{w} = \langle -4,-1,3\rangle \)
Question
\(\mathbf{v} = \langle -6,8,2\rangle, \quad\) \(\mathbf{w} = \langle -3,4,0\rangle \)
Applications and Extensions
Question
Find a vector whose magnitude is \(4\) that is parallel to \(2 \mathbf{i}-3\mathbf{j}+4\mathbf{k}\).
Question
Find a vector whose magnitude is \(2\) that is parallel to \(- \mathbf{i}+\mathbf{j}+2\mathbf{k}\).
Question
Find \(a\) so that the vectors \(2\mathbf{i}+\mathbf{j}-\mathbf{k }\) and \(2a\,\mathbf{i}+\mathbf{j}+\mathbf{k}\) have the same magnitude.
Question
Find \(a\) so that \(\Vert a\,\mathbf{i}+(a+1)\,\mathbf{j}+2 \mathbf{k}\Vert =3\).
Question
If \(\mathbf{v}=2\mathbf{i}+\mathbf{j}\) and \(\mathbf{w}=x\, \mathbf{i}+3\,\mathbf{j}\), find all numbers \(x\) so that \(\Vert \mathbf{v}+ \mathbf{w}\Vert =5\).
Question
A vector \(\mathbf{v}\) has initial point \(P_{1}=(-3, 1)\) and terminal point \(P_{2}=(x, 4).\) Find all numbers \(x\) so that \(\mathbf{v}\) has length \(5.\)
In Problems 83–88, find all vectors \(\mathbf{v}\) = \(a \mathbf{i}\) + \(b \mathbf{j}\) that have the indicated properties.
Question
Magnitude of \(\mathbf{v}\) is \(4\); \(\mathbf{v}\) makes an angle of \(30^{\circ }\) with the positive \(x\)-axis.
Question
Magnitude of \(\mathbf{v}\) is \(2\); \(\mathbf{v}\) makes an angle of \(45^{\circ }\) with the positive \(x\)-axis.
Question
Magnitude of \(\mathbf{v}\) is \(5\); the \(\mathbf{i}\) component is twice the \(\mathbf{j}\) component.
Question
Magnitude of \(\mathbf{v}\) is \(5\); the \(\mathbf{i}\) component equals the \(\mathbf{j}\) component.
Question
The \(\mathbf{j}\) component of \(\mathbf{v}\) is \(1\); \(\mathbf{v} \) makes an angle of \(135^{\circ }\) with the positive \(x\)-axis.
Question
The \(\mathbf{i}\) component of \(\mathbf{v}\) is \(-3\); \( \mathbf{v}\) makes an angle of \(210^{\circ }\) with the positive \(x\)-axis.
Question
Acceleration A force \(\mathbf{\ F}=10\mathbf{i}-15\mathbf{j} + 25\mathbf{k}\), measured in newtons N, is applied to an object of mass \(10~\text{kg},\) causing it to accelerate in the direction of \(\mathbf{F}\). Find the magnitude of the acceleration of the object (in newtons per kilogram).
Question
Computer Graphics In computer graphics, vectors are used to translate points. For example, if the point \((-3,2) \) is translated by the vector \(\mathbf{v} = \langle 5,2\rangle\), then the new location will be \(\mathbf{u}^{\prime } = \mathbf{u + v =} \langle -3,2\rangle + \langle 5,2\rangle = \langle 2,4\rangle,\) as shown in the figure.
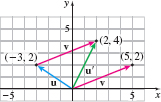
Source: Phil Dadd. Vectors and matrices: A primer. http://www.gamedev.net/reference/articles/article1832.asp.
- Determine the new coordinates of \((3,-1) \) if it is translated by \(\mathbf{v} = \langle -4,5\rangle.\)
- Illustrate the translation graphically.
Question
Computer Graphics The points \((-3,0),\) \((-1,-2),\) \((3,1) ,\) and \((1,3) \) are the vertices of a parallelogram ABCD.
- If ABCD is translated by \(\mathbf{v} = \langle 3,-2\rangle,\) find the vertices of the new parallelogram \(A^{\prime}B^{\prime }C^{\prime }D^{\prime }\).
- If ABCD is translated by \(\dfrac{1}{2}\mathbf{v},\) find the vertices of the new parallelogram \(A^{\prime }B^{\prime }C^{\prime }D^{\prime }\).
Question
Ground Speed of an Airplane An airplane has an air speed of 500 km/h in an easterly direction. If there is a southeast wind of 60 km/h, find the speed of the airplane relative to the ground.
Question
Position of an Airplane An airplane travels \(200\) mi due west and then travels 150 mi in a direction \(60{{}^\circ}\) north of west. Find the vector that gives the position of the airplane.
Question
Average Air Speed of an Airplane An airplane, after 1 h of flying, arrives at a point 200 mi due south of the departure point. If, during the flight, there was a steady northwest wind of 20 mi/h, what was the airplane’s average air speed?
Question
Static Equilibrium Forces \(\mathbf{F}_{1},\mathbf{F}_{2}, \mathbf{F}_{3},\mathbf{F}_{4}\) act on an object \(Q\) as shown in the figure. Draw the force \(\mathbf{F}\) needed to prevent \(Q\) from moving.

Question
Overcoming a Force Two friends are trying to pull a car out of a ditch. They apply forces, measured in pounds, of \(\mathbf{F}_{1} = 200 \mathbf{i} + 350\mathbf{j} + 100\mathbf{k}\) and \(\mathbf{F}_{2} = 250\mathbf{i} + 300\mathbf{j} + 150\mathbf{k}\), respectively, to the car, but it does not move. Find the third force \(\mathbf{F}_{3}\), due to the mud and ground, acting on the car and preventing it from moving.
714
Question
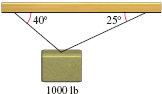
Static Equilibrium A weight of 1000 lb is suspended from two cables, as shown in the figure. What is the tension in each cable?
Question
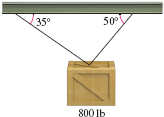
Static Equilibrium A weight of 800 lb is suspended from two cables attached to a horizontal steel beam, as shown in the figure. What is the tension in each cable?
Question
Tug of War Three pieces of rope are knotted together for use in a three-team tug of war. Each rope is pulled parallel to the ground. As viewed from above, Team A pulls with a force of \(1100~\text{lb}\) at an angle of \(0{{}^\circ}\), Team B pulls with a force of \(1050~\text{lb}\) at an angle of \(120{{}^\circ},\) and Team C pulls with a force of \(1000~\text{lb}\) at an angle of \(240{{}^\circ}.\)
- Draw a force diagram representing the forces acting on the knot.
- Find the net force acting on the knot.
Question
Pushing a Wheelbarrow A man pushes a wheelbarrow up an incline of 20\(^{\circ}\) to the ground with a force of 100 lb. Represent graphically this force.
Question
Pulling a Wagon A child pulls a wagon with a force of \(40\) lb. The handle of the wagon makes an angle of 30\(^{\circ}\) with the ground. Represent graphically this force.
Question
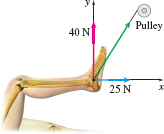
Orthopedics A patient with a broken tibia has the lower half of his leg suspended horizontally by a cable attached to the center of his foot. See the figure. The tension in the cable needs to exert a force of \(25~\text{N}\) horizontally for traction and \(40~\text{N}\) vertically upward to support the leg. Find the tension in the cable.
(Hint: Put the center of the patient’s foot at the origin of an \(xy\)-plane.)
Question
Chemistry: Gold Crystals In its solid form, gold forms a crystal lattice known as a face-centered cubic (fcc). The crystal consists of eight gold atoms at the corners of a cube plus six more atoms, one at the center of each face of the cube, as shown in the figure. The sides of the cube are 0.408nm long (1nm = 10-9m). Put one corner of the cube at the origin, and place three of the faces along the positive coordinate planes.
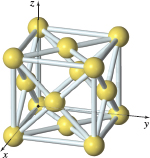
- Assign coordinates to each atom in the crystal.
- Find a vector that represents each of the following atoms:
- The atom furthest from the origin
- The atom in the center of the cube face that is parallel to the \( xz\)-plane, but not in that plane
- The atom in the center of the cube face that is parallel to the \(xy\)-plane, but not in that plane
- What is the magnitude of each of the vectors found in (b)?
Question
Theoretical Speed An airplane travels in a northeasterly direction at 250 km/h relative to the ground, due to the fact that there is an easterly wind of 50 km/h relative to the ground. How fast would the plane be going if there were no wind?
Question
Wind Velocity A woman on a bike traveling east at 8 mi/h finds that the wind appears to be coming from the north. Upon doubling her speed, she finds that the wind appears to be coming from the northeast. Find the velocity of the wind.
Question
Show that the properties of vector addition and scalar multiplication (p. 706) hold for vectors in the plane.
Question
Show that the properties of vector addition and scalar multiplication (p. 706) hold for vectors in space.
Question
Show that if \(a\) is scalar and \(\mathbf{v}\) is a vector, then \(\Vert a \mathbf{v}\Vert = |a| \Vert \mathbf{v}\Vert \) for vectors in space.
Question
Show that every vector \(\mathbf{v} = \langle v_{1},v_{2}, v_{3}\rangle\) in space can be written in terms of the vectors \( \mathbf{i}\), \(\mathbf{j}\), and \(\mathbf{k}\) as \(\mathbf{v} = v_{1}\,\mathbf{i} + v_{2} \mathbf{j} + v_{3} \mathbf{k}.\)
Challenge Problems
Question
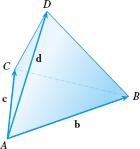
Geometry Let A, B, C, and D be the vertices of a tetrahedron (triangular pyramid) in space. Let \(\mathbf{b}=\overrightarrow {\it AB}\), \(\mathbf{c} = \overrightarrow {\it AC}\), and \(\mathbf{d} = \overrightarrow{\it AD}\). Express the directed edges \(\overrightarrow {\it BC},\overrightarrow {\it BD},\) and \( \overrightarrow {\it CD}\) of the tetrahedron in terms of the vectors \(\mathbf{b}, \mathbf{c},\) and \(\mathbf{d}\).
Question
Geometry Let \(A,B,C,D,E,F,G,\) and \(H\) be the vertices of a parallelepiped in space, whose faces are the parallelograms ABCD, ABFE, AEHD, and so forth. Let \(\mathbf{b} = \skew5\overrightarrow {\it AB}, \mathbf{e} = \overrightarrow{\it AE},\) and \(\mathbf{d} = \overrightarrow {\it AD}\). Express the vectors \(\overrightarrow {\it AC}, \overrightarrow {\it AF}, \overrightarrow {\it AG},\overrightarrow {\it FG},\) and \(\overrightarrow {\it EG}\) in terms of \(\mathbf{b},\mathbf{e},\) and \(\mathbf{d}\).
Question
Let points \(P_{1}=(x_{1},y_{1},z_{1})\) and \( P_{2} = (x_{2},y_{2},z_{2})\) have respective position vectors \(\mathbf{r} _{1}\) and \(\mathbf{r}_{2}\). Show that the point \(P = (x,y,z)\) that divides the segment \(P_{1}~P_{2}\) in the ratio \(t = \dfrac{\overline{P_{1}P}}{\overline{ P_{1}~P_{2}}}\) has position vector \(\mathbf{r} = \mathbf{r}_{1} + t(\mathbf{r} _{2} - \mathbf{r}_{1})\). From this, conclude that \[ \begin{eqnarray*} x & =& x_{1}+t(x_{2}-x_{1}) \\ y & =& y_{1}+t(y_{2}-y_{1}) \\ z & =& z_{1}+t(z_{2}-z_{1}) \end{eqnarray*}\]
715
Question
Let \(\mathbf{u}\) and \(\mathbf{v}\) be two nonparallel, nonzero vectors in the plane. Show that for each vector \(\mathbf{w}\) there exist unique scalars \(s\) and \(t\) so that \(\mathbf{w}=s\mathbf{u}+t\mathbf{v}\). Interpret the result geometrically.
