Question

True or False To integrate a vector function \( \mathbf{r=r}( t), \) integrate each component individually.

Question

True or False When integrating a vector function \(\mathbf{r=r}(t), \) there is no need to add a constant of integration.

Question

\(\int (\sin t\mathbf{i}-\cos t\mathbf{j}+t\mathbf{k})dt\)

Question

\(\int (\cos t\mathbf{i}+\sin t\mathbf{j}-\mathbf{k})dt\)

Question

\(\int (t^{2}\mathbf{i}-t\mathbf{j}+e^{t}\mathbf{k})dt\)

Question

\(\int (e^{t}\mathbf{i}-\sqrt{t}\mathbf{j}+t^{2}\mathbf{k})dt\)

Question

\(\int ( \ln t\mathbf{i}-t\ln t\mathbf{j}-2\mathbf{k}) dt\)

Question

\(\int \left( \mathbf{i}+\ln t\mathbf{j}+\dfrac{1}{t}\mathbf{k}\right) dt\)

Question

\(\int [ ( t-2) \mathbf{i}-( t-2) ^{2}\mathbf{j}+\mathbf{k}] dt\)

Question

\(\int [ ( 3t+1) \mathbf{i}+( 3t+1) ^{2}\mathbf{j} +( 3t+1) ^{-1}\mathbf{k}] dt\)

Question

\(\mathbf{r}^{\prime} ( t)\;=\;e^{t}\mathbf{i}-\ln t\mathbf{j}+2t\mathbf{k,}\;\mathbf\quad{r}(1)=\mathbf{j}+\mathbf{k}\)

Question

\(\mathbf{r}^{\prime} (t)=t\mathbf{i}+e^{-t}\mathbf{j}- \dfrac{1}{t}\mathbf{k,}\;\mathbf\quad {r}(1)=\mathbf{i}-\mathbf{j}+2\mathbf{k}\)

Question

\(\mathbf{r}^{\prime} (t)=2\sin t\mathbf{i}+\cos t\mathbf{j}+\mathbf{k,}\;\mathbf\quad{r}(0)=\mathbf{i}-\mathbf{j}\)

Question

\(\mathbf{r}^{\prime} (t)=\cos ( 2t) \mathbf{i}+\sin ( 2t) \mathbf{j}+2\mathbf{k,}\;\mathbf\quad{r}(0)=\mathbf{i}+\mathbf{k}\)

Question

\(\mathbf{r}^{\prime} (t)=t^{-1}\mathbf{i}+t\mathbf{j}+t^{2} \mathbf{k,}\;\mathbf\quad{r}(1)=\mathbf{i}+\mathbf{j}+\mathbf{k}\)

Question

\(\mathbf{r}^{\prime} (t)=t^{3}\mathbf{i}+\dfrac{1}{t+1} \mathbf{j}+\mathbf{k,}\;\mathbf\quad{r}(0)=\mathbf{i}+\mathbf{j}+\mathbf{k}\)

Question

\(\mathbf{a}( t)\;=\;-32\mathbf{k,}\;\mathbf{v}(0)\;=\;\mathbf{0,}\;\mathbf{r}(0)\;=\;\mathbf{0}\)

Question

\(\mathbf{a}( t)\;=\;-32\mathbf{k,}\;\mathbf{v}(0)\;=\;\mathbf{i}+\mathbf{j,}\;\mathbf{r}(0)\;=\;\mathbf{0}\)

Question

\(\mathbf{a}( t)\;=\;\cos t\mathbf{i}+\sin t \mathbf{j,}\;\mathbf{v}(0)\;=\;\mathbf{i,}\;\mathbf{r}(0)\;=\;\mathbf{j}\)

Question

\(\mathbf{a}(t)\;=\;\cos t\mathbf{i}+\sin t\mathbf{j,}\;\mathbf{v}(0)\;=\;\mathbf{j,}\;\mathbf{r}(0)\;=\;\mathbf{i}\)

Question

\(\mathbf{a}( t)\;=\;-9.8\mathbf{k,}\;\mathbf{v}(0)=\mathbf{i,}\;\mathbf{r}(0)=5\mathbf{k}\)

800

Question

\(\mathbf{a}( t)\;=\;-9.8\mathbf{k,}\;\quad \mathbf{v}(0)=\mathbf{i}+\mathbf{j,}\;\mathbf{r}(0)=2\mathbf{i}\)

Question

\(\mathbf{a}( t)\;=\;e^{-t}\mathbf{i+j,}\;\quad \mathbf{v}(0)=\mathbf{i}+\mathbf{j,}\;\mathbf{r}(0)=\mathbf{i}-\mathbf{j}\)

Question

\(\mathbf{a}( t)\;=\;t^{2}\mathbf{i}-e^{-t}\mathbf{k,}\;\quad \mathbf{v}(0)=\mathbf{i-j,}\;\mathbf{r}(0)=\mathbf{k}\)

Question

Projectile Motion A projectile is fired at an angle of \(30 %TCIMACRO{\U{b0}} %BeginExpansion {{}^\circ} %EndExpansion \) to the horizontal with an initial speed of \(520\) m\(/\)s. What are its range, the time of flight, and the greatest height reached?

Question

Projectile Motion A projectile is fired with an initial speed of \(200\) m\(/\)s at an inclination of \(60 %TCIMACRO{\U{b0}} %BeginExpansion {{}^\circ} %EndExpansion \) to the horizontal. What are its range, the time of flight, and the greatest height reached?

Question

Projectile Motion A projectile is fired with an initial speed of \(100\) m\(/\)s at an inclination of \(\tan ^{-1}\left( \dfrac{5}{12}\right) \) to the horizontal.

1. Find parametric equations of the path of the projectile.
2. Find the range.
3. How long is the projectile in the air?
4. Graph the trajectory of the projectile.

Question

Projectile Motion A projectile is fired with an initial speed of \(120\) m\(/\)s at an inclination of \(\tan ^{-1}\left( \dfrac{3}{4 }\right) \) to the horizontal.

1. Find parametric equations of the path of the projectile.
2. Find the range.
3. How long is the projectile in the air?
4. Graph the trajectory of the projectile.

Question

Projectile Motion A projectile is fired up a hill that makes a \(30° %TCIMACRO{\U{b0}}% %BeginExpansion {{}^\circ}% %EndExpansion \) angle to the horizontal. Suppose the projectile is fired at an angle of inclination of \(45° %TCIMACRO{\U{b0}}% %BeginExpansion {{}^\circ}% %EndExpansion \) to the horizontal with an initial speed of \(100\textrm{ft}/\!\textrm{s}\). See the figure.

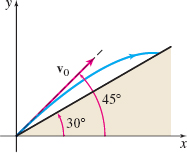
1. How far up the hill does the projectile land?
2. How long is the projectile in the air?

Question

Projectile Motion A projectile is propelled horizontally at a height of \(3\) m above the ground in order to hit a target 1 m high that is 30 m away. See the figure below. What should the initial velocity \({\bf v}_0\) of the projectile be?

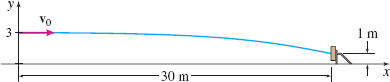
Question

A force whose magnitude is \(5\)N and whose direction is along the positive \(x\)-axis is continuously applied to a projectile of mass \(m=1 \)kg. At \(t=0{s}\), the position of the object is the origin and its velocity is \(3{m}/\!{s}\) in the direction of the positive \(y\)-axis.

1. Find the velocity and speed of the projectile after \(t\) seconds.
2. Find the position after the force has been applied for \(t\) seconds.
3. How long is the projectile in the air?
4. Describe the path of the projectile.

Question

An object of mass \(m\) is propelled from the point \((1,2)\) with initial velocity \(\mathbf{v}_{0}=3\mathbf{i}+4\mathbf{j}\). Thereafter, it is subjected only to the force \(\mathbf{F}=\dfrac{m}{\sqrt{2}}\left( - \mathbf{i}-\mathbf{j}\right) \). Find the vector equation for the position of the object at any time \(t>0\).

Question

Projectile Motion: Basketball In a Metro Conference basketball game on January 21, 1980, between Florida State University and Virginia Tech, a record was set. Les Henson, who is 6 ft 6 in. tall, made a basket from \(89\dfrac{1}{4}\) ft down court to win the game for Virginia Tech by a score of 79 to 77. Assuming he released the ball at a height of \(6\) ft \(6\) in. and threw it at an angle of \(45° %TCIMACRO{\U{b0}} %BeginExpansion {{}^\circ} %EndExpansion \) (to maximize distance), with what initial velocity was the ball tossed? See the figure. (Assume \(g=32{ft}/\!{s}^{2}\).)

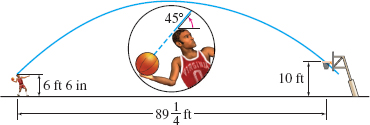
Question

Projectile Motion: Airplanes A plane is flying at an elevation of \(4.0\textrm{ km}\) with a constant horizontal speed of \(400\textrm{ km}/\!{h}\) toward a point directly above its target \(T\). See the figure. At what angle of sight \(\alpha \) should a package be released in order to strike the target? (Hint: \(g\approx 127{,}008{km}/\!{h}^{2}\).)

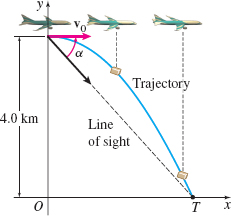
Question

Projectile Motion: Baseball A baseball is hit at an angle of \(45° %TCIMACRO{\U{b0}}% %BeginExpansion {{}^\circ}% %EndExpansion \) to the horizontal from an initial height of \(3\) ft. If the ball just clears the vines in front of the bleachers in Wrigley Field, which are \(10\) ft high and a distance of \(400\) ft from home plate, what was the initial speed of the ball? How long did it take the ball to reach the vines?

Question

Projectile Motion: Baseball An outfielder throws a baseball at an angle of \(45° %TCIMACRO{\U{b0}}% %BeginExpansion {{}^\circ}% %EndExpansion \) to the horizontal from an initial height of \(6\) ft. Suppose he can throw the ball with an initial velocity of \(100\) ft\(/\)s.

1. What is the furthest the outfielder can be from home plate to ensure that the ball reaches home plate on the fly?
2. How long is the ball in flight?
3. Use (a) and (b) to determine how fast a player must run to get from third base to home plate on a fly ball and beat the throw to score a run. (Hint: It is \(90 {ft}\) from third base to home plate.)

801

Question

Projectile Motion: Football In a field goal attempt on a flat field, a football is kicked at an angle of \(30° %TCIMACRO{\U{b0}}% %BeginExpansion {{}^\circ}% %EndExpansion $\) to the horizontal with an initial speed of \(65{ft}/\!{s}\).

1. What horizontal distance does the football travel while it is in the air?
2. To score a field goal, the ball must clear the cross bar of the goal post, which is \(10\) ft above the ground. What is the furthest from the goal post the kick can originate and score a field goal?

Question

Projectile Motion: Skeet Shooting A gun, lifted at an angle \( \theta _{0}\) to the horizontal, is aimed at an elevated target T, which is released the moment the gun is fired. See the figure. No matter what the initial speed \(v_{0}\) of the bullet is, show that it will always hit the falling target.

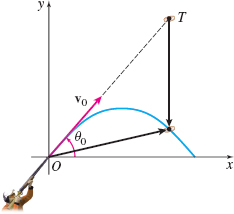
Question

1. Show that the maximum range of the projectile with position vector \(\mathbf{r}(t)=(v_{0}\cos \theta )t\mathbf{i} +\left[(v_{0}\sin \theta )t-\dfrac{1}{2}gt^{2}\right]\mathbf{j}\) occurs when \( \theta\;=\;\dfrac{\pi }{4}.\)
2. Show that the maximum range is \(\dfrac{v_{0}^{2}}{g}\).

Question

Show that the speed of the projectile whose position vector is given by \(\mathbf{r}( t)\;=\;(v_{0}\cos \theta )t\mathbf{i}+\left[ -\dfrac{1}{2}gt^{2}+(v_{0}\sin \theta )t\right] \mathbf{j}\) is least when the projectile is at its highest point.

Question

Show that a particle subject to no outside forces is either stationary or moves with constant speed along a straight line.

Question

Show that if \(\mathbf{r}^{\prime }(t)=\mathbf{0}\) for all \(t\) on some interval \(I\), then \(\mathbf{r}(t)=\mathbf{c}\), a constant vector, for all \(t\) in \(I\).

Question

Show that if \(\mathbf{f}^{\kern1pt\prime }(t)=\mathbf{g}^{\prime }(t)\) for all \(t\) in some interval \(I\), then \(\mathbf{f}(t)=\mathbf{g}(t)+\mathbf{c }\) for all \(t\) in \(I\).

Question

If \(\mathbf{c}\) is a constant vector and \(\mathbf{r=r} ( t) \) is continuous on a closed interval \([ a,b] \), show that \begin{equation*} \int_{a}^{b}[\mathbf{c}\,{\cdot}\, \mathbf{r}(t)]dt=\mathbf{c}\,{\cdot}\, \int_{a}^{b} \mathbf{r}(t)~dt \end{equation*}

Question

Use the result of Problem 44 to show that \begin{equation*} \left\Vert \int_{a}^{b}\mathbf{r}(t)dt\right\Vert \leq \int_{a}^{b}\left\Vert \mathbf{r}(t)\right\Vert dt \end{equation*}

[Hint: Set \(\mathbf{c}=\int_{a}^{b}\mathbf{r}(t)dt\) and find \( \left\Vert \mathbf{c}\right\Vert ^{2}\)].

Question

If \(\mathbf{c}\) is a constant vector and \(\mathbf{r}(t)\) is continuous on a closed interval \([a,~b]\), prove that \begin{equation*} \int_{a}^{b}[\mathbf{c}\times \mathbf{r}(t)]dt=\mathbf{c}\times \int_{a}^{b}\mathbf{r}(t)dt \end{equation*}