11.1 Vector Functions and Their Derivatives
758
OBJECTIVES
When you finish this section, you should be able to:
- Find the domain of a vector function (p. 758)
- Graph a vector function (p. 758)
- Find the limit and determine the continuity of a vector function (p. 761)
- Find the derivative of a vector function (p. 762)
- Find the derivative of a vector function using derivative formulas (p. 763)
A vector function is denoted by \(\mathbf{r}=\mathbf{r}(t)\), where \(t\) is a real number and \(\mathbf{r}\) is a vector. It is customary to use \(t\) as the independent variable, because in applications it often represents time.
spanDEFINITIONspan Vector Function
A vector-valued function of a real variable, or simply, a vector function, \(\mathbf{r}=\mathbf{r}(t)\), is a function whose domain is a subset of the set of real numbers and whose range is a set of vectors.
For a vector function \(\mathbf{r}=\mathbf{r}( t)\) in the plane whose domain is the closed interval \(a\leq t\leq b,\) the components of \(\mathbf{r}\) are two real functions \(x=x(t),\;y=y(t),\) each defined on the interval \(a\leq t\leq b.\) So, \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\mathbf{r}=\mathbf{r}(t)=\left\langle x( t), y( t) \right\rangle =x(t)\mathbf{i}+y(t)\mathbf{j}} \end{equation*}
For a vector function \(\mathbf{r}=\mathbf{r}( t)\) in space whose domain is the closed interval \(a\leq t\leq b\), the components of \(\mathbf{r}\) are three real functions \(x=x(t),\;y=y(t),\) and \(z=z(t)\), each defined on the interval \(a\leq t\leq b.\) So, \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\mathbf{r}=\mathbf{r}(t)= \langle x( t), y( t), z( t) \rangle =x(t)\mathbf{i}+y(t)\mathbf{j}+z(t)\mathbf{k}} \end{equation*}
NOTE
As with vectors and scalars, the symbol for a vector function is written using boldface roman type and the symbol for a real function is written using lightface italic type.
If no domain is specified for a vector function, it is assumed that the domain consists of all real numbers for which each of the component functions is defined.
1 Find the Domain of a Vector Function
Finding the Domain of a Vector Function
If \(\mathbf{r}(t) =\left(2t+2\right) \mathbf{i}+\sqrt{t}\mathbf{j}-\ln \left(t+3\right) \mathbf{k}\), then the components of \(\mathbf{r=r}(t)\) are \begin{equation*} {x(t) =2t+2\qquad y(t) =\sqrt{t}\qquad z(t) =- \ln \left( t+3\right)} \end{equation*}
Since no domain is specified, it is assumed that the domain consists of all real numbers \(t\) for which each of the component functions is defined. Since \(x=x(t)\) is defined for all real numbers, \(y=y(t)\) is defined for all real numbers \(t\geq 0,\) and \(z=z(t)\) is defined for all real numbers \(t\,{>}\!\,-\!3\), the domain of the vector function \(\mathbf{r=r}(t)\) is the intersection of these three sets, namely, the set of nonnegative real numbers, {\(t|t\geq 0\)}.
NOW WORK
Problem 17.
NEED TO REVIEW?
Parametric equations are discussed in Section 9.1, pp. 637-643.
2 Graph a Vector Function
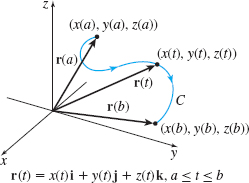
In general, the graph of a vector function \(\mathbf{r}\,{=}\,\mathbf{r}(t)\) with domain \(a\,{\leq}\,t\,{\leq}\,b\) is the curve \(C\) in the plane or in space traced out by the tip of the vector \(\mathbf{r}\,{=}\,\mathbf{r}(t)\) as \(t\) varies over the interval \(a\leq t\leq b.\) The components of the vector function are the parametric equations of the curve. We refer to the curve \(C,\) shown in Figure 1, traced out by the tip of \(\mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}\), \(a\leq t\leq b\), as a plane curve. The curve \(C,\) shown in Figure 2, traced out by the tip of \(\mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}+z(t)\mathbf{k}\), \(a\leq t\leq b\), is referred to as a space curve.
759

NOTE
From now on we will just say “the curve \(C\) is traced out by the vector function \(\mathbf{r}=\mathbf{r}(t)\)” rather than “traced out by the tip of the vector function.”
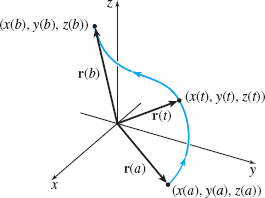
The curve \(C\) traced out by a vector function \(\mathbf{r}=\mathbf{r} (t)\), \(a\leq t\leq b\), has a direction, or an orientation. We show the orientation of \(C\) by placing arrows on its graph in the direction the vector \({\bf r} = {\bf r} (t)\) moves from \(t=a\) to \(t = b\). See Figure 3.
Graphing a Vector Function

Discuss the graph of the vector function \begin{equation*} \mathbf{r}(t)=\cos t\mathbf{i}+\sin t\mathbf{j}\qquad 0\leq t\leq 2\pi \end{equation*}
Solution The components of \(\mathbf{r}=\mathbf{r}(t)\) are the parametric equations \begin{equation*} x=x(t) =\cos t\qquad y=y(t) =\sin t\qquad 0\leq t\leq 2\pi \end{equation*}
Since \(x^{2}+y^{2}=\cos ^{2}t\,{+}\,\sin ^{2}t=1\), the vector function \(\mathbf{r=r}(t)\) traces out a circle with its center at the origin and radius \(1\). See Figure 4. The curve begins at \(\mathbf{r}( 0) =\cos 0\,\mathbf{i}\,{+}\,\sin 0\,\mathbf{j}=\mathbf{i},\) contains the vectors \(\mathbf{r} \!\left( \dfrac{\pi }{2}\right) =\cos \dfrac{\pi }{2}\,\mathbf{i}\,{+}\,\sin \dfrac{\pi }{2}\,\mathbf{j}=\mathbf{j},\) \(\mathbf{r}(\pi) =\cos \pi \mathbf{i}\,{+}\,\sin \pi \mathbf{j}=-\mathbf{i},\) and \(\mathbf{r}\!\left( \dfrac{3\pi }{2}\right) =-\mathbf{j}.\) It ends at \(\mathbf{r}( 2\pi )=\mathbf{i},\) so the positive direction of the circle is counterclockwise.
The domain of the vector function in Example 2 is restricted to \(0\leq t\leq 2\pi\). If \(t\) were unrestricted, the domain would be all real numbers. The graph would look the same, as would its orientation. The graph would just keep repeating over intervals of length \(2\pi .\)
NOW WORK
Problems 11 and 31.
NEED TO REVIEW?
Parametric equations and symmetric equations of a line are discussed in Section 10.6, pp. 734-736.
Graphing a Vector Function
Graph the curve \(C\) traced out by the vector function \begin{equation*} \mathbf{r}(t)=(2+3t)\mathbf{i}+(3-t)\mathbf{j}+2t\mathbf{k} \end{equation*}
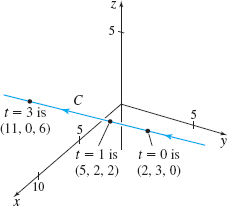
Solution The components of \(\mathbf{r=r}(t)\) are the parametric equations \begin{equation*} x(t)=2+3t\qquad y(t)=3-t\qquad z(t)=2t \end{equation*}
These are the parametric equations of a line in space containing the point \((2,3,0)\) (corresponding to \(t=0\)) and in the direction of the vector \(3\mathbf{i}-\mathbf{j}+2\mathbf{k}\). Solving for \(t\), we obtain the symmetric equations of this line \begin{equation*} \frac{x-2}{3}=\frac{y-3}{-1}=\frac{z}{2} \end{equation*}
Since \(\mathbf{r}(0)=2\mathbf{i}\,{+}\,3\mathbf{j}\) and \(\mathbf{r}(1)=5\mathbf{i}\,{+}\,2\mathbf{j}\,{+}\,2\mathbf{k}\), the positive direction of \(C\) is given by \(\mathbf{r}(1)-\mathbf{r}(0)=3\mathbf{i}-\mathbf{j}\,{+}\,2\mathbf{k}\). See Figure 5.
760
Graphing a Vector Function
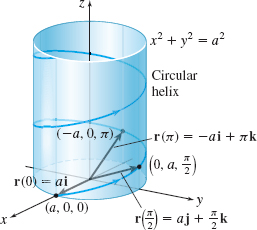
Graph the curve \(C\) traced out by the vector function \begin{equation*} r(t)=a\cos t\mathbf{i}+a\sin t\mathbf{j}+t\mathbf{k}\qquad t\geq 0 \end{equation*}
where \(a\) is a positive constant.
Solution The parametric equations of the curve \(C\) are \begin{equation*} x=x(t) =a\cos t\qquad y=y(t) =a\sin t\qquad z=z(t) =t \end{equation*}
Since \(x^{2}+y^{2}=a^{2}\cos ^{2}t+a^{2}\sin ^{2}t=a^{2},\) for any real number \(t\), any point \((x,y,z)\) on the curve \(C\) will lie on the right circular cylinder \(x^{2}+y^{2}=a^{2}\).
If \(t=0\), then \(\mathbf{r}( 0) =a\mathbf{i}\) so the point \((a,0,0)\) is on the curve. As \(t\) increases, the vector \(\mathbf{r}=\mathbf{r}(t)\) starts at \((a,0,0)\) and winds up and around the circular cylinder, one revolution for every increase of \(2\pi\) in \(t\). See Figure 6.
NEED TO REVIEW?
Cylinders are discussed in Section 10.7, pp. 748-750.
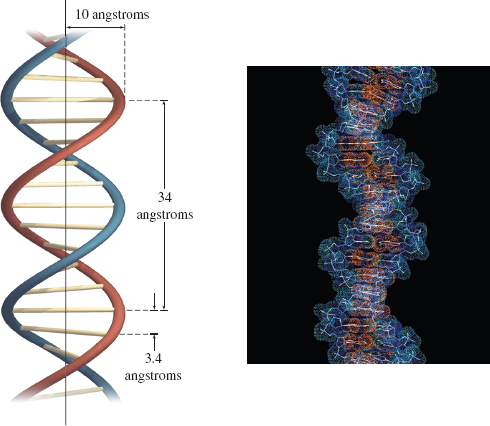
The space curve shown in Figure 6 is a circular helix and may be viewed as a coiled spring, much like a Slinky®. One of the many occurrences of a helix in nature is in the model of deoxyribonucleic acid (DNA), which consists of a double helix, that is, one helix intertwined with another helix, as shown in Figure 7.
NOW WORK
Problems 37 and 43.
3 Find the Limit and Determine the Continuity of a Vector Function
761
We use the components of a vector function to define limits, continuity, and the derivative of a vector function.
spanDEFINITIONspan Limit of a Vector Function
For a vector function \(\mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}\) in the plane \begin{equation*} \lim_{t\rightarrow t_{0}}\mathbf{r}(t)=\Big[ \lim_{t\rightarrow t_{0}}x(t) \Big] \mathbf{i}+\Big[ \lim_{t\rightarrow t_{0}}y(t)\Big] \mathbf{j} \end{equation*}
provided \(\lim\limits_{t\rightarrow t_{0}}x(t)\) and \(\lim\limits_{t\rightarrow t_{0}}y(t)\) both exist.
For a vector function \(\mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}+z(t)\mathbf{k}\) in space \begin{equation*} \lim_{t\rightarrow t_{0}}\mathbf{r}(t)=\Big[ \lim_{t\rightarrow t_{0}}x(t) \Big] \mathbf{i}+\Big[ \lim_{t\rightarrow t_{0}}y(t)\Big] \mathbf{j}+ \Big[ \lim_{t\rightarrow t_{0}}z(t)\Big] \mathbf{k} \end{equation*}
provided \(\lim\limits_{t\rightarrow t_{0}}x(t),\lim\limits_{t\rightarrow t_{0}}y(t)\), and \(\lim\limits_{t\rightarrow t_{0}}z(t)\) all exist.
For example, \begin{eqnarray*} \lim\limits_{t\rightarrow \pi /2}\left[ 2\cos t\mathbf{i}+2\sin ( 2t) \mathbf{j}+5\mathbf{k}\right] &=&\Big[ \lim\limits_{t\rightarrow \pi /2}( 2\cos t) \Big] \mathbf{i}+\Big[ \lim\limits_{t \rightarrow \pi /2}[ 2\sin ( 2t) ] \Big] \mathbf{j} +\Big[ \lim\limits_{t\rightarrow \pi /2}5\Big] \mathbf{k} \\[6pt] &=&\Big[ 2\lim\limits_{t\rightarrow \pi /2}\cos t\Big] \mathbf{i}+\Big[ 2\lim\limits_{t\rightarrow \pi /2}\sin ( 2t) \Big] \mathbf{j} +5\mathbf{k} \\[6pt] &=&2( 0) \mathbf{i}+2( 0) \mathbf{j}+5\mathbf{k}=5 \mathbf{k} \end{eqnarray*}
The definition of continuity of a vector function at a number is almost identical to the definition for real functions. To determine if a vector function is continuous at a real number, we consider the continuity of its components.
NEED TO REVIEW?
Continuity of a real-valued function is discussed in Section 1.3, pp. 93-100.
Continuity of a Vector Function at a Number
A vector function \(\mathbf{r}=\mathbf{r}(t)\) is continuous at a real number \(t_{0}\) if:
- \(\mathbf{r}(t_{0})\) is defined.
- \(\lim\limits_{t\rightarrow t_{0}}\mathbf{r}(t)\) exists.
- \(\lim\limits_{t\rightarrow t_{0}}\mathbf{r}(t)=\mathbf{r}(t_{0})\).
For example, the vector function \begin{equation*} \mathbf{r}(t)=t^{2}\mathbf{i}+(1+t)\mathbf{j}+\sin t\mathbf{k} \end{equation*}
is continuous at \(0\) because
- \(\mathbf{r}( 0) =0^{2}\mathbf{i}+( 1+0) \mathbf{j}+\sin 0\,\mathbf{k=j}\)
- \(\begin{align*} \lim\limits_{t\rightarrow 0}\mathbf{r}(t)=\lim\limits_{t\rightarrow 0}[t^{2}\mathbf{i}+(1+t)\mathbf{j}+\sin t\mathbf{k}]&=\Big[ \lim\limits_{t\rightarrow 0}t^{2}\Big] \mathbf{i}+\Big[ \lim\limits_{t\rightarrow 0}(1+t)\Big] \mathbf{j}+\Big[ \lim\limits_{t\rightarrow 0}\sin t\Big] \mathbf{k}\\ &=(0)\mathbf{i}+(1) \mathbf{j}+(0)\mathbf{k}=\mathbf{j} \end{align*}\)
- \(\lim\limits_{t\rightarrow 0}\mathbf{r}(t)=\mathbf{r}(0)=\mathbf{j}\)
That is, a vector function is continuous at a real number \(t_{0}\) if, and only if, each of its component functions is continuous at \(t_{0}\).
The definition of continuity on an interval for vector functions follows the pattern developed in Chapter 1 for real functions. That is, \(\mathbf{r}=\mathbf{r}(t)\) is continuous on an interval \(I\), provided each of its components is continuous on \(I\). For example, the vector function \(\mathbf{r}(t) =t^{2}\mathbf{i}+\left( 1+t\right) \mathbf{j}+\sin t\mathbf{k}\) is continuous for \(-\infty <t<\)\(\infty\) since \(x(t) =t^{2},\) \(y(t) =1+t,\) and \(z(t) =\sin t\) are continuous for all real numbers.
762
NOW WORK
Problem 49.
4 Find the Derivative of a Vector Function
The definition of a derivative for a vector function is very similar to the definition for a real function.
spanDEFINITIONspan Derivative of a Vector Function
The derivative of the vector function \(\mathbf{r=r}(t) \), denoted by \(\mathbf{r}^\prime(t) =\dfrac{d\mathbf{r}}{dt}\), is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\mathbf{r}^\prime (t)=\lim\limits_{h\rightarrow 0} \dfrac{\mathbf{r}(t+h)-\mathbf{r}(t)}{h}} \end{equation*}
provided the limit exists. If the limit exists, then we say \(\mathbf{r}\) is differentiable.
The next theorem provides a simple method for differentiating a vector function.
IN WORDS
To find the derivative of a vector function, differentiate each of its components.
THEOREM Differentiating a Vector Function
If \(\mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}\) and if \(x=x(t)\) and \(y=y(t)\) are both differentiable real functions, then \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\mathbf{r}^\prime (t) =x^\prime (t)\mathbf{ i}+y^\prime (t)\mathbf{j}} \end{equation*}
If \(\mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}+z(t)\mathbf{k}\) and if \(x=x(t),\) \(y=y(t)\), and \(z=z(t)\) are each differentiable real functions, then \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\mathbf{r}^\prime (t) =x^\prime (t)\mathbf{ i}+y^\prime (t)\mathbf{j}+z^\prime (t)\mathbf{k}} \end{equation*}
We prove this theorem for a vector function in space.
Proof
Use the definition of the derivative of a vector function. \begin{eqnarray*} \mathbf{r}^\prime (t)&=&\lim_{h\rightarrow 0}\frac{\mathbf{r}(t+h)-\mathbf{r} (t)}{h} \notag\\ &=&\lim_{h\rightarrow 0}\frac{[x(t+h)-x(t)]\;\mathbf{i}+[y(t+h)-y(t)] \;\mathbf{j}+[z(t+h)-z(t)]\;\mathbf{k}}{h} \notag \\ &=&\lim_{h\rightarrow 0}\left[ \frac{x(t+h)-x(t)}{h}\right]\!\;\mathbf{i} +\lim_{h\rightarrow 0}\left[ \frac{y(t+h)-y(t)}{h}\right]\!\;\mathbf{j} +\lim_{h\rightarrow 0}\left[ \frac{z(t+h)-z(t)}{h}\right]\!\;\mathbf{k} \notag \\ &=&x^\prime (t)\;\mathbf{i}+ {y}^\prime (t)\;\mathbf{j}+ {z}^\prime (t)\;\mathbf{k} \notag \end{eqnarray*}
In Leibniz notation, the derivative of a vector function \(\mathbf{r}\) has the form \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\dfrac{d\mathbf{r}}{dt}=\dfrac{dx}{dt}\mathbf{i}+ \dfrac{dy}{dt}\mathbf{j}\qquad \hbox{or} \qquad\dfrac{d\mathbf{r}}{dt}=\dfrac{ dx}{dt}\mathbf{i}+\dfrac{dy}{dt}\mathbf{j}+\dfrac{dz}{dt}\mathbf{k}} \end{equation*}
Finding the Derivative of a Vector Function
Find the derivative of each vector function.
(a) \(\mathbf{r}(t)=2\sin t\mathbf{i}+3\cos t\mathbf{j}\)
(b) \(\mathbf{r}(t)=e^{t}\mathbf{i}+(1+t)\mathbf{j}+\sin t\mathbf{k}\)
Solution
(a) We find the derivative of each component. Since \(\dfrac{d}{dt}\left( 2\sin t\right) =2\cos t\) and \(\dfrac{d}{dt}\left( 3\cos t\right) =-3\sin t,\) \begin{equation*} \dfrac{d\mathbf{r}}{dt}=\mathbf{r}^\prime (t)=2\cos t\mathbf{i}-3\sin t \mathbf{j} \end{equation*}
(b) \(\dfrac{d\mathbf{r}}{dt}=\mathbf{r}^\prime (t)=\dfrac{d}{dt} e^{t}\mathbf{i}+\dfrac{d}{dt}(1+t)\mathbf{j}+\dfrac{d}{dt}\sin t \mathbf{k}=e^{t}\mathbf{i}+\mathbf{j}+\cos t\mathbf{k}\)
763
Higher-Order Derivatives
Since the derivative \(\mathbf{r}^\prime\) is a vector function derived from the vector function \(\mathbf{r=r}(t)\), the derivative of \(\mathbf{r}^\prime\) (if it exists) is also a function, called the second derivative it of \(\mathbf{r}\), and denoted by \(\mathbf{r}^{\prime \prime}\). If the second derivative exists, then \(\mathbf{r}\) is called twice differentiable. Continuing in this fashion, we can find the third derivative \(\mathbf{r}^{\prime \prime \prime}\), the fourth derivative \(\mathbf{r}^{(4)},\) and so on, provided these derivatives exist. Collectively, these derivatives are called higher-order derivatives of the vector function \(\mathbf{r=r}(t) \mathbf{.}\)
Finding \(\mathbf{r}^{\prime}\) and \(\mathbf{r}^{\prime\prime}\) for a Vector Function
Find \(\mathbf{r}^{\prime} (t)\) and \(\mathbf{r}^{\prime \prime} (t)\) for the vector function \(\mathbf{r}(t)=e^{t}\mathbf{i}+\ln t\mathbf{j}-\cos t\mathbf{k}\).
Solution \begin{eqnarray*} \mathbf{r}^{\prime} (t) &=&\dfrac{d}{dt}e^{t}\mathbf{i}+\dfrac{d}{ dt}\ln t\mathbf{j}-\dfrac{d}{dt}\cos t\mathbf{k}=e^{t}\mathbf{i}+\frac{ 1}{t}\mathbf{j}+\sin t\mathbf{k} \notag \\[6pt] \mathbf{r}^{\prime \prime} (t) &=&\dfrac{d}{dt}e^{t}\mathbf{i}+ \dfrac{d}{dt}\frac{1}{t}\mathbf{j}+\dfrac{d}{dt}\sin t\mathbf{k}=e^{t} \mathbf{i}-\frac{1}{t^{2}}\mathbf{j}+\cos t\mathbf{k} \notag \end{eqnarray*}
NOW WORK
Problem 59.
5 Find the Derivative of a Vector Function Using Derivative Formulas
The derivative of a vector function \(\mathbf{r=r}(t)\) is defined in much the same way as the derivative of a real function \(y=f( x)\). For this reason, the sum and scalar multiplication formulas for vector functions are similar to the rules for real functions. However, for vector functions, there are formulas for the derivatives of the dot product and the cross product (in space). For vector functions, no formula analogous to the Quotient Rule exists.
THEOREM Derivative Formulas
If the vector functions \(\mathbf{u}=\mathbf{u}(t)\) and \(\mathbf{v}=\mathbf{v}(t)\) are differentiable and the real function \(y=f(t)\) is differentiable, then
- Sum formula: \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\dfrac{d}{dt}\left[ \mathbf{u}(t)+\mathbf{v}(t)\right] =\dfrac{\ d}{dt}\mathbf{u}(t)+\dfrac{d}{dt}\mathbf{v}(t)=\mathbf{u}^{\prime}(t)+\mathbf{ v}^{\prime} (t)} \end{equation*}
- Scalar multiplication formula: \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\dfrac{d}{dt}\left[ f(t)\mathbf{u}(t)\right] =\left[ \dfrac{d }{dt}f(t) \right] \mathbf{u}(t) +f(t) \left[ \dfrac{d}{dt}\mathbf{u}(t) \right] =f^{\prime} (t)\mathbf{u}(t)+f(t)\mathbf{u}^{\prime} (t)} \end{equation*}
- Dot product formula: \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\dfrac{d}{dt}\left[ \mathbf{u}(t) \,{\cdot}\, \mathbf{v} (t) \right] =\left[ \mathbf{u}(t)\,{\cdot}\, \mathbf{v}(t)\right] ^{\prime} =\mathbf{u}^{\prime}(t)\,{\cdot}\, \mathbf{v}(t)+\mathbf{u}(t)\,{\cdot}\, \mathbf{v} ^{\prime} (t)} \end{equation*}
- Cross product formula: \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\dfrac{d}{dt}\left[ \mathbf{u}(t) \times \mathbf{v} (t) \right] =\left[ \mathbf{u}(t)\times \mathbf{v}(t)\right] ^{\prime} =\mathbf{u}^{\prime}(t)\times \mathbf{v}(t)+\mathbf{u}(t)\times \mathbf{ v}^{\prime} (t)} \end{equation*}
where \(\mathbf{u}\) and \(\mathbf{v}\) are vector functions in space.
- Chain rule: \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\dfrac{d}{dt}\mathbf{v}\left( f(t) \right) = \mathbf{v}^{\prime}(f(t) )f^{\prime} (t)} \end{equation*}
764
The sum, scalar multiplication, and dot product formulas, and the Chain Rule hold for vector functions in the plane and in space. The cross product formula holds only for vectors in space. The proof for the scalar multiplication formula for a vector function in space is provided here. The proofs of the other four formulas are left as exercises. See Problems 99–102.
Proof (Scalar Multiplication Formula)
Let \(\mathbf{u}(t)=x(t)\kern1pt\mathbf{i}+y(t)\kern1pt\mathbf{j}+z(t)\;\mathbf{k}\). Then \begin{equation*} f(t)\mathbf{u}(t)=[ f(t)x(t)]\kern1pt\mathbf{i}+[ f(t)y(t)]\kern1pt\mathbf{j}+[ f(t)z(t)]\mathbf{k} \end{equation*}
We use the Product Rule and differentiate each component. \begin{eqnarray*} \left[ f(t)\mathbf{u}(t)\right] ^{\prime} &=&[f(t)x(t)]^{\prime} \mathbf{i} +[f(t)y(t)]^{\prime} \mathbf{j}+[f(t)z(t)]^{\prime} \mathbf{k} \notag \\[6pt] &=&[f(t)x^{\prime} (t)+f^{\prime} (t)x(t)]\kern1pt\mathbf{i}+[f(t)y^{\prime} (t)+f^{\prime} (t)y(t)]\kern1pt\mathbf{j}\\ &&+\,[f(t)z^{\prime} (t)+f^{\prime} (t)z(t)] \mathbf{k} \notag \\[6pt] &=&f^{\prime} (t)[x(t)\mathbf{i}+y(t)\mathbf{j}+z(t)\mathbf{k} ]+f(t)[x^{\prime} (t)\mathbf{i}+y^{\prime} (t)\mathbf{j}+z^{\prime} (t)\mathbf{k }] \notag \\[6pt] &=&f^{\prime} (t)\mathbf{u}(t)+f(t)\mathbf{u}^{\prime} (t) \notag \end{eqnarray*}
Notice that if \(f(t) =c\), where \(c\) is a constant, and \(\mathbf{u=u}(t)\) is a differentiable vector function, then \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\dfrac{d}{dt}\left[ c\mathbf{u}(t)\right] =c\left[ \dfrac{d}{dt}\mathbf{u}(t)\right] =c\mathbf{u}^{\prime}(t)} \end{equation*}

Finding the Derivative of a Cross Product
Find the derivative of \(\mathbf{u}(t)\times \mathbf{v}(t)\) if \[ \mathbf{u}(t)=\cos t\mathbf{i}+\sin t\mathbf{j}+t\mathbf{k}\qquad \hbox{and}\qquad \mathbf{v}(t)=t\mathbf{i}+\ln t\mathbf{j}+\mathbf{k} \]
Solution The derivatives of \(\mathbf{u}\) and \(\mathbf{v}\) are \[ \mathbf{u}^{\prime} (t)=-\!\sin t\mathbf{i}+\cos \dot{t}\mathbf{j}+\mathbf{k}\qquad \hbox{and}\qquad \mathbf{v}^{\prime}(t) =\mathbf{i}+\dfrac{1}{t} \mathbf{j} \]
We use the cross product formula. \begin{eqnarray*} \left[ \mathbf{u}(t)\times \mathbf{v}(t)\right] ^{\prime} &=&\mathbf{u}^{\prime} (t)\times \mathbf{v}(t)+\mathbf{u}(t)\times \mathbf{v}^{\prime} (t) \notag \\[6pt] &=&\left\vert \begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} &\mathbf{j} &\mathbf{k} \\ -\sin t &\cos t &1 \\ t &\ln t &1 \end{array} \right\vert +\left\vert \begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} &\mathbf{j} &\mathbf{k} \\ \cos t &\sin t &t \\ 1 &\dfrac{1}{t} &0 \end{array} \right\vert \notag \\[6pt] &=&\big[ ( \cos t-\ln t) \mathbf{i}+(\sin t+t)\mathbf{j} -[(\sin t)(\ln t)+t\cos t]\mathbf{k}\big] \\[6pt] &&+\left[ -\mathbf{i}+t\mathbf{ j}+\left( \frac{1}{t}\cos t-\sin t\right) \!\;\mathbf{k}\right] \notag \\[6pt] &=&(\cos t-\ln t-1)\mathbf{i}+(\sin t+2t)\mathbf{j}\\[6pt] &&+\left[ \frac{1}{t}\cos t-\sin t-(\sin t)(\ln t)-t\cos t\right] \!\;\mathbf{k} \notag \end{eqnarray*}
NOW WORK
Problems 73 and 79.
CAUTION
Be careful when using the cross product formula. Since a cross product is not commutative, order is important.
We can also find the derivative of \(\mathbf{u}\times \mathbf{v}\) in Example 7 by first finding the cross product of vector functions \(\mathbf{u}\) and \(\mathbf{v}\) and then differentiating. Try it, and compare the two solutions.