11.2 Assess Your UnderstandingPrinted Page 772
Concepts and Vocabulary
True or False If a vector function \(\mathbf{r}= \mathbf{r}(t)\) is differentiable at \(t_{0}\), \(\ a<t_{0}<b\), and \(P_{0}\) is the point on the curve traced out by \(\mathbf{r}=\mathbf{r}(t)\) corresponding to \(t=t_{0},\) then the tangent line to the curve at \(t_{0}\) contains the point \(P_{0}\) and has the direction \(\mathbf{r}( t_{0}) \mathbf{.}\)
False
True or False A curve traced out by a vector function \(\mathbf{r}=\mathbf{r}(t)\) is called a smooth curve on the interval \([ a,b]\) if \(\mathbf{r}=\mathbf{r}(t)\) is continuous on the interval \( [ a,b]. \)
False
True or False If \(C\) is a smooth curve traced out by a vector function \(\mathbf{r}=\mathbf{r}(t)\), \(a\leq t\leq b\), then \(\mathbf{T}(t)= \mathbf{r}^{\prime} (t)\) is the unit tangent vector to \(C\) at \(t.\)
False
True or False If \(C\) is a smooth curve traced out by a twice differentiable vector function \(\mathbf{r}=\mathbf{r}(t),\) \(a\leq t\leq b,\) and if \(\mathbf{T}\) is the unit tangent vector to \(C\), then \(\mathbf{N}( t) =\dfrac{\mathbf{T}( t) }{\left\Vert \mathbf{T}( t) \right\Vert }\) is the principal unit normal vector to \(C\) at \(t.\)
False
True or False For a smooth space curve \(C\) traced out by \(\mathbf{r}=\mathbf{r}(t),\) \(a\leq t\leq b,\) the integral \(\int_{a}^{b}\left\Vert \mathbf{r}^{\prime} ( t) \right\Vert dt\) equals the arc length along \(C\) from \(t=a\) to \(t=b.\)
True
True or False For a smooth curve traced out by a twice differentiable vector function, the unit tangent vector is orthogonal to the principal unit normal vector.
True
Skill Building
In Problems 7–14:
- (a) Find the tangent vector to each curve at t.
- (b) Graph the curve.
- (c) Add the graph of the tangent vector to (b).
\(\mathbf{r}(t)=t\mathbf{i}-t^{2}\mathbf{j,} \quad t=1\)
- (a) \(\mathbf{r}\,'(1) = \mathbf{i}-2\mathbf{j}\)
- (b) and
- (c)
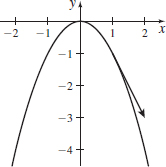
\(\mathbf{r}(t)=t\mathbf{i}-t^{3}\mathbf{j,} \quad t=-1\)
\(\mathbf{r}(t)=(t^{2}+1)\mathbf{i}+(1-t)\mathbf{j,} \quad t=1\)
- (a) \(\mathbf{r}\,'(1)=2\mathbf{i}-\mathbf{j}\)
- (b) and
- (c)
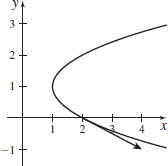
\(\mathbf{r}(t)=t^{3}\mathbf{i}+3t\mathbf{j,} \quad t=1\)
\(\mathbf{r}(t)=4t\mathbf{i}-\sqrt{t}\mathbf{j,} \quad t=1\)
- (a) \(r'(1) = 4{\rm {\bf i}} - \displaystyle{1 \over 2}{\rm {\bf j}}\)
- (b) and
- (c)
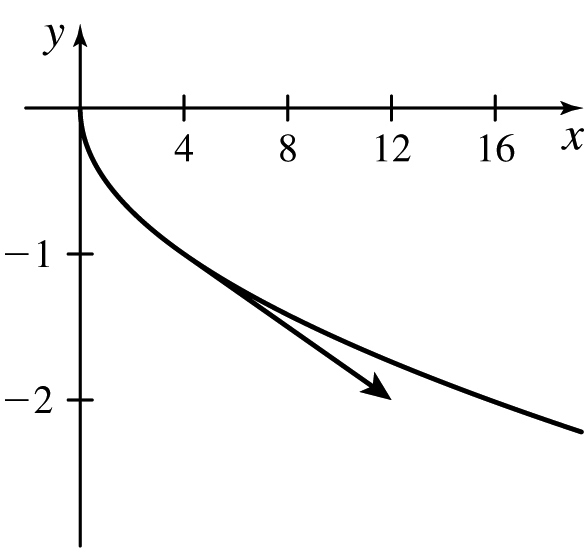
\(\mathbf{r}(t)=\sqrt{t}\mathbf{i}+\dfrac{1}{2}t\mathbf{j,} \quad t=4\)
\(\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j,} \quad t=0\)
- (a) \(\mathbf{r}\,'(0) = \mathbf{i}-\mathbf{j}\)
- (b) and
- (c)
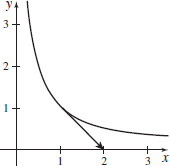
\(\mathbf{r}(t)=e^{2t}\mathbf{i}+e^{-t}\mathbf{j,} \quad t=0\)
In Problems 15–22, find the tangent vector to each curve at t.
\(\mathbf{r}(t)=(1-3t)\mathbf{i}+2t\mathbf{j}-(5+t)\mathbf{k,} \quad t=0\)
\(\mathbf{r}\,'(0) = -3\mathbf{i}+2 \mathbf{j} - \mathbf{k}\)
\(\mathbf{r}(t)=(2+t)\mathbf{i}+(2-t)\mathbf{j}+3t\mathbf{k,} \quad t=0\)
\(\mathbf{r}(t)=\cos ( 2t) \mathbf{i}+\sin (2t) \mathbf{j}-5\mathbf{k,} \quad t=\dfrac{\pi }{4}\)
\(\mathbf{r}\,'\left(\dfrac{\pi}{4}\right) = -2\mathbf{i} \)
\(\mathbf{r}(t)=3\mathbf{i}+\cos t\mathbf{j}+\sin t\mathbf{k,}\quad t=\dfrac{\pi }{6}\)
773
\(\mathbf{r}(t)=2\cos t\mathbf{i}+\mathbf{j}+2\sin t\mathbf{k,}\quad t=\dfrac{\pi }{6}\)
\(\mathbf{r}\,' \left(\dfrac{\pi}{6}\right)= -\mathbf{i} +\sqrt{3} \mathbf{k}\)
\(\mathbf{r}(t)=2\cos ( 2t) \mathbf{i}+2\sin ( 2t) \mathbf{j}+5\mathbf{k,} \quad t=\dfrac{\pi }{2}\)
\(\mathbf{r}(t)=e^{t}\cos t\mathbf{i}+e^{t}\sin t\mathbf{j}+e^{t}\mathbf{k,} \quad t=0\)
\(\mathbf{r}\,'(0) = \mathbf{i} + \mathbf{j} + \mathbf{k}\)
\(\mathbf{r}(t)=e^{-t}\cos t\mathbf{i}+e^{-t}\sin t\mathbf{j}-e^{-t}\mathbf{k,}\quad t=0 \)
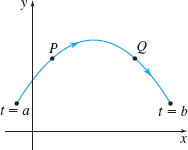
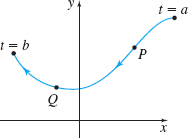
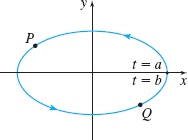
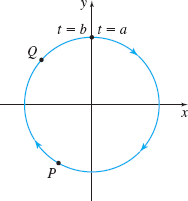
In Problems 23–26, draw the unit tangent vector \(\mathbf{T}\) and principal unit normal vector \(\mathbf{N}\) to \(C\) at the points \(P\) and \(Q.\) Be sure to use the orientation of the curve. Assume the length of a unit vector is one inch.
Figure below not drawn to scale.
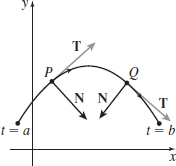
Figure below not drawn to scale.
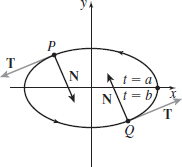
In Problems 27–42, for each vector function \(\mathbf{r}=\mathbf{r}( t), \) find the unit tangent vector \(\mathbf{T}\) and the principal unit normal vector \(\mathbf{N}\) at \(t\).
\(\mathbf{r}(t)=t\mathbf{i}+t^{2}\mathbf{j,} \quad t=1\)
\(\mathbf{T}(1) = \dfrac{\sqrt{5}}{5} \mathbf{i} + \dfrac{2\sqrt{5}}{5} \mathbf{j}\) and \(\mathbf{N}(1) = -\dfrac{2\sqrt{5}}{5} \mathbf{i}+\dfrac{\sqrt{5}}{5} \mathbf{j}\)
\(\mathbf{r}(t)=t\mathbf{i}-t^{3}\mathbf{j,} \quad t=-1\)
\(\mathbf{r}(t)=(t^{2}+1)\mathbf{i}+(1-t)\mathbf{j,} \quad t=1\)
\(\mathbf{T}(1) = \dfrac{2\sqrt{5}}{5} \mathbf{i} - \dfrac{\sqrt{5}}{5} \mathbf{j}\) and \(\mathbf{N}(1) = \dfrac{\sqrt{5}}{5} \mathbf{i} + \dfrac{2\sqrt{5}}{5} \mathbf{j}\)
\(\mathbf{r}(t)=t^{3}\mathbf{i}+3t\mathbf{j,} \quad t=1\)
\(\mathbf{r}(t)=\dfrac{2t}{t+1}\mathbf{i}-\dfrac{t^{2}}{t+1}\mathbf{j,} \quad t=1\)
\(\mathbf{T}(1) = \dfrac{2\sqrt{13}}{13} \mathbf{i} - \dfrac{3\sqrt{13}}{13} \mathbf{j}\) and \(\mathbf{N}(1) = -\dfrac{3\sqrt{13}}{13} \mathbf{i} - \dfrac{2\sqrt{13}}{13} \mathbf{j}\)
\(\mathbf{r}(t)=\sqrt{t}\mathbf{i}+\dfrac{1}{2}t\mathbf{j}, \quad t=4\)
\(\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j,} \quad t=0\)
\(\mathbf{T}(0) = \dfrac{\sqrt{2}}{2} \mathbf{i} - \dfrac{\sqrt{2}}{2} \mathbf{j}\) and \(\mathbf{N}(0) = \dfrac{\sqrt{2}}{2} \mathbf{i} + \dfrac{\sqrt{2}}{2} \mathbf{j}\)
\(\mathbf{r}(t)=e^{2t}\mathbf{i}+e^{-t}\mathbf{j,} \quad t=0\)
\(\mathbf{r}(t)=(1-3t)\mathbf{i}+2t\mathbf{j}-(5+t)\mathbf{k,} \quad t=0\)
\(\mathbf{T}(0) = -\dfrac{3\sqrt{14}}{14} \mathbf{i} + \dfrac{2\sqrt{14}}{14} \mathbf{j} - \dfrac{\sqrt{14}}{14} \mathbf{k}\) and \(\mathbf{N}(0) \) is undefined
\(\mathbf{r}(t)=(2+t)\mathbf{i}+(2-t)\mathbf{j}+3t\mathbf{k,} \quad t=0\)
\(\mathbf{r}(t)=2\cos t\mathbf{i}+\mathbf{j}+2\sin t\mathbf{k,}\quad t=\dfrac{\pi }{6}\)
\(\mathbf{T}\left(\dfrac{\pi}{6}\right) = -\dfrac12 \mathbf{i} + \dfrac{\sqrt{3}}2 \mathbf{k}\) and \(\mathbf{N}\left(\dfrac{\pi}{6}\right) = -\dfrac{\sqrt{3}}2 \mathbf{i} - \dfrac12 \mathbf{k}\)
\(\mathbf{r}(t)=3\mathbf{i}+\cos t\mathbf{j}+\sin t\mathbf{k,} \quad t=\dfrac{\pi }{6}\)
\(\mathbf{r}(t)=\cos ( 2t) \mathbf{i}+\sin (2t) \mathbf{j}-5\mathbf{k,} \quad t=\dfrac{\pi }{4}\)
\(\mathbf{T}\left(\dfrac{\pi}{4}\right) = -\mathbf{i}\) and \(\mathbf{N}\left(\dfrac{\pi}{4}\right) = -\mathbf{j}\)
\(\mathbf{r}(t)=2\cos ( 2t) \mathbf{i}+2\sin ( 2t) \mathbf{j}+5\mathbf{k,} \quad t=\dfrac{\pi }{2}\)
\(\mathbf{r}(t)=e^{t}\cos t\mathbf{i}+e^{t}\sin t\mathbf{j}+e^{t}\mathbf{k,}\quad t=0\)
\(\mathbf{T}(0) = \dfrac{\sqrt{3}}{3} \mathbf{i} + \dfrac{\sqrt{3}}{3} \mathbf{j} + \dfrac{\sqrt{3}}{3} \mathbf{k}\) and \({\rm {\bf N}}(0) = -\dfrac{\sqrt{2}}{2}{\rm {\bf i}} +\dfrac{\sqrt{2}}{2}{\rm {\bf j}}\)
\(\mathbf{r}(t)=e^{-t}\cos t\mathbf{i}+e^{-t}\sin t\mathbf{j}-e^{-t}\mathbf{k,} \quad t=0\)
In Problems 43–54, find the arc length \(s\) of each vector function.
\(\mathbf{r}(t)=t\mathbf{i}+(t^{3/2}+1)\mathbf{j}\) from \(t=1\) to \(t=8\)
\(s=\dfrac{1}{27} \left( 76^{3/2}-13^{3/2}\right)\)
\(\mathbf{r}(t)=t\mathbf{i}+t^{3/2}\mathbf{j}\) from \(t=0\) to \(t=4\)
\(\mathbf{r}(t)=8t\mathbf{i}+\dfrac{t^{6}+2}{t^{2}}\mathbf{j}\) from \(t=1\) to \(t=2\)
\( s= \dfrac{33}2\)
\(\mathbf{r}(t)=t\mathbf{i}+(1-t^{2/3})^{3/2}\mathbf{j}\) from \(t= \dfrac{1}{8}\) to \(t=1\)
\(\mathbf{r}(t)=t\mathbf{i}+2t\mathbf{j}+t\mathbf{k}\) from \(t=0\) to \(t=1\)
\(s = \sqrt{6}\)
\(\mathbf{r}(t)=2t\mathbf{i}+t\mathbf{j}+3t\mathbf{k}\) from \(t=1\) to \(t=3\)
\(\mathbf{r}(t)=\sin ( 2t) \mathbf{i}+\cos (2t) \mathbf{j}+t\mathbf{k}\) from \(t=0\) to \(t=\pi \)
\(s = \sqrt{5} \pi\)
\(\mathbf{r}(t)=\sin t\mathbf{i}+\cos t\mathbf{j}+bt\mathbf{k}\) from \(t=0\) to \(t=2\pi \)
\(\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j}+\sqrt{2}t\mathbf{k}\) from \(t=0\) to \(t=1\)
\(s = e - \dfrac1e\)
\(\mathbf{r}(t)=\cos ^{3}t\mathbf{i}+\sin ^{3}t\mathbf{j}+\mathbf{k}\) from \(t=0\) to \(t=\dfrac{\pi }{2}\)
\(\mathbf{r}(t)=e^{t}\cos t\mathbf{i}+e^{t}\sin t\mathbf{j}+e^{t}\mathbf{k}\) from \(t=\) \(0\) to \(t=2\pi \)
\(s = \sqrt{3} (e^{2\pi} - 1)\)
\(\mathbf{r}(t)=t^{2}\mathbf{i}-2\sqrt{2}\ t\mathbf{j}+(t^{2}-1)\mathbf{k}\) from \(t=0\) to \(t=1\)
![]() In Problems 55–58,
In Problems 55–58,
- (a) Graph the curve traced out by the vector function \(\mathbf{r=\mathbf{r}(t)}\).
- (b) Find the indicated arc length.
\(\mathbf{r}( t) =3\sin t\mathbf{i}-4\cos t\mathbf{j}\) from \(t=0\) to \(t=\pi\)
- (a)
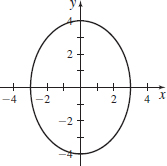
- (b) \(s \approx 11.052\)
\(\mathbf{r}( t) =5\cos t\mathbf{i}+3\sin t\mathbf{j}\) from \(t=0\) to \(t=\dfrac{\pi }{2}\)
\(\mathbf{r}( t) =2\sin t\mathbf{i}+4\cos (2t) \mathbf{j}\) from \(t=0\) to \(t= {2\pi}\)
- (a)
- (b) \(s \approx 33.637\)
\(\mathbf{r}( t) =4\sin ( 2t) \mathbf{i}-6\cos t\,\mathbf{j}\) from \(t=0\) to \(t=\dfrac{\pi }{2}\)
Applications and Extensions
Find all the points on the curve traced out by \(\mathbf{r} (t)=t^{2}\mathbf{i}+(t^{2}-1)\mathbf{j}-t\mathbf{k}\) at which \(\mathbf{r}(t)\) and its tangent vector are orthogonal.
\(\dfrac14\mathbf i - \dfrac34\mathbf j +\dfrac12 \mathbf k, - \mathbf j, \dfrac14\mathbf i - \dfrac34\mathbf j -\dfrac12 \mathbf k\)
Find the angle between the helix traced out by \(\mathbf{r}( t) =\cos t\mathbf{i}+t\mathbf{j}+\sin t\mathbf{k}\) and the \(y\)-axis.
The helix defined by \(\mathbf{r}(t)=3\sin t\mathbf{i}+3\cos t\mathbf{j}+4t\mathbf{k}\) and the direction \(\mathbf{k}\) meet at a constant angle. Find the angle to the nearest degree.
\(\theta \approx 37^\circ\)
The helix defined by \(\mathbf{r}(t)=2\cos t\mathbf{i}+2\sin t\mathbf{j}+t\mathbf{k}\) and the direction \(\mathbf{k}\) meet at a constant angle. Find the angle to the nearest degree.
In Problems 63–66, find the angle between the tangent vectors to the curves traced out by \(\mathbf{r}_{1}(t_{1})\) and \(\mathbf{r}_{2}(t_{2})\) at the point of intersection given.
\(\mathbf{r}_{1}(t_{1})=t_{1}\mathbf{i}+\sin \left( \pi t_{1}\right) \mathbf{j}+\mathbf{k}\) and \(\mathbf{r}_{2}(t_{2})=\mathbf{i}+t_{2}\mathbf{j}+\left( 1+t_{2}\right) \mathbf{k}\) at \(\left( 1,0,1\right)\)
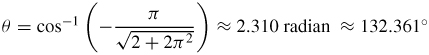
\(\mathbf{r}_{1}(t_{1})=\sin \left( 2t_{1}\right) \mathbf{i}+\sin t_{1}\mathbf{j}+t_{1}\mathbf{k}\) and \(\mathbf{r}_{2}(t_{2})=t_{2}^{2}\mathbf{i}+t_{2}\mathbf{j}+t_{2}^{3}\mathbf{k}\) at \(\left( 0,0,0\right) \)
\(\mathbf{r}_{1}(t_{1})=(e^{t_{1}}-1)\mathbf{i}-\cos \left( \pi t_{1}\right) \mathbf{j}+t_{1}\mathbf{k}\) and \(\mathbf{r}_{2}(t_{2})=(1-t_{2})\mathbf{i}-\mathbf{j}+(t_{2}-1)\mathbf{k}\) at \((0,-1,~0)\)
\(\theta = 90^\circ\)
774
\(\mathbf{r}_{1}(t_{1})=t_{1}^{2}\mathbf{i}-( t_{1}-3) \mathbf{j}-( t_{1}-3) \mathbf{k}\) and \(\mathbf{r}_{2}(t_{2})=\big(t_{2}^{2}+3\big)\mathbf{i}-(t_{2}-2) \mathbf{j}+t_{2}\mathbf{k}\) at \((4,1,1)\)
If \(\mathbf{r}=\mathbf{r}( t) \) is a vector function in space that is twice differentiable, then the cross product of the unit tangent vector and the principal unit normal vector, \(\mathbf{T}\times \mathbf{N}\), defines a third unit vector \(\mathbf{B}( t).\) This vector \(\mathbf{B}\), called the binormal vector, is orthogonal to both the unit tangent vector \(\mathbf{T}\) and the principal unit normal vector \(\mathbf{N}\), as shown in the figure.
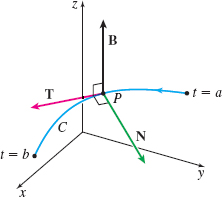
In Problems 67–70, find the unit tangent vector \(\mathbf{T}\), the principal unit normal vector \(\mathbf{N}\), and the binormal vector \(\mathbf{B}\) to each vector function.
\(\mathbf{r}(t)=t^{2}\mathbf{i}-( t-3) \mathbf{j}-( t-3) \mathbf{k}\)
\(\mathbf{T}(t) = \dfrac{2t}{\sqrt{4t^2+2}}\mathbf{i} - \dfrac{1}{\sqrt{4t^2+2}} \mathbf{j} - \dfrac{1}{\sqrt{4t^2+2}} \mathbf{k}\), \(\mathbf{N}(t) = \dfrac{1}{\sqrt{2t^2+1}} \mathbf{i} + \dfrac{t}{\sqrt{2t^2+1}}\mathbf{j} + \dfrac{t}{\sqrt{2t^2+1}}\mathbf{k}\), and \(\mathbf{B}(t) = -\dfrac{\sqrt{2}}{2} \mathbf{j} + \dfrac{\sqrt{2}}{2} \mathbf{k}\)
\(\mathbf{r}(t)=\left( t+5\right) \mathbf{i}-\left( t+5\right) \mathbf{j}+t^{2}\mathbf{k}\)
\(\mathbf{r}(t)=\cos t\mathbf{i}+\sin t\mathbf{j}+t\mathbf{k}\)
\(\mathbf{T}(t) = -\dfrac{\sqrt{2}}{2} \sin t \mathbf{i} + \dfrac{\sqrt{2}}{2} \cos t \mathbf{j} + \dfrac{\sqrt{2}}{2} \mathbf{k}\), \(\mathbf{N}(t) = -\cos t \mathbf{i} - \sin t \mathbf{j}\), and \(\mathbf{B}(t) = \dfrac{\sqrt{2}}{2} \sin t \mathbf{i} - \dfrac{\sqrt{2}}{2} \cos t \mathbf{j} + \dfrac{\sqrt{2}}{2} \mathbf{k}\)
\(\mathbf{r}(t)=2\sin t\mathbf{i}+2\cos t\mathbf{j}+3t\mathbf{k}\)
Suppose the vector function \(\mathbf{r=r}(t)\) in space is differentiable and has a nonzero tangent vector at \(t_{0}\). Find the direction cosines for the tangent vector at \(t_{0}\).
\(\cos \alpha = \dfrac{x'(t_0)}{\left\Vert\mathbf{r}\,'(t_0)\right\Vert}\), \(\cos \beta = \dfrac{y'(t_0)}{\left\Vert\mathbf{r}\,'(t_0)\right\Vert}\), \(\cos \gamma = \dfrac{z'(t_0)}{\left\Vert\mathbf{r}\,'(t_0)\right\Vert}\)
Show that at any point, the tangent vectors to a helix \(\mathbf{r}(t)=a\cos t\mathbf{i}+a\sin t\mathbf{j}+bt\mathbf{k}\), where \(a\) and \(b\) are real numbers, intersect the direction of the \(z\)-axis at a constant angle.
Challenge Problems
Use Simpson's Rule with \(n=4\) to approximate the length of the curve \(\mathbf{r}(t)=t^{2}\mathbf{i}+t^{3}\mathbf{j}+(2t+3)\mathbf{k}\), \(0\leq t\leq 2\).
\(s \approx 10.516\)
- (a) Approximate the arc length of \(\mathbf{r}( t) =3\sin t\mathbf{i}-4\cos t\mathbf{j}\) from \(t=0\) to \(t=\pi \) using Simpson's Rule with \(n=4.\)
- (b) Approximate the arc length of \(\mathbf{r}( t)=3\sin t\mathbf{i}-4\cos t\mathbf{j}\) from \(t=0\) to \(t=\pi \) using the Trapezoidal Rule with \(n=6.\)
- (c) Compare the answers to (a) and (b) to the result given by technology (see Problem 55).
- (a) Approximate the arc length of \(\mathbf{r}( t) =2\sin t\mathbf{i}+4\cos ( 2t)\mathbf{j}\) from \(t=0\) to \(t=2\pi\) using Simpson's Rule with \(n=4.\)
- (b) Approximate the arc length of \(\mathbf{r}( t) =2\sin t\mathbf{i}+4\cos ( 2t)\mathbf{j}\) from \(t=0\) to \(t=2\pi\) using the Trapezoidal Rule with \(n=6.\)
- (c) Compare the answers to (a) and (b) to the result given by technology (see Problem 57).
- (a) \(s = \dfrac{4\pi}3 \approx 4.189\)
- (b) \(s \approx 33.510\)
- (c) See the Student Solutions Manual
Approximate the length of the curve \(\mathbf{r}(t)=\dfrac{1}{3}t^{3}\mathbf{i}+(t-1)\mathbf{j}+2\mathbf{k}\), \(0\leq t\leq \dfrac{1}{2}\), correct to three decimal places, by expanding the integrand in a power series.