Question

Multiple Choice If a smooth curve \(C\) is traced out by the vector function \(\mathbf{r}=\mathbf{r}(t)\), \(a\leq t\leq b,\) then the parameter \(t\) is the arc length if and only if [(a) \(\left\Vert \mathbf{r}(t)\right\Vert\;=1\), (b) \(\left\Vert \mathbf{r}^{\prime}(t)\right\Vert\;=0\), (c) \(\left\Vert \mathbf{r}^{\prime\prime}(t)\right\Vert\;=1\), (d) \(\left\Vert \mathbf{r}^{\prime}(t)\right\Vert\;=1]\) for all \(t.\)

Question

True or False The curvature \(\kappa\) of a straight line equals the slope of the line.

Question

True or False The curvature \(\kappa\) of a circle equals the radius of the circle.

Question

True or False The curvature \(\kappa\) of a twice differentiable smooth curve \(C\) equals the magnitude of the rate of change of the unit tangent vector \(\mathbf{T}\) with respect to arc length.

Question

True or False The curvature \(\kappa\) of a twice differentiable smooth curve \(C\): \(\mathbf{r}=\mathbf{r}(t)\) is \(\kappa\;=\;\dfrac{\left\Vert \mathbf{r}^{\prime} (t) \times \mathbf{r} ^{\prime \prime} (t) \right\Vert }{\left\Vert \mathbf{r}(t) \right\Vert ^{3}}.\)

Question

The curvature of a twice differentiable function \(y=f(x)\) is \(\kappa\) = _______.

Question

The curvature of the circle \(x^{2}+\left( y-2\right) ^{2}=9\) is \(\kappa\) = _______.

Question

True or False The radius \(\rho\) of the osculating circle at a point \(P\) of a smooth curve \(C\) equals \(\kappa,\) provided \(\kappa \neq 0.\)

Question

\(\mathbf{r}(t)=4\cos t\mathbf{i}-4\sin t\mathbf{j},\quad 0\leq t\leq 2\pi\)

Question

\(\mathbf{r}(t)=\sin (3t)\mathbf{i}+\cos (3t)\mathbf{j,} \quad 0\leq t\leq 2\pi\)

Question

\(\mathbf{r}(t)=t^{2}\mathbf{i}+t\mathbf{j},\quad 0\leq t\leq 4\)

Question

\(\mathbf{r}(t)=t\mathbf{i}+t^{3}\mathbf{j,}\quad 0\leq t\leq 2\)

Question

\(\mathbf{r}(t)=(2t+1)\mathbf{i}+(3t-2)\mathbf{j},\quad 0\leq t\leq 5\)

Question

\(\mathbf{r}(t)=\mathbf{i}+t\mathbf{j},\quad 0\leq t\leq 1\)

Question

\(\mathbf{r}(t)=\left( \dfrac{2}{\sqrt{13}}t+1\right) \mathbf{i}+\left( \dfrac{3}{\sqrt{13}}t-2\right) \mathbf{j}\), \(0\leq t\leq 5\sqrt{13}\)

Question

\(\mathbf{r}(t)=\mathbf{i}+t^{2}\mathbf{j},\quad 0\leq t\leq 1\)

Question

\(\mathbf{r}(t)=\sin t\mathbf{i}+\cos t\mathbf{j}+t\mathbf{k}\)

Question

\(\mathbf{r}(t)=a\sin t\mathbf{i}+a\cos t\mathbf{j}+\sqrt{1-a^{2}}\kern1pt t\mathbf{k}\)

Question

Question

Question

\(\mathbf{r}(t)=t^{2}\mathbf{i}+\dfrac{2}{t}\mathbf{j}\)

Question

\(\mathbf{r}(t)=2t\mathbf{i}+t^{3}\mathbf{j}\)

Question

\(\mathbf{r}(t)=2\sin t \mathbf{i}+2\cos t\mathbf{j}\)

Question

\(\mathbf{r}(t)=\cos t\mathbf{i}+2\sin t\mathbf{j}\)

Question

\(\mathbf{r}(t)=(3t-t^{3})\mathbf{i}+3t^{2} \mathbf{j}\)

Question

\(\mathbf{r}(t)=(3t-t^{3})\mathbf{i}+(3t+t^{3})\mathbf{j}\)

Question

\(\mathbf{r}(t)=t\mathbf{i}+2t\mathbf{j}+t\mathbf{k}\)

Question

\(\mathbf{r}(t)=2t\mathbf{i}+t\mathbf{j}+3t\mathbf{k}\)

Question

\(\mathbf{r}(t)=\sin ( 2t) \mathbf{i}+\cos ( 2t) \mathbf{j}+t\mathbf{k}\)

Question

\(\mathbf{r}(t)=\sin t\mathbf{i}\,{+}\,\cos t\mathbf{j}\,{+}\,bt\mathbf{k}\)

Question

\(\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j}+\sqrt{2}t\mathbf{k}\)

Question

\(\mathbf{r}(t)=e^{t}\mathbf{i}+e^{2t}\mathbf{j}+e^{-t}\mathbf{k}\)

Question

\(\mathbf{r}(t)=\cos ^{3}t\mathbf{i}+\sin ^{3}t\mathbf{j}+\mathbf{k}\)

Question

\(\mathbf{r}(t)=4\cos ^{3}t\mathbf{i}+ 3\mathbf{j} + 4\sin^{3}t\mathbf{k}\)

Question

\(y=x^{2}\) at \((1,1)\)

Question

\(y=2x-x^{2}\) at \((1,1)\)

Question

\(y=x^{2}-x^{3}\) at \((1,0)\)

Question

\(y=x^{-3/2}\) at \((1,1)\)

Question

\(y=\sqrt{x}\) at \(\big(2,\sqrt{2}\big)\)

Question

\(y=\dfrac{1}{\sqrt{x}}\) at \((1,1)\)

Question

\(4x^{2}+9y^{2}=36\) at \((0,2)\)

Question

\(y=\sec x-1\) at \(\left(\! \dfrac{\pi}{4}, \sqrt{2}-1\!\right)\)

Question

\(y=e^{x}\) at \((0,1)\)

Question

\(y=\ln (x+1)\) at \(( 2,\ln 3)\)

Question

\(y=x^{3}-6x\) at \((1,-5)\)

Question

\(y=\dfrac{1}{x^{2}}\) at \((-1,1)\)

Question

\(y=\sin x\) at \(\left( \dfrac{\pi }{2},1\right)\)

Question

\(y=e^{-x}\) at \((0,1)\)

Question

\(x^{2}+xy+y^{2}=3\) at \((1,1)\)

Question

\(y^{2}-y+x=0\) at \((0,0)\)

Question

\(y=\ln ( \sec x)\) at \(\left(\dfrac{\pi }{4}, \ln \sqrt{2}\right)\)

Question

\(y=\cosh x\) at \((0,1)\)

Question

\(\mathbf{r}(t)=3t^{2}\mathbf{i}+(3t-t^{3})\mathbf{j,}\quad t=1\)

Question

\(\mathbf{r}(t)=t\mathbf{i}+t^{2}\mathbf{j}+t^{3}\mathbf{k},\quad t=1\)

Question

\(\mathbf{r}(t)=\sin t\mathbf{i}+\cos ( 2t) \mathbf{j},\quad t=\dfrac{\pi }{4}\)

Question

\(\mathbf{r}(t)=\sin t\mathbf{i}+\cos t\mathbf{j}+bt\mathbf{k,}\quad b>0,\quad t=\dfrac{\pi }{4}\)

Question

\(\mathbf{r}(t)=\sin ( 2t) \mathbf{i}+\cos ( 2t) \mathbf{j}+t\mathbf{k,}\quad t=\dfrac{\pi }{4}\)

Question

\(\mathbf{r}(t)=\cos ^{3}t\mathbf{i}+\sin ^{3}t\mathbf{j}+\mathbf{k,}\quad t=\dfrac{\pi }{3}\)

Question

\(\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j}+\sqrt{2}\kern1ptt\mathbf{k},\quad t=0\)

Question

\(\mathbf{r}(t)=a(3t-t^{3})\mathbf{i}+3at^{2}\mathbf{j}+a(3t+t^{3})\mathbf{k,}\quad a>0, \quad t=1\)

Question

\(\mathbf{r}(t)=4a\cos ^{3}t\mathbf{i}+4a\sin ^{3}t\mathbf{j}+3a\cos ( 2t) \mathbf{k,}\quad a>0,\quad t=\dfrac{\pi }{4}\)

Question

\(\mathbf{r}(t)=t\mathbf{i}+2t\mathbf{j}+\sqrt{1-5t^{2}}\kern1pt\mathbf{k},\quad -\dfrac{\sqrt{5}}{5} < t< \dfrac{\sqrt{5}}{5},\quad t=0\)

Question

Radius of Curvature Show that the radius of curvature of the parabola \(y=ax^{2}+bx+c\) is a minimum at its vertex.

Question

Radius of Curvature Show that the radii of curvature at the ends of the axes of the ellipse \(b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}\) are \(\dfrac{b^{2}}{a}\) and \(\dfrac{a^{2}}{b},\quad a>0, b>0.\)

Question

Maximum Curvature Find the point on the curve \(y=\ln x\) at which the curvature is maximum.

Question

Maximum Curvature Find the point on the curve \(y=e^{x}\) at which the curvature is maximum.

Question

Maximum Curvature Find the point(s) on the curve \(y=\dfrac{1}{3}x^{3}\) at which the curvature is maximum.

Question

Maximum Curvature Find the point(s) on the curve \(y=\sin x\) at which the curvature is maximum.

Question

Maximum Curvature Find \(\alpha >0\) so that \(\mathbf{r} (t)= \alpha \cos t\mathbf{i} + \alpha \sin t\mathbf{j}+t\mathbf{k}\) has maximum curvature.

Question

Curvature of a Plane Curve What is the curvature at a point of inflection of a plane curve?

Question

Curvature of a Catenary Show that the curvature of the catenary \(y=a\cosh \dfrac{x}{a}\), \(a>0\), at any point \((x,y)\) is \(\dfrac{a}{y^{2}}\).

Question

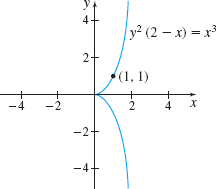
Curvature of a Cissoid Find the curvature of the cissoid \(y^{2}(2-x)=x^{3}\) at the point \((1,1)\). See the figure.

Question

Curvature of a Cycloid Find the curvature of the cycloid \(x( \theta)\;=\;\theta -\sin \theta\) and \(y( \theta )\;=\;1-\cos \theta\) at the highest point of an arch. See the figure.

Question

1. Find the curvature of the curve \(\mathbf{r} (t)=(1-t^{3})\mathbf{i}+t^{2}\mathbf{j}\).
2. Graph \(\mathbf{r}=\mathbf{r}(t)\). Where is the curvature undefined? Do you see any geometric reason for this?

Question

Curvature of a Spiral Find the curvature of the spiral \(\mathbf{r}(t)=e^{-t}\cos t\mathbf{i}+e^{-t}\sin t\mathbf{j}\) shown in the figure. How does the curvature behave when \(t\rightarrow \infty\)? Do you see any geometric reason for this?

784

Question

Curvature Find the curvature \(\kappa\) of the curve \(\mathbf{r}(t)=2a\cos t\mathbf{i}+2a\sin t\mathbf{j}+bt^{2}\mathbf{k},\qquad a>0, b>0.\)

Question

Curvature Show that the curvature of an ellipse \(\dfrac{x^{2}}{ a^{2}}+\dfrac{y^{2}}{b^{2}}=1,\) \(a> b,\) is a maximum at the points \( \left( \pm a,0\right)\) and is a minimum at the points \(\left( 0,\pm b\right).\)

Source: Contributed by the students at the University of Missouri.

Question

Curvature Show that the circular helix \(\mathbf{r}( t)\;=\;a\cos t\mathbf{i}+a\sin t\mathbf{j}+t\mathbf{k}\) has constant curvature.

Source: Contributed by the students at the University of Missouri.

Question

Write a vector equation for the curve \(C\) traced out by \( \mathbf{r}(t)=2t\mathbf{i}+(2t-1)\mathbf{j}+t\mathbf{k}\), \(0\leq t\leq 2\), using arc length \(s\) as the parameter. [Hint: For each \(t\), \(0\leq t\leq 2\), calculate the length \(s(t)\) of the curve from \(0\) to \(t\).]

Question

Compare the solutions of Problems 13 and 15. Then show how to change the parameter \(t\) of the line \(\mathbf{r}(t)=(at+b)\mathbf{i}+(ct+d) \mathbf{j}\), where either \(a\neq 0\) or \(c\neq 0\), to one that is arc length as measured along the line.

Question

Suppose a smooth curve \(C\) is traced out by a twice differentiable vector function \(\mathbf{r}=\mathbf{r}(t)\), \(a\leq t\leq b\). If the curvature \(\kappa \neq 0\) at a point \(P\) on \(C\), show that the position vector \(\mathbf{C}\) of the center of the osculating circle at \(P\) is given by \begin{equation*} \mathbf{C}(t)=\mathbf{r}(t)+\rho \mathbf{N}(t) \end{equation*} where \(\mathbf{N}\) is the principal unit normal vector to \(C\) at \(P\), and \(\rho\;=\;\dfrac{1}{\kappa }\).

Question

Use the result of Problem 81 to find the center and radius of the osculating circle for the helix \(\mathbf{r}(t)=a\sin t\mathbf{i}+a\cos t\mathbf{j}+a^{2}t\mathbf{k}\), \(a>0;\) \begin{equation*} {\bf (a)}\enspace at\enspace t=\dfrac{\pi }{2}.\qquad {\bf (b)}\enspace at\enspace t=\pi. \end{equation*}

Question

Show that the three vectors \(\mathbf{T}, \mathbf{N}\), and \(\mathbf{B}\) form a collection of mutually orthogonal unit vectors at each point on \(C\).

Question

Show that \(\dfrac{d\mathbf{T}}{ds}=\kappa (s)\mathbf{N}(s)\).

Question

Show that \(\dfrac{d\mathbf{B}}{ds}\) is orthogonal to both \(\mathbf{B}(s)\) and \(\mathbf{T}(s).\)

Question

If the torsion \(\tau (s)\) of \(C\) is defined by the equation \(\dfrac{d\mathbf{B}}{ds}=-\tau \mathbf{N}\), show that \(\dfrac{d\mathbf{N}}{ds}=\tau \mathbf{B}-\kappa \mathbf{T}\).

Question

Find \(\kappa, \mathbf{T}, \mathbf{N}\), and \(\mathbf{B}\) for \(\mathbf{r}(s)=\dfrac{1}{\sqrt{2}}\left[ \sin s\mathbf{i}+\cos s\mathbf{j}+s\mathbf{k}\right].\)

Question

Curvature of a Polar Curve Show that the formula for the curvature of a polar curve \(r=f(\theta )\) is \begin{eqnarray*} \\[-24pt] \kappa\;=\;\frac{\left\vert r^{2}+2\!\left( \dfrac{dr}{d\theta }\right) ^{2}-r\left( \dfrac{d^{2}r}{d\theta ^{2}}\right) \right\vert }{\left[ r^{2}+\left( \dfrac{dr}{d\theta }\right) ^{2}\right] ^{3/2}} \end{eqnarray*}

Question

\(r=2\cos ( 2\theta )\) at \(\theta\;=\;\dfrac{\pi }{12}\)

Question

\(r=e^{a\theta }\) at \(\theta\;=\;\dfrac{\pi }{2}, a>0\)

Question

\(r=a\theta\) at \(\theta\;=\;1\) and \(a>0\)

Question

\(r=1-\cos \theta\) at \(\theta\;=\;0\)

Question

\(r=3-2\sin \theta\) at \(\theta\;=\;\dfrac{\pi }{6}\)

Question

\(r=2+3\cos \theta\) at \(\theta\;=\;\dfrac{\pi }{3}\)

Question

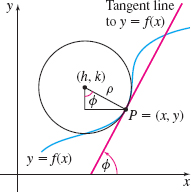
Use the figure below to show that the coordinates \((h,k)\) of the center of curvature of \(y=f(x)\) are \begin{equation*} h=x-\rho \sin \phi\qquad k=y+\rho \cos \phi \end{equation*} where \(\rho \) is the radius of curvature. Show that \begin{equation*} \sin \phi\;=\;\frac{y^{\prime} }{\sqrt{1+( y^{\prime} ) ^{2}}}\qquad \hbox{and}\qquad \cos \phi\;=\;\frac{1}{\sqrt{1+( y^{\prime} ) ^{2}}} \end{equation*} so \begin{equation*} h=x-\frac{y^{\prime} \left[ 1+( y^{\prime} ) ^{2}\right] }{y^{\prime \prime}}\qquad \hbox{and}\qquad k=y+\frac{1+( y^{\prime} ) ^{2}}{y^{\prime \prime} } \end{equation*}

Question

\(y=x^{2}\) at \(x=1\)

Question

\(y=\sin x\) at \(x=\dfrac{\pi }{2}\)

Question

\(y=\dfrac{x}{x+1}\) at \((0, 0)\)

Question

\(x^{3}+y^{3}=4xy\) at \((2, 2)\)

Question

\(xy=4\) at \(x=2\)

Question

As a point \(P\) moves along a curve \(C\), the center of curvature corresponding to \(P\) traces out a curve \(C_{1}\) called the evolute of \(C\); conversely, \(C\) is the involute of \(C_{1}\). Show that parametric equations of the evolute of \(y=\dfrac{1}{2}x^{2}\) are \(h=-x^{3}\), \(k=\dfrac{3}{2}x^{2}+1\). Then eliminate the parameter \(x\) to obtain \begin{equation*} h^{2}=\frac{8}{27}\left( k-1\right) ^{3} \end{equation*}

Question

Refer to Problem 101. Find parametric equations and a rectangular equation for the evolute of \(\mathbf{r}( t)\;=\;a\cos t\mathbf{i}+b\sin t\mathbf{j}\), \(a>0, b>0, 0\leq t\leq 2\pi \).