Question

True or False If a twice differentiable vector function \(\mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}+z(t)\mathbf{k}\) represents the position of a particle moving along a smooth curve, then the velocity vector is \(\mathbf{v}( t)\;=\;\mathbf{r}^{\prime} ( t) \) and the acceleration vector is \(\mathbf{a}( t)\;=\; \mathbf{r}^{\prime \prime} ( t) .\)

Question

True or False If a particle moving along a smooth curve traced out by a twice differentiable vector function \(\mathbf{r}= \mathbf{r}( t) \) travels at a constant speed, then the acceleration of the particle is directed along the unit tangent vector \(\mathbf{T}.\)

Question

True or False The acceleration vector \(\mathbf{a}= \mathbf{a}( t) \) of a particle moving along a smooth curve traced out by a twice differentiable vector function \(\mathbf{r}=\mathbf{r}( t)\) can be written as the sum of two orthogonal vectors: one vector in the direction of the velocity and the other vector perpendicular to the direction of the velocity.

Question

When the acceleration vector \(\mathbf{a}( t) \mathbf{ \ }\) of a particle moving along a smooth curve is written as \(\mathbf{a} (t)=v^{\prime} (t)\mathbf{T}(t)+\left[ v( t) \right] ^{2}\kappa \mathbf{N}(t),\) then \(a_{\mathbf{T}}=v^{\prime} ( t) \) is called the _____ component and \(a_{\mathbf{N}}=\left[ v( t) \right] ^{2}\kappa \) is called the _____ component of the acceleration vector \(\mathbf{a}\).

Question

\(\mathbf{r}(t)=t\mathbf{i}+t^{2}\mathbf{j}\)

Question

\(\mathbf{r}(t)=t\mathbf{i}-t^{3}\mathbf{j}\)

Question

\(\mathbf{r}(t)=(t^{2}+1)\mathbf{i}+(1-t)\mathbf{j}\)

Question

\(\mathbf{r}(t)=t^{3}\mathbf{i}+3t\mathbf{j}\)

Question

\(\mathbf{r}(t)= {4t}\mathbf{i}-{t^{3}}\mathbf{j}\)

Question

\(\mathbf{r}(t)=t^{3}\mathbf{i}+\dfrac{1}{2}t\mathbf{j}\)

Question

\(\mathbf{r}(t)=t^{2}\mathbf{i}+t\mathbf{j}-3t^{3}\mathbf{k}\)

Question

\(\mathbf{r}(t)=( t+1) \mathbf{i}+6t\mathbf{j}+t^{2}\mathbf{k}\)

Question

\(\mathbf{r}(t)=\sqrt{16-t^{2}}\kern.7pt\mathbf{i}+t^{2}\mathbf{j}+t\mathbf{k}\)

Question

\(\mathbf{r}(t)=\dfrac{1}{t^{2}}\mathbf{i}+\dfrac{t+1}{t^{2}}\mathbf{j}+t\mathbf{k}\)

Question

\(\mathbf{r}(t)=2\cos t\mathbf{i}+\sin t\mathbf{j}+t\mathbf{k}\)

Question

\(\mathbf{r}(t)=t\mathbf{i}+\sin({4}t)\mathbf{j}+cos({4}t)\mathbf{k}\)

Question

\(\mathbf{r}(t)=\sin t\mathbf{i}+\cos t\mathbf{j}+\sin (2t) \mathbf{k,}\quad t=\dfrac{\pi }{2}\)

Question

\(\mathbf{r}(t)=\sin t\mathbf{i}+\cos t\mathbf{j}+\sqrt{t}\mathbf{k,}\quad t=\pi \)

Question

\(\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j}\)

Question

\(\mathbf{r}(t)=e^{2t}\mathbf{i}+e^{-t}\mathbf{j}\)

Question

\(\mathbf{r}(t)=t\mathbf{i}+e^{t}\mathbf{j}\)

Question

\(\mathbf{r}(t)=t\mathbf{i}+\ln (1+t)\mathbf{j}\)

Question

\(\mathbf{r}(t)=3\sin ( 2t) \mathbf{i}+3\cos ( 2t) \mathbf{j}\)

Question

\(\mathbf{r}(t)=4\sin t\mathbf{i}-4\cos t\mathbf{j}\)

Question

\(\mathbf{r}(t)=2\cos t\mathbf{i}-3\sin t\mathbf{j}\)

Question

\(\mathbf{r}(t)=-\cos ( 3t) \mathbf{i}+2\sin ( 3t) \mathbf{j}\)

Question

\(\mathbf{r}(t)=2t\mathbf{i}+(t+1)\mathbf{j}\)

Question

\(\mathbf{r}(t)=(1-3t)\mathbf{i}+2t\mathbf{j}\)

Question

\(\mathbf{r}(t)=e^{t}\mathbf{i}+e^{2t}\mathbf{j}\)

Question

\(\mathbf{r}(t)=e^{-t}\mathbf{i}+e^{-2t}\mathbf{j}\)

Question

\(\mathbf{r}(t)=2\sin t\mathbf{i}+\cos t\mathbf{j}\)

Question

\(\mathbf{r}(t)=2\cos t\mathbf{i}+3\sin t\mathbf{j}\)

Question

\(\mathbf{r}(t)=(1-3t)\mathbf{i}+2t\mathbf{j}-(5+t)\mathbf{k}\)

Question

\(\mathbf{r}(t)=(2+t)\mathbf{i}+(2-t)\mathbf{j}+3t\mathbf{k}\)

Question

\(\mathbf{r}(t)=t\mathbf{i}+t^{2}\mathbf{j}+t^{3}\mathbf{k}\)

Question

\(\mathbf{r}(t)=\dfrac{t^{2}}{t+1}\mathbf{i}+\dfrac{1}{t+1}\mathbf{j}+\dfrac{t}{t+1}\mathbf{k}\)

Question

\(\mathbf{r}(t)=3\mathbf{i}+\cos t\mathbf{j}+\sin t\mathbf{k}\)

Question

\(\mathbf{r}(t)=t\mathbf{i}+\sin t\mathbf{j}+\cos t\mathbf{k}\)

Question

\(\mathbf{r}(t)=\ln t\mathbf{i}+\sqrt{t}\mathbf{j}+t^{3/2}\mathbf{k}\); \(t>0\)

Question

\(\mathbf{r}(t)=\cos ( 2t) \mathbf{i}+\sin ( 2t) \mathbf{j}-5\mathbf{k}\)

Question

\(\mathbf{r}(t)=e^{t}\cos t\mathbf{i}+e^{t}\sin t\mathbf{j}+e^{t}\mathbf{k}\)

Question

\(\mathbf{r}(t)=e^{-t}\cos t\mathbf{i}+e^{-t}\sin t\mathbf{j}-e^{-t}\mathbf{k}\)

Question

\(\mathbf{r}(t)=a\cos t\mathbf{i}+b\sin t\mathbf{j}+ct\mathbf{k}\) ;  \(a>0\), \(b>0\), \(c>0\)

Question

\(\mathbf{r}(t)=\cosh t\mathbf{i}+\sinh t\mathbf{j}+t\mathbf{k}\)

Question

Velocity and Acceleration Find the velocity and acceleration of a particle moving on the cycloid $$\mathbf{r}( t)\;=\;[ \pi t-\sin ( \pi t) ]\kern.7pt \mathbf{i}\,+ [ 1-\cos ( \pi t) ]\,\mathbf{j}\kern.7pt$$

Question

Velocity and Acceleration

1. Find the velocity and acceleration of a particle moving on the parabola \(\mathbf{r}( t) =( t^{2}-2t) \mathbf{i}+t\mathbf{j}\).
2. At what time \(t\) is the speed of the particle \(0?\)

Question

Acceleration A particle moves along the path \(y=3x^{2}-x^{3}\) with the horizontal component of the velocity equal to \(\dfrac{1}{3}\). Find the acceleration at the points where the velocity \(\mathbf{v}\) is horizontal. Graph the motion and indicate \(\mathbf{v}\) and \(\mathbf{a}\) at these points.

Question

Show that if the speed of a particle along a curve is constant, then the velocity and acceleration vectors are orthogonal.

Question

If a particle moves along the graph of \(y=f(x)\), show that \(a_{\mathbf{N}}=0\) at a point of inflection of the graph.

Question

Suppose that the vector function \(\mathbf{r}(t)=e^{t}\mathbf{i} +e^{-t}\mathbf{j}\) gives the position of a particle at time \(t\).

Question

A particle moves along the graph \(y=\dfrac{1}{2}x^{2}\) with constant speed \(v_{0}=2\). Find \(a_{\mathbf{T}}\) and \(a_{\mathbf{N}}\) in terms of \(x\) alone at a general point \(\left( x,\dfrac{1}{2}x^{2}\right) \) on the graph.

Question

If the motion of a particle is along the curve traced out by \( \mathbf{r}(t)=\alpha \cosh t\mathbf{i}+\beta \sinh t\mathbf{j}\), where \( \alpha >0\) and \(\beta >0\), show that the force acting on the particle is in the direction of \(\mathbf{r}=\) \(\mathbf{r}(t)\).

794

Question

Centripetal Force Refer to Example 5.

1. If the speed of the motorcycle is increased by 10%, by how much does the frictional force on the tires need to increase to keep the motorcycle moving along the same path?
2. If the radius of the circular track is halved, how much more slowly should the motorcycle be driven so the frictional force doesn’t change?

Question

Frictional Force A race car with mass \(1000\) kg is driven at a constant speed of \(200\) km/h around a circular track whose radius is \(75\) m. What frictional force must be exerted by the track on the tires to keep the car from skidding?

Question

Particle Collider The Large Hadron Collider (LHC), buried 100 m beneath Earth’s surface, is located near Geneva, Switzerland, and spans the border between France and Switzerland. The LHC is 26,659 m in circumference and, at full power, protons travel at a speed of \( 299{,}792{,}455.3\) m/s (99.9999991% the speed of light) around the circle. Find the magnitude of force necessary to keep a proton of mass \(m\) moving at this speed.

Source: http://public.web.cern.ch.

Question

Particle Collider At the Fermi National Accelerator Laboratory in Batavia, Illinois, protons were accelerated along a circular route with radius \(1\) km. Find the magnitude of the force necessary to give a proton of mass \(m\) a constant speed of \(280{,}000\) km/s.

Question

Magnitude of a Force Find the maximum magnitude of the force acting on a particle of mass \(m\) whose motion is along the curve \(\mathbf{r} (t)=4\cos t\mathbf{i}-2\cos ( 2t) \mathbf{j}\).

Question

Curvature of the Path of a Golf Ball A golf ball is hit with an initial speed \(v_{0}\) at an angle \(\theta \) to the horizontal and travels on a smooth curve traced out by the vector function \[ \mathbf{r}=\mathbf{r}(t)= ( v_{0}\cos \theta ) t\mathbf{i}+\left[ ( v_{0}\sin \theta ) t -\dfrac{1}{2}gt^{2}\right] \mathbf{j}, \]

where \(g=9.8{ m}/{ s}^{2}\) and \(0\leq \theta \leq \dfrac{\pi }{2}\).

1. At the highest point in the ball's trajectory, find the curvature of its path.
2. At the highest point in its trajectory, express the ball's acceleration vector using tangential and normal components. Are these components physically reasonable? Explain why.

Question

Velocity A particle moves on the circle \(x^{2}+y^{2}=1\) so that at time \(t\geq 0\) the position is given by the vector \begin{equation*} \mathbf{r}(t)=\frac{1-t^{2}}{1+t^{2}}\mathbf{i}+\frac{2t}{1+t^{2}}\mathbf{j} \end{equation*}

1. Find the velocity vector.
2. Is the particle ever at rest? Justify your answer.
3. Give the coordinates of the point that the particle approaches as \(t\) increases without bound.

Question

Velocity The position of a particle at time \(t\geq 0\) is given by \(\mathbf{r}( t)\;=\;e^{-t}\cos t\mathbf{i}+e^{-t}\sin t \mathbf{j}\).

1. Show that the path of the particle is part of the spiral \(r=e^{-\theta}\) (in polar coordinates).
2. Graph the path of the particle and indicate its direction of travel.
3. Show that the angle between the vector \(\mathbf{r}\) and velocity vector \(\mathbf{v}\) is always \(135{{}^\circ}\).

Question

Oscillating Motion Suppose a particle moves along the curve traced out by \(\mathbf{r}(t)=4\cos t\mathbf{i}-2\cos ( 2t) \mathbf{j}\).

1. Show that the particle oscillates on an arc of a parabola.
2. Graph the path.
3. Find the acceleration \(\mathbf{a}\) at points of zero velocity.

Question

If \(\mathbf{r}^{\prime} (t)=\mathbf{b}\times \mathbf{r}(t)\) for all \(t\), where \(\mathbf{b}\) is a constant vector, show that the acceleration \(\mathbf{a}(t)\) is perpendicular to \(\mathbf{b}\) and that the speed is constant.

Question

Mars Orbit NASA's Odyssey orbiter has a new mission to relay directly back to Earth the UHF telemetry taken by Curiosity, which landed on Mars on August 6, 2012. Odyssey is in a 'near-Mars' orbit at a height of \(400\textrm {km}\) above its surface. Find the speed of the Odyssey if the acceleration due to gravity on Mars is \(3.71\textrm{ m}/\textrm{s}^{2}\) and Mars' radius is \(3390\textrm{ km}\).

Question

Physics The power expended by a force \(\mathbf{F}(t)\) acting on an object of mass \(m\) with velocity \(\mathbf{v}(t)\) is the dot product \[ \hbox{Power}=\mathbf{F}(t)\,{\cdot}\, \mathbf{v}(t) \] The kinetic energy of an object of mass \(m\) and velocity \(\mathbf{v}(t)\) equals one-half the product of its mass times the square of its speed: \[ \hbox{Kinetic energy}=\frac{1}{2}m\left\Vert \mathbf{v}(t)\right\Vert ^{2} \] Show that the power of an object equals the rate of change of its kinetic energy with respect to time.

Question

Momentum In classical mechanics, the momentum \(\mathbf{p}(t)\) of an object of mass \(m\) at time \(t\) is defined as \(\mathbf{p}(t)=m\mathbf{v}(t)\), where \(\mathbf{v}(t)\) is the velocity of the object at time \(t\). Show that force equals the rate of change of momentum with respect to time.

Question

Angular Momentum The torque \({\tau }\) (Greek letter tau) produced by a force \(\mathbf{F}(t)\) acting on an object whose position at time \(t\) is \(\mathbf{r}(t)\) is defined as \({\tau }(t)=\mathbf{r}(t)\times \mathbf{F}(t)\). Torque measures the twist imparted on the object by the force. See the figure below. The angular momentum \(\mathbf{L}\) of an object of mass \(m\) and velocity \(\mathbf{v}(t)\) whose position at time \(t\) is \(\mathbf{r}(t)\) is \(\mathbf{L}(t)=\mathbf{r} (t)\times m\mathbf{v}(t)\). Show that the rate of change of angular momentum with respect to time equals the torque.

795

Question

Central Fields of Force A central field of force \(\mathbf{F}(t)\) is one whose direction is parallel to that of the position \(\mathbf{r}=\mathbf{r}(t)\) of the object it acts upon; that is, \(\mathbf{F}(t)=u(t)\mathbf{r}(t)\), where \(u(t)\) is a scalar function. Show that a central field of force produces zero torque.

Question

Hydrogen Atom  The Bohr model of an atom views it as a miniature solar system, with negative electrons in circular orbits around the positive nucleus. A hydrogen atom consists of a single electron in orbit around a single proton. The electric force \(F_{\rm {elec}}\) that the proton of charge \(e=1.60\times 10^{-19}\textrm {C}\) exerts on the electron, also of charge \(e=1.60\times 10^{-19}\textrm {C}\), is \(F_{\rm {elec}}=\dfrac{ke^{2}}{ r^{2}}\), where \(r\) is the distance in meters between the nucleus and the electron and \(k=9.0\times 10^{9}\textrm {N}\,{\cdot} \textrm {m}^{2}\!/\textrm {C}\) is a constant. Apply Newton's Second Law of Motion to the electron in a hydrogen atom and show that its speed is \(v=\sqrt{\dfrac{ke^{2}}{mr}}\), where \( m=9.11\times 10^{-31}\textrm {kg}\) is the mass of the electron.

Question

Analyzing Forces Use the formula \begin{equation*} \mathbf{F}=m\mathbf{a}=m\frac{dv}{dt}\mathbf{T}+mv^{2}\kappa\mathbf{N} \end{equation*} to discuss the forces on a passenger in a car.

1. What force corresponds to the push against the seat experienced by the passenger when the accelerator is depressed?
2. What force corresponds to the push against the door experienced by the passenger when the car is going around a curve?
3. How does this second force vary with the curvature of the road?
4. How does it vary with the speed of the car?

Question

Analyzing Motion Suppose \(\mathbf{r}=\mathbf{r}(t)\) gives the position of a particle at time \(t\). If the normal component of acceleration equals \(0\) at any time \(t\), explain why the motion of the particle must be in a straight line.

Question

Suppose the position of a particle in space is given by the vector function \(\mathbf{r}=\mathbf{r}( t) \). Show that if \( \mathbf{r}=\mathbf{r}( t) \) lies on a sphere, then the tangent vector is always orthogonal to \(\mathbf{r}=\mathbf{r}( t) \mathbf{ }\).

Question

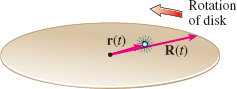
Coriolis Acceleration A particle moves on a disk from the center directly toward the edge. See the figure. The disk has radius 1 and is revolving in the counterclockwise direction at a constant angular speed \(\omega \), so the position of a point on the edge of the disk is given by \(\mathbf{R}(t)=\cos ( \omega t) \mathbf{i}+\sin ( \omega t) \mathbf{j}\). Suppose the position of the particle at time \(t\) is \( \mathbf{r}( t)\;=\;t\mathbf{R}( t) \).

(a) Show that the velocity \(\mathbf{v}\) of the particle is \begin{equation*} \mathbf{v}=\cos ( \omega t) \mathbf{i}+\sin ( \omega t) \mathbf{j}+t\mathbf{v}_{\mathbf{d}} \end{equation*}

where \(\mathbf{v}_{\mathbf{d}}=\mathbf{R}^{\prime} (t)\) is the velocity of the rotating disk.

(b) Also show that the acceleration \(\mathbf{a}\) of the particle is \begin{equation*} \mathbf{a}=2\mathbf{v}_{\mathbf{d}}+t\mathbf{a}_{\mathbf{d}} \end{equation*}

where \(\mathbf{a}_{\mathbf{d}}=\mathbf{R}^{\prime \prime} (t)\) is the acceleration of the rotating disk. The extra term \(2\mathbf{v}_{\mathbf{d}}\) is called the Coriolis acceleration, which results from the interaction of the rotation of the disk and the motion of the particle on the disk.

Question

Coriolis Acceleration Refer to Problem 72.

(a) Find the velocity and acceleration of a particle revolving on a rotating disk according to \begin{equation*} \mathbf{r}(t)=t^{2}\cos ( \omega t) \mathbf{i}+t^{2}\sin ( \omega t) \mathbf{j} \end{equation*}

(b) What is the Coriolis acceleration?

Question

Suppose a curve \(C\) is traced out by the vector function \(\mathbf{r}=\mathbf{r}(t)\). Find two nonparallel vectors that are orthogonal to \(\mathbf{T}(t)\) other than the principal unit normal vector. Assume \(\mathbf{T}(t)\neq \mathbf{0}\) and \(\mathbf{N}(t)\neq \mathbf{0}\).

Question

Let \(\mathbf{u}_{r}=\cos \theta \mathbf{i}+\sin \theta \mathbf{j}\) and \(\mathbf{u}_{\theta }=-\!\sin \theta \mathbf{i}+\cos \theta \mathbf{j}\).

1. Show that \(\mathbf{u}_{r}\) and \(\mathbf{u}_{\theta }\) are unit orthogonal vectors.
2. Show that \(\dfrac{d\mathbf{u}_{r}}{d\theta }=\mathbf{u}_{\theta }\) and \(\dfrac{d\mathbf{u}_{\theta }}{d\theta }=-\mathbf{u}_{r}\).
3. Suppose that \(\mathbf{r}(t)\) is the position vector of a plane curve and that the tip of \(\mathbf{r}(t)\) has polar coordinates \((r(t),~\theta (t)) \). Show that \(\mathbf{r}(t)=\;\left\Vert \mathbf{r}(t)\right\Vert \mathbf{u}_{r}=r(t) \mathbf{u}_{r}(t)\).
4. Use the Chain Rule to show that \begin{equation*} \mathbf{v}(t)=\frac{dr}{dt}\mathbf{u}_{r}+r\frac{d\theta }{dt}\mathbf{u} _{\theta }=r^{\prime} \mathbf{u}_{r}+r\theta ^{\prime} \mathbf{u}_{\theta } \end{equation*}
5. Show that \(\mathbf{a}(t)=[ r^{\prime \prime} -r( \theta ^{\prime}) ^{2}]\kern.7pt \mathbf{u}_{r}+[ r\theta ^{\prime \prime} +2r^{\prime}\theta ^{\prime} ]\kern.7pt \mathbf{u}_{\theta }\).

Question

Express the velocity \(\mathbf{v}\) and acceleration \(\mathbf{a}\) in terms of \(\mathbf{u}_{r}\) and \(\mathbf{u}_{\theta }\) for a motion along the polar curve \(r=2+\cos t\), where \(\theta\;=\;2t\).

Question

Find polar coordinate equations for \(\mathbf{r}(t)=e^{2t}\cos t\mathbf{i}+e^{2t}\sin t\mathbf{j}\) and express the velocity \(\mathbf{v}\) and acceleration \(\mathbf{a}\) in terms of \(\mathbf{u}_{r}\) and \(\mathbf{u}_{\theta }\).

Question

1. Show that if \(\mathbf{r^{\prime} }(t)\,{\cdot}\, \mathbf{r}(t)=0\) for all \(t\), then the motion \(\mathbf{r}(t)\) is on the surface of a sphere centered at the origin.
2. What can be said about a motion for which \(\mathbf{r}^{\prime \prime} (t)\,{\cdot}\, \mathbf{r}^{\prime} (t)=0\) for all \(t\)?
3. What can be said about a motion for which \(\mathbf{r}^{\prime} (t)\times \mathbf{r}(t)=0\) for all \(t\)?