12.1 Assess Your Understanding
Concepts and Vocabulary
Question
For the function \(z=f(x,y)=\sqrt{16-x^{2}-y^{2}}\), \(f( 2,3) =\) ___________.
Question
True or False The domain of a function of two variables is a nonempty set of points \((x,y) \) in the \(xy\)-plane.
Question
For a function \(w=f(x,y,z) \), the independent variable(s) is(are) _________ and the dependent variable(s) is(are) _________.
Question
True or False A level curve of the graph of \(z=f(x,y) \) is the set of points in the \(xy\)-plane for which \(f(x,y) =c\).
Skill Building
In Problems 5–10, evaluate each function.
Question
\(f(x, y)=3x+2y+xy\)
- \(f(0,1)\)
- \(f(2,1)\)
- \(f(x+\Delta x, y)\)
- \(f(x, y+\Delta y)\)
Question
\(f(x, y)=x^{2}y+x+1\)
- \(f(0,1)\)
- \(f(2,1)\)
- \(f(x+\Delta x, y)\)
- \(f(x, y+\Delta y)\)
Question
\(f(x, y)=\sqrt{xy}+x\)
- \(f(0,1)\)
- \(f(a^{2},t^{2});\quad a>0, t>0\)
- \(f(x+\Delta x, y)\)
- \(f(x, y+\Delta y)\)
Question
\(f(x, y)=e^{x+y}\)
- \(f(1,-1)\)
- \(f(x+\Delta x, y)\)
- \(f(x, y+\Delta y)\)
Question
\(F(x, y, z)=\dfrac{3xy+z}{x^{2}+y^{2}+z^{2}}\)
- \(F(0,0,1)\)
- \(F(0,1,0)\)
- \(F(\sin t,\cos t,0)\)
Question
\(F(x, y, z)=\dfrac{xyz}{x^{2}+y^{2}+z^{2}}\)
- \(F(1,-1,1)\)
- \(F(a,a,a)\), \(a\neq 0\)
- \(F(\sin t,\cos t,a)\)
Question
\(f(x, y)=3xy-x^{2},\) where \(x=x(t)=\sqrt{t}\) and \(y=y(t)=t^{2}.\) Find:
- \(f(x(0), y(0))\)
- \(f(x(1), y(1))\)
- \(f(x(4), y(4))\)
Question
\(f(x, y)=x^{2}+xy+y^{2},\) where \(x=x(t)=t\) and \(y=y(t)=t^{2}. \) Find:
- \(f(x(0), y(0))\)
- \(f(x(1), y(1))\)
- \(f(x(2), y(2))\)
816
In Problems 13–24 , find the domain of each function and graph the domain. Use a solid curve to indicate that the domain includes the boundary and a dashed curve to indicate that the domain excludes the boundary.
Question
\(f(x, y)=\dfrac{\sqrt{x}}{\sqrt{y}}\)
Question
\(f(x, y)=\sqrt{x}\sqrt{y}\)
Question
\(f(x, y)=\sqrt{xy}\)
Question
\(f(x, y)=\dfrac{xy}{x^{2}+y^{2}}\)
Question
\(f(x, y)=e^{x}\sin y\)
Question
\(f(x, y)=\dfrac{\ln x}{\ln y}\)
Question
\(f(x, y)=\sqrt{\dfrac{x^{2}+y^{2}}{x^{2}-y^{2}}}\)
Question
\(f(x, y)=\sqrt{\dfrac{x^{2}+y^{2}}{xy}}\)
Question
\(f(x, y)=\dfrac{5}{\sqrt{2y+x^{2}}}\)
Question
\(f(x, y)=\ln (x^{2}-y^{2})\)
Question
\(f(x, y)=\dfrac{y}{\sqrt{9-x^{2}-y^{2}}}\)
Question
\(f(x, y)=\tan ^{-1}(x^{2}+y^{2})\)
In Problems 25–28, find the domain of each function.
Question
\(f(x, y, z)=\dfrac{x^{2}+y^{2}}{z^{2}}\)
Question
\(f(x, y, z)=e^{z}\ln (x^{2}+y^{2})\)
Question
\(f(x, y, z)=\dfrac{z\sin x}{\cos y}\)
Question
\(f(x, y, z)=\dfrac{xyz}{\sqrt{x^{2}+y^{2}+z^{2}}}\)
In Problems 29–38, graph each surface.
Question
\(z=f(x,y)=3-x-y\)
Question
\(z=f(x,y)=2+x-y\)
Question
\(z=f(x,y)=x^{2}+y^{2}\)
Question
\(z=f(x,y)=x^{2}-y^{2}\)
Question
\(z=f(x,y)=\sqrt{4-x^{2}-y^{2}}\)
Question
\(z=f(x,y)=\sqrt{x^{2}+y^{2}-4}\)
Question
\(z=f(x,y)=\sin y\)
Question
\(z=f(x,y)=\cos x\)
Question
\(z=f(x,y)=4-x^{2}-y^{2}\)
Question
\(z=f(x,y)=x^{2}+y^{2}-4\)
In Problems 39–46, for each function
- Graph the level curves corresponding to the given values of c.
 Use a CAS to graph the surface.
Use a CAS to graph the surface.
Question
\(z=f(x, y)=x^{2}-y^{2}\) at \(c=0, 1, 4, 9\)
Question
\(z=f(x, y)=2x^{2}+y^{2}\) at \(c=0, 1, 4, 9\)
Question
\(z=f(x, y)=\sqrt{9-x^{2}-y^{2}}\) at \(c=0, 1, 3\)
Question
\(z=f(x, y)=\sqrt{x^{2}+y^{2}-4}\) at \(c=0, 1, 4, 9\)
Question
\(z=f(x, y)=x^{2}-2y\) at \(c=-4,-1,0,1,4\)
Question
\(z=f(x, y)=y^{2}-x\) at \(c=-4,-1,\,0, 1, 4\)
Question
\(z=f(x, y)=x+\sin y\) at \(c=0, 2, 4, 8\)
Question
\(z=f(x, y)=y-\ln x\) at \(c=1, 2, 4\)
In Problems 47–52:
- Describe in words the level surfaces of each function \(f\).
 Graph a level surface.
Graph a level surface.
- Does the graph match your verbal description?
Question
\(w=f(x,y,z)=x^{2}+z^{2}\)
Question
\(w=f(x,y,z)=x^{2}+y^{2}\)
Question
\(w=f(x,y,z)=z-2x-2y\)
Question
\(w=f(x,y,z)=x+y-z\)
Question
\(w=f(x,y,z)=4-x^{2}-y^{2}\)
Question
\(w=f(x,y,z)=z\)
Applications and Extensions
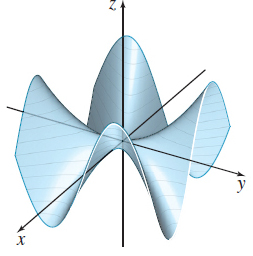
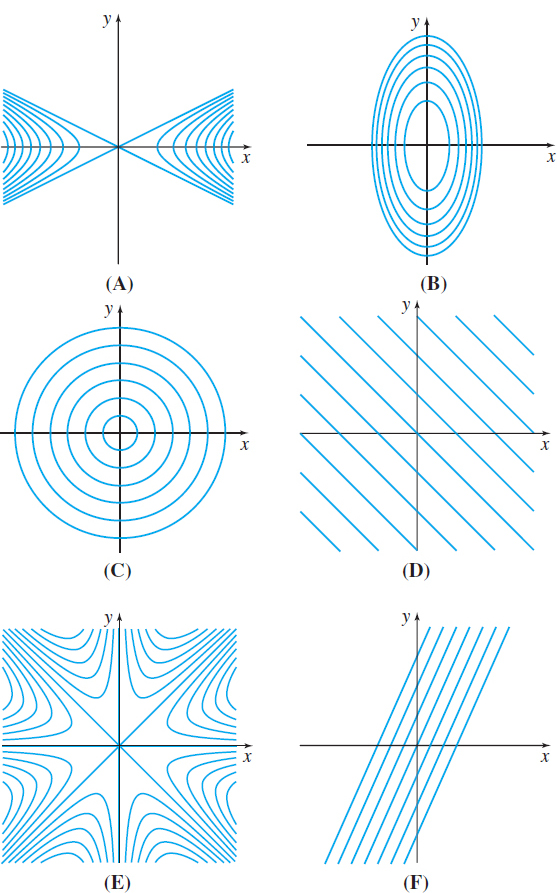
In Problems 53–58, match each surface to its corresponding level curves shown in (A)–(F).
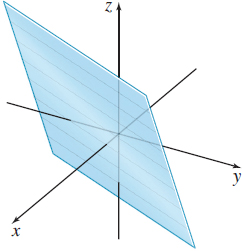
Question
\(z=f(x,y) =2x-y-2\)
Question
\(z=f(x,y) =x+y-3\)
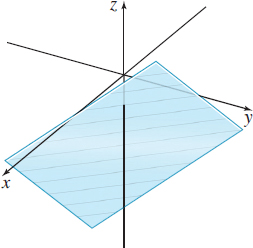
Question
\(z=f(x,y) =4x^{2}+y^{2}\)
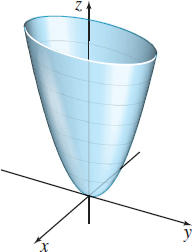
Question
\(z=f(x,y) =\sqrt{\dfrac{x^{2}}{4^{2}}+\dfrac{y^{2}}{4^{2}}}\)
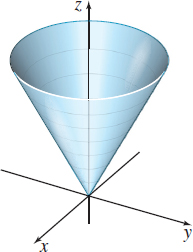
Question
\(z=f(x,y) =\dfrac{x^{2}}{2^{2}}-\dfrac{y^{2}}{1^{2}}\)

Question
\(z=f(x,y) =\dfrac{xy( x^{2}-y^{2}) }{x^{2}+y^{2}}\)
817
Question
Weather Maps A contour map of the temperatures in \(^\circ\)F of the western United States made on a given day in December 2011 is shown. The level curves are called isotherms.
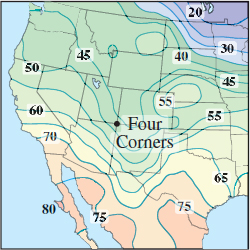
- Estimate the temperature at the Four Corners, the point where Utah, Colorado, Arizona, and New Mexico meet.
- Describe the change in temperature as you move south from the Four Corners.
- Describe the direction you would travel if you were at the Four Corners and wanted to move as quickly as possible to the next warmer temperature zone. Comment on how your path intersects the isotherm.
- A weather front is moving in if the isotherms are close together. Do you think a front is approaching the Four Corners? From what direction? Explain.
Question
Climbing a Mountain A topographical map of Mount Washington in New Hampshire is shown. Suppose a climber is at the base of the mountain and wants to climb to the summit. If she can begin at point \(A,\) \(B,\) \(C,\) or \(D,\) and climb straight up the mountain,
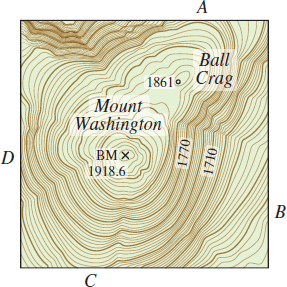
- At which point should she start to climb so the distance climbed is a minimum?
- At which point is the climb initially the steepest?
- Suppose someone is on any level curve of the mountain. Describe how he would walk so that no change in altitude occurs.
- Comment on how the paths in (a)–(c) intersect the contour lines.
Question
Social Science In psychology, the intelligence quotient (IQ) is measured by \(IQ = f(M,C) = 100\dfrac{M}{C}\), where \(M\) is a person’s mental age and \(C\) is the person’s chronological or actual age, \(0<C\leq 16.\)
- Find the IQ of a 12-year-old child whose mental age is 10.
- Find the IQ of a 10-year-old child whose mental age is 12.
- If a 10-year-old girl has an IQ of 139, what is her mental age? Round answers to the nearest integer.
Question
Mobile Data Cost One version of the AT&T DataConnect Pass plan for tablets has a monthly cost (in dollars) of \(C(x,y,z) = 35.00+0.1x+ 0.015y+0.0195z\), where \(x\) is the number of megabytes (mb) used domestically in excess of 200, \(y\) is the number of kilobytes (kb) of data sent to or received from Canada, and \(z\) is the number of kilobytes of data used outside the United States and Canada. Find the total monthly bill (in dollars) for 210 mb domestic, 250 kb Canadian, and 15 kb international usage.
(Source: AT&T Wireless.)
Question
Baseball A pitcher’s earned run average is calculated using the function \(A( N,I) =9\left( \dfrac{N}{I}\right) \), where \(N\) is the total number of earned runs given up in \(I\) innings pitched. Find:
- \(A( 3,4) \)
- \(A( 6,3) \)
- \(A( 2,9) \)
- \(A( 3,18) \)
Question
Field Goal Percentages in the NBA In the National Basketball Association (NBA), the adjusted field goal percentage is modeled by the function \(f(x,y,s) =\dfrac{x+1.5y}{s}\), where \(x\) is the number of two-point field goals made, \(y\) is the number of three-point field goals made, and \(s\) is the total of all field goals attempted.
- During the 2013 season, DeAndre Jordan of the Los Angeles Clippers led the league in field goal shooting. He made 234 out of 488 two-point attempts and no three-point attempts. Find his adjusted field goal percentage.
- During the 2013 season, Gordon Hayward of the Utah Jazz led the league in three-point shooting. He made 234 out of 527 two-point attempts and 234 out of 246 three-point attempts. Find his adjusted field goal percentage.
Question
Meteorology The apparent temperature (in degrees Fahrenheit) is measured by the heat index \(H\) according to the formula \[ \begin{eqnarray*} H &=&H( t,r)=-42.379+2.04901523\,t\\ &&+\,10.1333127\,r-0.22475541\,tr-0.00683783\,t^{2} \\ &&-\,0.05481717\,r^{2}+0.00122874\,t^{2}r+0.00085282\,tr^{2}\\ &&-\,0.00000199\,t^{2}r^{2} \end{eqnarray*} \]
where \(H=\) the heat index, \(t=\) the air temperature, and \(r=\) the percent relative humidity (for example, \(r=75\) when the relative humidity is \(75\%\)).
- What is the heat index when the air temperature is \(95^\circ\) and the relative humidity is \(50\%?\)
- If the air temperature is \(97^\circ\), what is the lowest relative humidity that will result in a heat index of 105\(^\circ\)?
818
Source: Weather Information Center; 4WX.com.
Question
Economics The production function for a toy manufacturer is given by the equation \(Q(L,M) =400L^{0.3}M^{0.7},\) where \(Q\) is the output in units, \(L\) is the labor in hours, and \(M\) is the number of machine hours. Find:
- \(Q( 19,21) \)
- \(Q(21,20) \)
Question
Rectangular Box Write the equation for the surface area \(S\) of an open box as a function of its length \(x\), width \(y\), and depth \(z\).
Question
Cost Function The cost C of the bottom and top of a cylindrical tank is $300 per square meter and the cost of the sides is $500 per square meter. Find a function that models the total cost of constructing such a tank as a function of the radius \(R\) and height \(h\), both in meters.
Question
Cost Function Find a function that models the total cost C of constructing an open rectangular box if the cost per square centimeter of the material to be used for the bottom is $4, for two of the opposite sides is $3, and for the remaining pair of opposite sides is $2.
Question
Cost Function Repeat Problem 69 for a closed rectangular box that has a top made of material costing $5 per square centimeter.
Question
Electrical Potential The formula \[ V(x, y)=\frac{9}{\sqrt{4-(x^{2}+y^{2})}} \]
gives the electrical potential \(V\) (in volts) at a point \((x,y)\) in the \(xy\) -plane. Draw the equipotential curves (level curves) for \(V=18\), 9, and 6 volts. Describe the surface \(z=V(x, y)\).
Question
Temperature The temperature \(T \)in degrees Celsius at any point \((x,y)\) of a flat plate in the \(xy\)-plane, is \(T=60-2x^{2}-3y^{2}\). Draw the isothermal curves (level curves) for \(T=60^\circ\)C, 54\(^\circ\)C, 48\(^\circ\)C, 6\(^\circ\)C, 0\(^\circ\)C. Describe the surface \(z=T(x, y)\).
Question
Electric Field The strength \(E\) of an electric field at a point \((x,y,z)\) resulting from an infinitely long charged wire lying along the \(x\)-axis is \[ E(x,y,z)=\frac{3}{\sqrt{y^{2}+z^{2}}} \]
Describe the level surfaces of \(E\).
Question
Gravitation The magnitude \(F\) of the force of attraction between two objects, one located at the origin and the other at the point \( (x, y, z)\neq (0,0,0)\), of masses \(m\) and \(M\) is given by \[ \begin{equation*} F=\frac{GmM}{x^{2}+y^{2}+z^{2}} \end{equation*} \]
where \(G=6.67\times 10^{-11}\rm{N}\rm{m}^{2}\!/\rm{\!kg}^{2}\) is the gravitational constant. Describe the level surfaces of \(F\).
Question
Thermodynamics The Ideal Gas Law, \(PV=nRT\), is used to describe the relationship among the pressure \(P\), volume \(V,\) and temperature \(T\) of an ideal gas, where \(n\) is the number of moles of gas and \(R\) is the universal gas constant. Describe the level curves for each of the following thermodynamic processes on an ideal gas:
- An isothermal process, that is, a process in which the temperature \(T\) is held constant
- An isobaric process, that is, a process in which the pressure \(P\) is held constant
- An isochoric process, that is, a process in which the volume \(V\) is held constant
Question
Electrostatics The electrostatic potential \(V\) (in volts) from a point charge \(Q\) at the origin is given by \[ V=\dfrac{\it kQ}{\sqrt{x^{2}+y^{2}+z^{2}}} \]
where \(k\) is a constant.
- Describe the level surfaces of \(V\). In electronics these are called the equipotential surfaces.
- What happens as the potential \(V\) gets close to 0?
Question
Magnetism The magnitude of the magnetic field \(B\) produced by a very long wire carrying a current \(I\) along the \(z\)-axis is given by \(B= \dfrac{\mu _{0}\,I}{2\pi \sqrt{x^{2}+y^{2}}}\), where \(\mu _{0}\) is a constant.
- Describe the level surfaces for \(B\).
(Hint: Notice that the field is independent of \(z\).) - What happens as the magnitude of \(B\) increases?
Question
Orbit of a Satellite The gravitational potential energy \(U\) of a satellite in orbit around Earth is \(U=-\dfrac{GM_{{\rm Earth}}m_{{\rm satellite}}}{\sqrt{x^{2}+y^{2}+z^{2}}}\), where the origin is placed at the center of Earth and \(G\) is the universal gravitation constant.
- Describe the level surfaces for \(U\).
- What happens as the gravitational potential energy gets close to 0?
Question
![]()
- Graph the surface \(z=f(x,y) =5e^{-( x^{2}+y^{2}) }.\)
- Experiment by changing the perspectives and plotting options until a clear picture of the graph is obtained.
- Change the style of the graph to show contour lines.
- Plot the level curves \(f(x,y) =c\quad c=1,2,3,4\).
- Explain how the curves obtained in (d) relate to the graph from (a).
Question
- Find the curve of intersection of the surfaces \(x^{2}+y^{2}+z^{2}=4\) and \(z=\dfrac{1}{3}(x^{2}+y^{2})\) above the \(xy\)-plane.
 Graph the surfaces from (a).
Graph the surfaces from (a).- Does the graph support the result from (a)?
Question
Level Curves On the same set of axes, graph the level curves of \(f(x, y)=x^{2}-y^{2}\) and \(g(x, y)=xy\). Use \(c=\pm 1, \pm 2, \pm 3\) for both \(f\) and \(g\).
Question
Orthogonal Curves Show that at each point \(P_{0}\neq (0,0)\), the level curve of \(f(x,y)=x^{2}-y^{2}\) through \(P_{0}\) is perpendicular to the level curve of \(g(x, y)=xy\) through \(P_{0}\). The two families of level curves are said to be orthogonal.
Challenge Problem
Question
Describe the set of points \((x,y,z)\) satisfying the conditions \(x^{2}+y^{2}+z^{2}<1\) and \(x^{2}+y^{2}<z^{2},\) where \(z>0\).
