Question

True or False  To find the partial derivative \(f_{y}(x,y) ,\) differentiate \(f\) with respect to \(x\) while treating \(y\) as if it were a constant.

Question

Multiple Choice  The partial derivative \(f_{x}(x_{0},y_{0})\) equals the slope of the tangent line to the curve of intersection of the surface \(z=f(x,y)\) and the plane [(a) \(x=x_{0},\) (b) \(y=y_{0},\) (c) \(z=z_{0},\) (d) \(x+y+z=0\)] at the point \((x_{0},y_{0},f(x_{0},y_{0}) )\) on the surface.

Question

True or False  \(f_{x}(x,y)\) equals the rate of change of \(f\) in the direction of the positive \(x\)-axis.

Question

The two second-order partial derivatives \(\dfrac{\partial ^{2}z}{\partial x\partial y}\) and \(\dfrac{\partial ^{2}z}{\partial y\partial x}\) are called ____ partials.

Question

True or False  If \(f(x,y)=x\;\cos\;y,\) then \(f_{x}(x,y)=\) \(f_{y}(x,y)\).

Question

For a function \(w=f(x,y,z)\) of three variables, to find the partial derivative \(f_{y}(x,y,z)\), treat the variables ____ and ____ as constants, and differentiate \(f\) with respect to ____.

Question

\(f(x,y)=x^{2}y+6y^{2}\)

Question

\(f(x,y)=3x^{2}+6xy^{3}\)

Question

\(f(x,y)=\dfrac{x-y}{x+y}\)

Question

\(f(x,y)=\dfrac{x+y}{y^{2}}\)

Question

\(f(x,y)=e^{y}\cos x+e^{x}\sin y\)

Question

\(f(x,y)=x^{2}\cos y+y^{2}\sin x\)

Question

\(f(x,y) =x^{2}e^{xy}\)

Question

\(f(x,y)=\cos (x^{2}y^{3})\)

Question

\(z= f(x,y)=\tan ^{-1}\dfrac{y}{x}\)

Question

\(z=f(x,y)=\sin ^{2}(2xy)\)

Question

\(z=f(x,y) =\sin ( e^{x^{2}y})\)

Question

\(z=f(x, y)=\sin [ \ln\;(x^{2}+y^{2})]\)

Question

\(z=f(x, y)=e^{( x^{2}+y^{2})^{1.2}}\)

Question

\(z=f(x,y)=\ln\;\sqrt{x^{2}+y^{2}}\)

Question

\(f(x,y)=6x^{2}-8xy+9y^{2}\)

Question

\(f(x,y)=(2x+3y) ( 3x-2y)\)

Question

\(f(x,y)=\ln\;(x^{3}+y^{2})\)

Question

\(f(x,y)=e^{2x+3y}\)

Question

\(f(x,y)=\cos (x^{2}y^{3})\)

Question

\(f(x,y)=\sin ^{2}(xy)\)

Question

\(f(x,y,z)=xy+yz+xz\)

Question

\(f(x,y,z)=xe^{y}+ye^{z}+ze^{x}\)

Question

\(f(x,y,z)=xy\;\sin\;z-yz\sin\;x\)

Question

\(f(x,y,z)=\dfrac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\)

Question

\(f(x,y,z)=z\;\tan ^{-1}\dfrac{y}{x}\)

Question

\(f(x,y,z)=\tan ^{-1}\dfrac{xy}{z}\)

Question

\(f(x,y,z)=\sin [\ln\;(x^{2}+y^{2}+z^{2})]\)

Question

\(f(x,y,z)=e^{x^{2}+y^{2}}\ln\;z\)

Question

\( f(x,y)=\left\{ \begin{array}{@{}c@{\quad}c@{\quad}c} \dfrac{x^{3}+y^{3}}{x^{2}+y^{2}} & \hbox{if} & (x,y)\neq (0,0)\\ 0 & \hbox{if} & (x,y)=(0,0) \end{array} \right.\)

Question

\(f(x,y)=\left\{ \begin{array}{@{}c@{\quad}c@{\quad}c} \dfrac{x^{2}y^{2}}{x^{2}+4y^{3}} & \hbox{if} & (x,y)\neq (0,0)\\ 0 & \hbox{if} & (x,y)=(0,0) \end{array} \right.\)

Question

\(z=x^{2}+y^{2}\) and \(y=2\) at \((1,2,5)\)

Question

\(z=x^{2}-y^{2}\) and \(x=3\) at \((3,1,8)\)

Question

\(z=\sqrt{1-x^{2}-y^{2}}\) and \(x=0\) at \(\left( 0,\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right)\)

Question

\(z=\sqrt{16-x^{2}-y^{2}}\) and \(y=2\) at \(( \sqrt{3},2,3)\)

Question

\(z=\sqrt{x^{2}+y^{2}}\) and \(x=4\) at \(( 4,2,2\sqrt{5})\)

Question

\(z=e^{x}\ln\;y\) and \(y=e\) at \((0,e,1)\)

Question

Find the rate of change of \(z=\ln\;\sqrt{x^{2}+y^{2}}\) at \((3,4,\ln\;5)\),

1. In the direction of the positive \(x\)-axis.
2. In the direction of the positive \(y\)-axis.

Question

Find the rate of change of \(z=e^{y}\sin x\) at \(\left( \dfrac{\pi }{3},0,\dfrac{\sqrt{3}}{2}\right)\! ,\)

1. In the direction of the positive \(x\)-axis.
2. In the direction of the positive \(y\)-axis.

Question

Temperature Distribution  The temperature distribution \(T\) (in degrees Celsius) of a heated plate at a point \((x,y)\) in the \(xy\)-plane is modeled by \[ T=T(x,y)=\left( \frac{100}{\ln\;2}\right)\;\ln\;(x^{2}+y^{2}) \qquad 1\leq x^{2}+y^{2}\leq 9 \]

1. Show that \(T=0\ ^{\circ}{\rm C}\) on the circle \(x^{2}+y^{2}=1\), and \(T=200\ ^{\circ}{\rm C}\) on the circle \(x^{2}+y^{2}=4\).
2. Find the rate of change of \(T\) in the direction of the positive \(x\)-axis at the point \((1,2)\) and at the point \((2,1)\). Describe the rate of change.
3. Find the rate of change of \(T\) in the direction of the positive \(y\)-axis at the point \((2,0)\) and at the point \((0,2)\). Describe the rate of change.

Question

Temperature Distribution  The temperature distribution (in degrees Celsius) of a heated plate at a point \((x,y)\) in the \(xy\)-plane is modeled by \( T=T(x,y)=\dfrac{100}{\sqrt{x^{2}+y^{2}}}\), \(1\leq x^2 + y^2\leq 9\).

1. Show that \(T=100{{}^{\circ}{\rm C}}\) on the circle \(x^{2}+y^{2}=1\), and \(T=50{ {}^{\circ}{\rm C}}\) on the circle \(x^{2}+y^{2}=4\).
2. Find the rate of change of \(T\) in the direction of the positive \(x\) -axis at the point \((1,0)\) and at the point \((0,1)\). Describe the rate of change.
3. Find the rate of change of \(T\) in the direction of the positive \(y\)-axis at the point \((2,0)\) and at the point \((0,2)\). Describe the rate of change.

Question

Thermodynamics  The Ideal Gas Law \(PV=nrT\) is used to describe the relationship between pressure \(P\), volume \(V\), and temperature \(T\) of a confined gas, where \(n\) is the number of moles of the gas and \(r\) is the universal gas constant. Show that \[ \dfrac{\partial V}{\partial T}\cdot \dfrac{\partial T}{\partial P}\cdot \dfrac{\partial P}{\partial V}=-1 \]

Question

Thermodynamics  The volume \(V\) of a fixed amount of gas varies directly with the temperature \(T\) and inversely with the pressure \(P\). That is, \(V=k\dfrac{T}{P},\) where \(k>0\) is a constant.

1. Find \(\dfrac{\partial V}{\partial T}\) and \(\dfrac{\partial V}{\partial P}\).
2. Show that \(T\,\dfrac{\partial V}{\partial T}+P\,\dfrac{\partial V}{\partial P}=0\).

Question

Economics  The data used to develop the Cobb–Douglas productivity model included capital input \(K\) and labor input \(L\) for each year during the period 1899–1922. Using the model \(P=aK^{b}L^{1-b}\) and multiple regression techniques, Cobb and Douglas determined that manufacturing productivity was represented by the function \[ P=1.014651K^{0.254124}L^{0.745876}\approx 1.01K^{0.25}L^{0.75} \]

1. Find the marginal productivity with respect to capital input and the marginal productivity with respect to labor input in 1900 when \(K=107\) and \(L=105.\)
2. Find the marginal productivity with respect to capital input and the marginal productivity with respect to labor input in 1920 when \(K=407\) and \(L=193.\)
3. Compare the answers. What do you conclude about the change in manufacturing productivity in the United States during the 20-year period?

Question

Economics  The function \[ z=f(x,y,r)=\frac{1+(1-x)y}{1+r}-1 \]

describes the net gain or loss of money invested, where \(x=\) annual marginal tax rate, \(y=\) annual effective yield on an investment, and \(r=\) annual inflation rate.

1. Find the annual net gain or loss if money is invested at an effective yield of \(4\%\) when the marginal tax rate is \(25\%\) and the inflation rate is \(5\%\); that is, find \(f(0.25,0.04,0.05)\).
2. Find the rate of change of gain (or loss) of money with respect to the marginal tax rate when the effective yield is \(4\%\) and the inflation rate is \(5\%\).
3. Find the rate of change of gain (or loss) of money with respect to the effective yield when the marginal tax rate is \(25\%\) and the inflation rate is \(5\%\).
4. Find the rate of change of gain (or loss) of money with respect to the inflation rate when the marginal tax rate is \(25\%\) and the effective yield is \(4\%\). Use \(r = 5\%\)

839

Question

Economics  Let \(w=2x^{1/2}y^{1/3}z^{1/6}\) be a production function that depends on three inputs: \(x,\) \(y,\) and \(z\). Find the marginal productivity with respect to \(x,\) the marginal productivity with respect to \(y,\) and the marginal productivity with respect to \(z.\)

Question

Speed of Sound  The speed \(v\) of sound in a gas depends on the pressure \(p\) and density \(d\) of the gas and is modeled by the formula \( v(p,d)=k\sqrt{\dfrac{p}{d}}\), where \(k\) is some constant. Find the rate of change of speed with respect to \(p\) and with respect to \(d\).

Question

Vibrating Strings  Suppose a vibrating string is governed by the equation \(f(x,t)=2\cos ( 5t) \sin x\), where \(x\) is the horizontal distance of a point on the string, \(t\) is time, and \(f(x,t)\) is the displacement. Show that \(\dfrac{\partial ^{2}f}{\partial t^{2}}=25\dfrac{ \partial ^{2}f}{\partial x^{2}}\) at all points \((x,t)\).

Question

Temperature Distribution  Suppose a thin metal rod extends along the \(x\)-axis from \(x=0\) to \(x=20\), and for each \(x\), where \(0\leq x\leq 20\), the temperature \(T\) of the rod at time \(t\geq 0\) and position \(x\) is \(T(t,x)=40e^{-\lambda t}\sin \dfrac{\pi x}{20}\), where \(\lambda >0\) is a constant.

1. Show that \(T_{t}=-\lambda T\), \(T_{xx}=-\dfrac{\pi ^{2}}{400}T\), and \(T_{t}=\dfrac{1}{k^{2}}T_{xx}\) for some \(k\).
2. Graph the initial temperature distribution, \(y=T(0,x),\) where \(0\leq x\leq 20\).

Question

Find \(\dfrac{\partial x}{\partial r}, \dfrac{\partial x}{\partial \theta }, \dfrac{\partial y}{\partial r}\), and \(\dfrac{\partial y}{\partial \theta }\) if \(x=r\cos \theta\) and \(y=r\;\sin \theta\).

Question

Find \(\dfrac{\partial r}{\partial x}, \dfrac{\partial \theta }{\partial x}, \dfrac{\partial r}{\partial y}\), and \(\dfrac{\partial \theta }{\partial y}\)

if \(r=\sqrt{x^{2}+y^{2}}\) and \(\theta =\tan^{-1}\dfrac{y}{x},\) \(x\neq 0.\)

Question

1. Graph \(f(x,y) =\dfrac{1}{2}x^{2}+\dfrac{1}{3}y^{2}\) and the plane \(y=1.\)
2. Find symmetric equations of the tangent line to the curve of intersection of the surface and the plane at the point \(\left( 2,1,\dfrac{7}{3}\right)\).

Question

1. Graph \(f(x,y) =\dfrac{5}{\sqrt{x^{2}+y^{2}+1}}\) and the plane \(x=1.\)
2. Find symmetric equations of the tangent line to the curve of intersection of the surface and the plane at the point \(\left( 1,-2,\dfrac{5\sqrt{6}}{6}\right)\).

Question

Show that \(\dfrac{\partial u}{\partial x}=\dfrac{\partial v}{\partial y}\) and \(\dfrac{\partial u}{\partial y}=-\dfrac{\partial v}{\partial x}\) for \(u=e^{x}\cos y\) and \(v=e^{x}\sin y\).

Question

Show that \(\dfrac{\partial u}{\partial x}=\dfrac{\partial v}{\partial y}\) and \(\dfrac{\partial u}{\partial y}=-\dfrac{\partial v}{\partial x}\) for \(u=\ln\;\sqrt{x^{2}+y^{2}}\) and \(v=\tan ^{-1}\dfrac{y}{x}\).

Question

If \(u=x^{2}+4y^{2}\), show that \(x\dfrac{\partial u}{\partial x}+y\dfrac{\partial u}{\partial y}=2u\).

Question

If \(u=xy^{2}\), show that \(x\dfrac{\partial u}{\partial x}+y \dfrac{\partial u}{\partial y}=3u\).

Question

If \(w=x^{2}+y^{2}-3yz\), show that \(x\dfrac{\partial w}{\partial x}+y\dfrac{\partial w}{\partial y}+z\dfrac{\partial w}{\partial z}=2w\).

Question

If \(w=\dfrac{xz+y^{2}}{yz}\), show that \(x\dfrac{\partial w}{\partial x}+y\dfrac{\partial w}{\partial y}+z\dfrac{\partial w}{\partial z}=0\).

Question

If \(z=\cos (x+y)+\cos (x-y)\), show that \(\dfrac{\partial ^{2}z}{\partial x^{2}}-\dfrac{\partial ^{2}z}{\partial y^{2}}=0\).

Question

If \(z=\sin (x-y)+\ln\;(x+y)\), show that \(\dfrac{\partial ^{2}z}{\partial x^{2}}=\dfrac{\partial ^{2}z}{\partial y^{2}}\).

Question

Show that \(u=e^{-\alpha ^{2}t}\sin \left( \alpha x\right)\) satisfies the equation \(\dfrac{\partial u}{\partial t}=\dfrac{\partial ^{2}u}{\partial x^{2}}\) for all values of the constant \(\alpha\).

Question

\(z=\ln\;\sqrt{x^{2}+y^{2}}\)

Question

\(z=e^{ax}\sin ( ay)\)

Question

\(z=\tan ^{-1}\dfrac{y}{x}\)

Question

\(z=e^{ax}\cos ( ay)\)

Question

Harmonic Functions  Suppose \(u(x,y)\) and \(v(x,y)\) have continuous second-order partial derivatives, \(u_{x}=v_{y}\) and \(u_{y}=-v_{x}\). Show that \(u\) and \(v\) are harmonic functions.

Question

Harmonic Functions  If \(u=z\tan ^{-1}\dfrac{x}{y}\), show that \[ \dfrac{\partial ^{2}u}{\partial x^{2}}+\dfrac{\partial ^{2}u}{\partial y^{2}} +\dfrac{\partial ^{2}u}{\partial z^{2}}=0. \]

Question

Harmonic Functions  Show that \(f(x,y,z)=(x^{2}+y^{2}+z^{2})^{-1/2}\) satisfies the three-dimensional Laplace equation \[ f_{xx}+f_{yy}+f_{zz}=0 \]

Question

Let \(f(x,y)=\left\{ \begin{array}{@{}c@{\quad}c@{\quad}c} \dfrac{xy^{3}}{x^{2}+y^{2}} & \hbox{if} & (x,y)\neq (0,0) \\ 0 & \hbox{if} & (x,y)=(0,0) \end{array} \right.\)

1. Find \(f_{x}\) and \(f_{y}\). [Hint: \(f_{x}\) and \(f_{y}\), where \((x,y)\neq (0,0)\), can be found using derivative formulas. To find \(f_{x}(0,0)\) and \(f_{y}(0,0)\), use the definition of a partial derivative.]
2. Show that \(f_{xy}(0,0)\neq f_{yx}(0,0)\).

Question

Let \(f(x,y)=\left\{ \begin{array}{@{}c@{\quad}c@{\quad}c} \dfrac{xy(x^{2}-y^{2})}{x^{2}+y^{2}} & \hbox{if} & (x,y)\neq (0,0) \\ 0 & \hbox{if} & (x,y)=(0,0) \end{array} \right.\)

Show that:

1. \(f_{x}(0,y)=-y\)
2. \(f_{y}(x,0)=x\)
3. \(f_{xy}(0,0)=-1\)
4. \(f_{yx}(0,0)=1\)

Question

If you are told that \(f\) is a function of two variables whose partial derivatives are \(f_{x}(x,y)=3x-y\) and \(f_{y}(x,y)=x-3y\), should you believe it? Explain.

*Laplace’s equation is important in many applications including fluid dynamics, heat, elasticity, and electricity.

840

Question

Show that there is no function \(z=f(x,y)\) for which \(f_{x}(x,y)=2x-y\) and \(f_{y}(x, y)=x-2y\).

Question

Use the definition of a partial derivative to show that the function \(z=\sqrt{x^{2}+y^{2}}\) does not have partial derivatives at \((0,0)\). By discussing the graph of the function, give a geometric reason why this should be so.

Question

If \(z=f(x,y)=4x^{2}+9y^{2}-12\), interpret \(f_{x}\left( 1,-\dfrac{1}{3}\right)\) and \(f_{y}\left( 1,-\dfrac{1}{3}\right)\) geometrically.

Question

Show that \(xf_{x}+yf_{y}+zf_{z}=0\) for \(f(x,y,z)= e^{x/y}+e^{y/z}+e^{z/x}\).

Question

Find \(a\) in terms of \(b\) and \(c\) so that \(f(t,x,y)= e^{at}\sin\;(bx)\;\cos\;(cy)\) satisfies \(f_{t}=f_{xx}+f_{yy}\).

Question

Wave Equation  Show that \(f(x,t)=\cos (x+ct)\) satisfies the one-dimensional wave equation \(f_{tt}=c^{2}f_{xx}\), where \(c\) is a constant.

Question

Find \(f_{x}\) and \(f_{y}\) if \(f(x, y)=\int_{x}^{y}\ln\;(\cos\;\sqrt{t})\ dt\).

Question

Find \(\dfrac{\partial a}{\partial b}\), \(\dfrac{\partial a}{\partial c}\), and \(\dfrac{\partial a}{\partial A}\) for the Law of Cosines: \(a^{2}=b^{2}+c^{2}-2bc\;\cos\;A\).

Question

If \(x=r\cos\;\theta\) and \(y=r\sin\;\theta\), show that \[ \begin{equation*} \left\vert \begin{array}{c@{\quad}c} \dfrac{\partial x}{\partial r} & \dfrac{\partial x}{\partial \theta } \\ \dfrac{\partial y}{\partial r} & \dfrac{\partial y}{\partial \theta } \end{array} \right\vert =r \qquad\hbox{and}\qquad \left\vert \begin{array}{c@{\quad}c} \dfrac{\partial r}{\partial x} & \dfrac{\partial r}{\partial y} \\ \dfrac{\partial \theta }{\partial x} & \dfrac{\partial \theta }{\partial y} \end{array} \right\vert =\frac{1}{r} \end{equation*} \]

Question

\(f(x,y) =x^{y}\)

Question

\(f(x,y)=x^{2x+3y}\)

Question

\(f(x,y,z)=x^{y+z}\)

Question

\(f(x,y,z)=x^{yz}\)

Question

\(f(x,y,z)=(x+y)^{z}\)

Question

\(f(x,y,z)=(xy) ^{z}\)

Question

Find \(f_{x}\) and \(f_{y}\) at \((0,0)\) if \[ f(x, y)=\left\{ \begin{array}{@{}c@{\quad}c@{\quad}c} e^{-1/(x^{2}+y^{2})} & \hbox{if} & (x,y)\neq (0,0)\\ 0 & \hbox{if} & (x,y)=(0,0) \end{array} \right. \]

Question

Find \(f_{x},\) \(f_{y},\) \(f_{xx},\) \(f_{yy}\), and \(f_{xy}\) for \(f(x,y)=(xy)^{xy}\). What is the domain of \(f\)?

Question

Show that the following function has first partial derivatives at all points in the plane: \[ f(x,y)=\left\{ \begin{array}{@{}c@{\quad}c@{\quad}c} \dfrac{x^{3}-y^{3}}{x^{2}+y^{2}} & \hbox{if} & (x,y)\neq (0,0)\\ 0 & \hbox{if} & (x,y)=(0,0) \end{array} \right. \]

Question

Laplace’s Equation in Polar Coordinates  Show that the function \(f(r,\theta )=r^{n}\sin ( n\theta )\) satisfies the Laplace equation \[ f_{r\,r}+\dfrac{1}{r}\,f_{r}+\dfrac{1}{r^{2}}\,f_{\theta \,\theta }=0 \]

Question

Let \(u=r^{m}\cos ( m\theta )\). Show that \[ \dfrac{\partial ^{2}u}{\partial r^{2}}+\dfrac{1}{r^{2}}\left( \dfrac{ \partial ^{2}u}{\partial \theta ^{2}}\right) +\dfrac{1}{r}\left(\dfrac{ \partial u}{\partial r}\right) = 0\;{\rm for\;all}\;m. \]

Question

1. Find symmetric equations of the tangent lines at \(( x_{0},y_{0}, f(x_{0},y_{0}))\) to the curve of intersection of \(z=f(x,y)\) and \(y=y_{0}\), and the curve of intersection of \(z=f(x, y)\) and \(x=x_{0}\).
2. Write an equation of the plane determined by these two lines.
3. What is the geometric relationship of this plane to the surface \(z=f(x, y)\)?

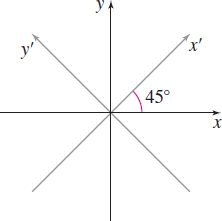
Question

Consider two coordinate systems as given in the figure.

1. Let \(f(x,y)=3x^{2}+4y^{3}\). Find \(f_{x}(1,6)\) and \(f_{y}(1,6)\).
2. Let \((a,b)\) be the \(x^{\prime }y^{\prime }\)-coordinates of \((1,6)\). Let \(\bar{f}(x^{\prime },y^{\prime })=f(x,y)\). Find \(\bar{f}_{x^{\prime }}(a,b)\) and \(\bar{f}_{y^{\prime }}(a,b)\).