12.4 Differentiability and the Differential
OBJECTIVES
When you finish this section, you should be able to:
- Find the change in \(z \,=\, f( x, y)\) (p. 841)
- Show that a function of two variables is differentiable (p. 841)
- Use the differential \(dz\) to approximate a change in \(z\) (p. 844)
- Find the differential of a function of three or more variables (p. 846)
For a function \(y=f(x)\) of a single variable, we said that when \(f\) has a derivative, then \(f\) is differentiable. We also defined the differential of \(y\) in terms of its derivative as \(dy=f' (x)\ dx,\) where \(dx=\Delta x.\) For functions of more than one variable, the situation is a little more involved. We begin by defining what it means for a function \(z=f(x,y)\) to be differentiable, which involves the change \(\Delta z\) in \(z.\) Then under suitable conditions on \(z\) , we will define \(dz,\) the differential of \(z.\)
1 Find the Change in \(z=f(x,y)\)
841
If \(y=f(x)\) is a function of one variable, then the change \(\Delta y\) in \(y\) from \(x_{0}\) to \(x_{0}+\Delta x\) is \[ \Delta y=f( x_{0}+\Delta x) -f( x_{0}) \]
There is a similar definition for a function \(z=f(x,y)\) of two variables.
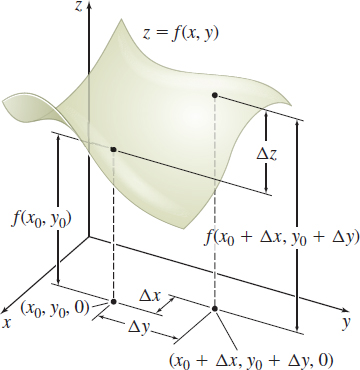
spanDEFINITIONspan Change in \(z=f(x,y)\)
Let \(z=f(x,y)\) be a function of two variables with domain \(D\). Let \((x_{0},y_{0})\) be an interior point of \(D\), and let \(\Delta x\) and \(\Delta y\) represent changes in \(x\) and in \(y\), respectively. If \(\Delta x\) and \(\Delta y\) are chosen so that the point \((x_{0}+\Delta x, y_{0}+\Delta y)\) is also in \(D\), then the change in \(z\), denoted by \(\Delta z\), is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \Delta z=f(x_{0}+\Delta x, y_{0}+\Delta y)-f(x_{0}, y_{0})}} \]
See Figure 36.
Finding the Change in \(z\)
- Find the change \(\Delta z\) in \(z=f(x,y)=x^{2}y-1\) from \((x_{0},y_{0})\) to \((x_{0}+\Delta x, y_{0}+\Delta y)\).
- Use the answer to calculate the change in \(z\) from \((1,2)\) to \((1.1,1.9)\).
Solution (a) \[ \begin{eqnarray*} \Delta z&=&f(x_{0}+\Delta x, y_{0}+\Delta\;y)-f(x_{0},y_{0})\nonumber\\ &=& [ (x_{0}+\Delta x)^{2}(y_{0}+\Delta y)-1]-[ x_{0}^{2}\,y_{0}-1] \end{eqnarray*} \]
(b) Let \((x_{0},y_{0}) =(1,2)\) and \((x_{0}+\Delta x,y_{0}+\Delta y) =( 1.1,1.9)\). Then \[ \Delta z=[ ( 1.1) ^{2}( 1.9) -1] -[(1) ^{2}( 2) -1] =0.299 \]
NOW WORK
Problem 7.
2 Show That a Function of Two Variables Is Differentiable
NEED TO REVIEW?
The differentials \(dx\) and \(dy\) of a function \(y=f (x)\) of one variable are discussed in Section 3.4, pp. 230-232.
Before defining the differentiability of a function of two variables, let’s reexamine the differential \(dy\) of a function \(y=f(x)\) of a single variable. For a differentiable function \(y=f(x)\) of one variable, the differentials \(dx=\Delta x\) and \(dy=f' (x)\ dx=f' (x) \Delta x\) can be used to approximate \(\Delta y=f(x_{0}+\Delta x)-f(x_{0}).\) That is, \[ dy\approx \Delta y=f(x_{0}+\Delta x)-f(x_{0}) \]
provided \(\Delta x\) is close to \(0.\)
NOTE
\(\eta\) is the Greek letter eta.
If the error in using \(dy\) to approximate \(\Delta y\) is \(\eta \Delta x\), then \[ \begin{eqnarray*} \Delta y-dy &=&\eta \Delta x \nonumber \\[4pt] \Delta y &=&f' (x_{0})\Delta x+\eta \Delta x \qquad\quad {\color{#0066A7}{\hbox{\(dy=f' (x_{0}) \Delta x\)}}} \tag{1} \end{eqnarray*} \]
where \(\eta\) is a function of \(\Delta x\) for which \(\lim\limits_{\Delta x\rightarrow 0}\eta =0\).
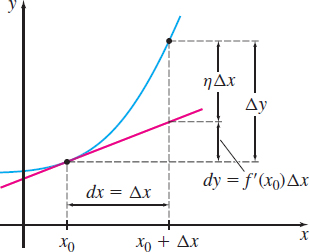
Figure 37 gives a geometric interpretation of equation (1). From Figure 37, we can see that \(\eta \Delta x\rightarrow 0\) as \(\Delta x\rightarrow 0\). But Figure 37 does not show something else suggested by equation (1), namely that \(\eta \rightarrow 0\) as \(\Delta x\rightarrow 0\). Do you see why? From (1), \(\dfrac{\Delta y}{\Delta x}=f' \left( x_{0}\right) +\eta .\) Since \(f\) is differentiable, \(\lim\limits_{\Delta x\rightarrow 0}\dfrac{\Delta y}{\Delta x}=f' (x_{0}).\) This means \(\lim\limits_{\Delta x\rightarrow 0}\eta\) must be \(0.\)
The discussion above provides background for the definition of differentiability of a function of two variables.
842
spanDEFINITIONspan Differentiability of \(z=f(x,y)\) at \((x_{0},y_{0})\)
Let \(z=f(x,y)\) be a function of two variables whose domain is \(D\). Let \((x_{0},y_{0})\) be an interior point of \(D\) and let \(\Delta x\) and \(\Delta y\) be chosen so that the point \((x_{0}+\Delta x, y_{0}+\Delta y)\) is also in \(D\). If the change \(\Delta z\) from \((x_{0},y_{0})\) to \((x_{0}+\Delta x,y_{0}+\Delta y)\) can be expressed in the form \[ \begin{equation*}{\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \Delta z=f_{x}(x_{0},y_{0})\Delta x+f_{y}(x_{0},y_{0})\Delta y+\eta _{1}\Delta x+\eta _{2}\Delta y }}} \tag{2} \end{equation*} \]
where both \(\eta _{1}\) and \(\eta _{2}\) are functions of \(\Delta x\) and \(\Delta y\) for which \[ \begin{equation*} \lim\limits_{(\Delta x, \Delta y)\rightarrow (0,\, 0)}\eta _{1}=0\qquad \hbox{and}\qquad \lim\limits_{(\Delta x, \Delta y)\rightarrow (0,\, 0)}\eta _{2}=0 \tag{3} \end{equation*} \]
then \(z=f(x,y)\) is said to be differentiable at the point \((x_{0},y_{0})\).
If the domain \(D\) of a function \(z=f(x,y)\) is an open set and if \(z=f(x,y)\) is differentiable at every point of \(D\), then we say \(f\) is differentiable on \(D\).
Showing That a Function of Two Variables Is Differentiable
Show that \(z=f(x, y)=x^{2}y-1\) is differentiable.
Solution The domain of \(f\) is the \(xy\)-plane and the partial derivatives of \(f\) are \[ f_{x}(x,y) =2xy\qquad \hbox{and}\qquad f_{y}(x,y) =x^{2} \]
We find the change \(\Delta z\) in \(z\) and express it in the form of (2). \[ \begin{eqnarray*} \Delta z &=& [ (x+\Delta x)^{2}(y+\Delta y)-1 ] - [ x^{2}y-1 ]\\ &=& [ x^{2}+2x\Delta x+ ( \Delta x ) ^{2} ] ( y+\Delta y ) - x^{2}y \\ &=&x^{2}\Delta y+2xy\Delta x+2x\Delta x\Delta y+y(\Delta x)^{2}+(\Delta x)^{2}\Delta y \\ &=&\underset{\color{#0066A7}{\hbox{\(f_{x}(x,y)\)}}}{\underbrace{ ( 2xy ) }}\Delta x+\! \underset{\color{#0066A7}{\hbox{\(f_{y}(x,y)\)}}}{\underbrace{ ( x^{2} ) }} \Delta y+\,\underset{\color{#0066A7}{\hbox{\(\eta _{1}\)}}}{\underbrace{ [ y\Delta x ] }}\Delta x+\,\underset{\color{#0066A7}{\hbox{\(\eta _{2}\)}}}{\underbrace{ [ 2x\Delta x+(\Delta x)^{2} ] }}\Delta y\\ &=&f_{x}(x,y) \Delta x+f_{y}(x,y) \Delta y+\eta _{1}\Delta x+\eta _{2}\Delta y \end{eqnarray*} \]
Equation (2) is satisfied. It remains to show that equation (3) is satisfied. \[ \lim_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{1}=\lim_{\Delta x\rightarrow 0}( y\Delta x) =0\quad\!\! \hbox{and}\!\!\quad \lim_{( \Delta x,\Delta y) \rightarrow (0,0) }\eta _{2}=\lim_{\Delta x\rightarrow 0}[ 2x\Delta x+(\Delta x)^{2}] =0 \]
So, \(z=f(x,y)\) is differentiable on its domain.
NOTE
There are other ways to choose \(\eta _{1}\) and \(\eta _{2}\) so that equations (2) and (3) are satisfied.
NOW WORK
Problem 29.
Although not every function \(z=f(x,y)\) is differentiable, there are conditions on a function \(z=f(x,y)\) that will guarantee it is differentiable.
THEOREM Continuous Partial Derivatives Are Sufficient for Differentiability
Let \(z=f(x,y)\) be a function of two variables whose domain is \(D\). Let \((x_{0},y_{0})\) be an interior point of \(D\). If the partial derivatives \(f_{x}\) and \(f_{y}\) exist at each point of some disk centered at \((x_{0},y_{0})\), and if \(f_{x}\) and \(f_{y}\) are each continuous at \((x_{0},y_{0})\), then \(f\) is differentiable at \((x_{0},y_{0})\).
The proof of this result is given in Appendix B.
Now we are ready to define the differential \(dz\) of a function \(z=f(x,y)\).
843
spanDEFINITIONspan Differential \(dz\) of \(z=f(x,y)\)
Let \(z=f(x,y)\) be a function of two variables whose domain is \(D\). Let \((x_{0},y_{0})\) be an interior point of \(D\) and let \(\Delta x\) and \(\Delta y\) be chosen so that the point \((x_{0}+\Delta x,y_{0}+\Delta y)\) is also in \(D\). If \(f\) is differentiable at the point \((x_{0},y_{0})\), then the differentials \(dx\) and \(dy\) are defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ dx=\Delta x\qquad \hbox{and}\qquad dy=\Delta y }} \]
The differential \(dz\), also called the total differential of \(z=f(x,y)\) at \((x_{0},y_{0})\), is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ dz=f_{x}(x_{0},y_{0})\,dx+f_{y}(x_{0},y_{0})\,dy }} \]
Finding the Differential \(dz\) of \(z=f(x,y)\)
Find the differential \(dz\) of each function:
- \(f(x,y) =e^{x}\cos\;y\)
- \(f(x,y) =\dfrac{\ln\;x}{y}\)
Solution (a) \(f\) is defined everywhere in the \(xy\)-plane. The partial derivatives of \(f\) are \[ \begin{equation*} f_{x}(x,y) =e^{x}\cos\;y\qquad f_{y}(x,y) =-e^{x}\;\sin\;y \end{equation*} \]
Since \(f_{x}\) and \(f_{y}\) are continuous everywhere in the \(xy\)-plane, the function \(z=f(x,y)\) is differentiable. The differential \(dz\) is \[ dz=e^{x}\cos\;y\,dx-e^{x}\sin\;y\,dy \]
(b) The domain of \(f\) is \(\left\{(x,y) \,|\,x>0,\,y\neq 0\right\} .\) The partial derivatives of \(f\) are \[ f_{x}(x,y) =\dfrac{1}{xy}\qquad f_{y}(x,y) =-\dfrac{\ln\;x}{y^{2}} \]
Since both partial derivatives exist and are continuous at every point \((x_{0},y_{0})\) in the domain of \(f\), the function \(z=f(x,y)\) is differentiable at every point \((x_{0},y_{0})\) in its domain. The differential \(dz\) is \[ dz=\dfrac{1}{xy}\, dx-\dfrac{\ln\;x}{y^{2}}\,dy \]
NOW WORK
Problem 11.
If \(z=f(x,y)\) is a differentiable function, then \(\Delta z\) can be expressed in terms of the differential \(dz.\) 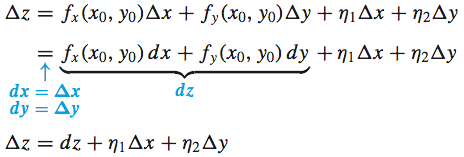
where \(\lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{1}=0\) and \(\lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{2}=0\).
When the differentials \(dx=\Delta x\) and \(dy=\Delta y\) are close to \(0,\) then \(\eta _{1}\) and \(\eta _{2}\) are also close to \(0,\) and the differential \(dz\) is approximately equal to \(\Delta z\). That is, \[ \begin{equation*}{ \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \Delta z\approx dz=f_{x}(x_{0},y_{0})\,dx+f_{y}(x_{0},y_{0})\,dy }}} \tag{4} \end{equation*} \]
The differential \(dz\) is usually easier to calculate than \(\Delta z\), making \(dz\) a useful approximation to \(\Delta z\). The error introduced in using \(dz\) to approximate \(\Delta z\) equals the expression \(\eta _{1}\Delta x+\eta _{2}\Delta y\).
3 Use the Differential \(dz\) to Approximate a Change in \(z\)
844
Using the Differential \(dz\) to Approximate the Change in \(z\)
For the function \(z=f(x, y)=x^{2}y-1,\) use the differential \(dz\) to approximate the change in \(z\) from \((1,2)\) to \((1.1,1.9)\).
Solution Example 2 shows \(f\) is differentiable and \(f_{x}(x,y) =2xy\) and \(f_{y}(x,y) =x^{2}.\)
Let \(( x_{0},y_{0}) =( 1,2)\) and \(( x_{0}+\Delta x,y_{0}+\Delta y) =( 1.1,1.9) .\) Then \[ dx=\Delta x=1.1-1=0.1, \hbox{ and } dy=\Delta y=1.9-2= -0.1. \]
Using (4), an approximation to the change in \(z\) is \[ \Delta z\approx dz=f_{x}(1,2)\,dx+f_{y}(1,2)\,dy=2(1) (2) ( 0.1) +(1) ( -0.1) =0.4-0.1=0.3 \]
The actual change in \(z\) was computed in Example 1 to be \(0.299\), so using the differential \(dz\) to approximate \(\Delta z\) results in an error of 0.001.
NOW WORK
Problem 33.
Using the Differential in Astronomy
The luminosity \(L\) (total power output in watts, W) of a star is given by the formula \[ L=L( R,T) =4\pi R^{2}\sigma T^{4} \]
where \(R\) is the radius of the star (in meters), \(T\) is its effective surface temperature (in kelvin, K), and \(\sigma\) is the Stefan–Boltzmann constant. For the sun, \(L_{s}=(3.90\times\;10^{26})\) \(\rm{W}\), \(R_{s}=(6.94\times\;10^{8})\;\rm{m}\) , and \(T_{s}=4800\;\rm{K}\). Suppose in a billion years, the changes in the Sun will be \(\Delta R_{s}=(0.08\;\times\;10^{8})\;\rm{m}\) and \(\Delta T_{s}=100\;\rm{K}\). What will be the resulting percent increase in luminosity?
Solution We begin with \(L=4\pi\;R^{2}\sigma\;T^{4}.\) Then \[ dL=4\pi \sigma (2R) T^{4}dR+4\pi \sigma R^{2}( 4T^{3}) dT=8\pi \sigma RT^{3}( T dR+2R\ dT) \]
The relative error in luminosity is \[ \begin{eqnarray*} \frac{\Delta L}{L}&\approx& \frac{dL}{L}=\dfrac{8\pi \sigma RT^{3}}{4\pi R^{2}\sigma T^{4}}\left( TdR+2RdT\right) =2\left( \frac{dR}{R}+2\frac{dT}{T} \right) =2\frac{\Delta R}{R}+4\frac{\Delta T}{T}\\[4pt] &=&\frac{2(0.08\times 10^{8})}{6.94\times 10^{8}}+\frac{4(100)}{4800}\approx 0.106 \end{eqnarray*} \]
The percent increase in luminosity will be approximately \(10.6\%\).
Incidentally, a reasonable, although rough, estimate of how this change would affect Earth’s temperature is \[ \Delta T_{e}\approx \left( \frac{1}{4}\right) (0.106)T_{e}=(0.0265)(290\rm{K})\approx 7.69\rm{K} \]
That is, the average temperature of Earth’s surface will change from 16.9 \(^{\circ}{\rm C}\) (62.4\(^{\circ}{\rm F}\)) to 24.6\(^{\circ}{\rm C}\) (76.3\(^{\circ}{\rm F}\)). Such a change in temperature would be enough to modify Earth’s climate.

Using the Differential in Error Analysis
A cola company requires a can in the shape of a right circular cylinder of height \(10~\rm{cm}\) and radius \(3~\rm{cm}\). If the manufacturer of the cans claims a percentage error of no more than \(0.2\%\) in the height and no more than \(0.1\%\) in the radius, what is the approximate maximum variation in the volume of the can?
845
Solution The volume \(V\) of a right circular cylinder of height \(h~\rm{cm}\) and radius \(R\;\rm{cm}\) is \(V=\pi\;R^{2}h\;\rm{cm}^{3}\). We find the differential \(dV.\) \[ dV=\frac{\partial V}{\partial R}dR+\frac{\partial V}{\partial h}dh=2\pi\;Rh\,dR+\pi\;R^{2}dh \]
The relative error in the radius \(R\) is \(\dfrac{|\Delta R|}{R}=\dfrac{|dR|}{R}=0.001\), and the relative error in the height \(h\) is \(\dfrac{\left\vert \Delta h\right\vert }{h}=\dfrac{|dh|}{h}=0.002\). The relative error in the volume \(V\) is \[ \begin{eqnarray*} \frac{|\Delta V|}{V} &\approx &\frac{|dV|}{V}=\frac{\left\vert 2\pi Rh\, dR+\pi R^{2} dh\right\vert }{\pi R^{2}h}=\left\vert 2\dfrac{dR}{R}+\dfrac{dh}{h}\right\vert\\[4pt] &=&\left\vert 2\dfrac{\Delta R}{R}+\dfrac{\Delta h}{h} \right\vert \leq 2\frac{\left\vert \Delta R\right\vert }{R}+\frac{\left\vert \Delta h\right\vert }{h} \\ &=&2(0.001)+0.002=0.004 \end{eqnarray*} \]
The maximum variation in the volume is approximately \(0.4\%\), so the actual volume of the container varies as follows: \[ \begin{equation*} V=\pi R^{2}h\pm 0.004( \pi R^{2}h) =\pi R^2 h ( 1\pm 0.004) =90\pi ( 1\pm 0.004) \rm{cm}^{3} \end{equation*} \]
The volume \(V\) is between \(89.64\pi \approx 281.612\;\rm{cm}^{3}\) and \(90.36\pi \approx 283.874\rm{cm}^{3}\).
NOW WORK
Problem 39.
Continuity and Differentiability for Functions of Two Variables
Differentiable functions of a single variable are necessarily continuous. This result is also true for functions of two variables.
THEOREM Differentiability Is Sufficient for Continuity
Let \(z=f(x,y)\) be a function of two variables whose domain is \(D\). Let \((x_{0},y_{0})\) be an interior point of \(D\). If \(f\) is differentiable at \((x_{0},y_{0})\), then \(f\) is continuous at \((x_{0},y_{0})\).
Proof
The function \(z=f(x,y)\) is continuous at \((x_{0},y_{0})\) if \(\lim\limits_{(x,y) \rightarrow (x_{0},y_{0}) }f(x,y) =f(x_{0},y_{0}) .\) This is equivalent to the statement \(\lim\limits_{(x,y) \rightarrow (x_{0},y_{0}) }\Delta z=0.\) Since \(z=f(x,y)\) is differentiable at \((x_{0},y_{0})\), then \(\Delta z\) can be expressed as \[ \begin{equation*} \Delta z=f_{x}(x_{0},y_{0})\Delta x+f_{y}(x_{0},y_{0})\Delta y+\eta _{1}\Delta x+\eta _{2}\Delta y \end{equation*} \]
where \(\lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{1}=0\) and \(\lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{2}=0\). Then \[ \begin{equation*} \Delta z=\left[ f_{x}(x_{0}, y_{0})+\eta _{1}\right] \,\Delta x+\left[ f_{y}(x_{0}, y_{0})+\eta _{2}\right] \,\Delta y \end{equation*} \]
Now let \(\Delta x=x-x_{0}\) and \(\Delta y=y-y_{0}\). Then \((\Delta x,\Delta y)\rightarrow (0, 0)\) is equivalent to \((x,y)\rightarrow (x_{0}, y_{0})\) and \[ \begin{eqnarray*} \lim_{(x, y)\rightarrow (x_{0}, y_{0})}\Delta z&=&\lim_{(x, y)\rightarrow (x_{0}, y_{0})}\{ [ f_{x}(x_{0}, y_{0})+\eta _{1} ] (x-x_{0} )\\[4pt] &&+\, [ f_{y}(x_{0}, y_{0})+\eta _{2} ](y-y_{0})\} =0 \end{eqnarray*} \]
That is, \(f\) is continuous at \((x_{0},y_{0})\).
For functions of two variables, differentiability implies continuity. However, the existence of partial derivatives at a point does not necessarily result in continuity at that point because \(f_{x}\) and/or \(f_{y}\) might not be continuous at the point. For example, the function \[ \begin{equation*} f(x,y)=\left\{ \begin{array}{@{}c@{\quad}c@{\quad}c} \dfrac{xy}{x^{2}+y^{2}} & \hbox{if} & (x,y)\neq (0,0) \\ {\small 0} & \hbox{if} & (x,y)=(0,0) \end{array} \right. \end{equation*} \]
846
has partial derivatives at \((0,0) ,\) but as shown in Example 8 on page 835, \(f\) is not continuous at \((0,0)\).
A function that is differentiable at \((x_{0},y_{0})\) is continuous at \((x_{0},y_{0}) .\) So, a function that is not continuous at \((x_{0},y_{0})\) is not differentiable at \((x_{0},y_{0})\).
The following corollary provides a condition for \(z=f(x,y)\) to be continuous.
COROLLARY Continuity of a Function of Two Variables
Let \(z=f(x,y)\) be a function of two variables whose domain is \(D\). Let \((x_{0},y_{0})\) be an interior point of \(D\). If the partial derivatives \(f_{x}\) and \(f_{y}\) exist at each point of some disk centered at \((x_{0},y_{0})\), and if \(f_{x}\) and \(f_{y}\) are each continuous at \((x_{0},y_{0})\), then \(f\) is continuous at \((x_{0},y_{0})\).
Although the precise formulations are given as theorems, the following summary might be helpful:
If \(z=f(x,y)\),
- The continuity of the partial derivatives \(f_{x}\) and \(f_{y}\) implies the differentiability of \(f\).
- The differentiability of \(f\) implies the continuity of \(f\).
- The continuity of the partial derivatives \(f_{x}\) and \(f_{y}\) implies the continuity of \(f\).
- The existence of the partial derivatives \(f_{x}\) and \(f_{y}\) does not necessarily mean \(f\) is differentiable.
- The existence of the partial derivatives \(f_{x}\) and \(f_{y}\) does not necessarily mean \(f\) is continuous.
4 Find the Differential of a Function of Three or More Variables
Under suitable conditions, the definitions and theorems involving the differentiability of a function of two variables extend to functions of three or more variables. If \(w=f(x,y,z)\) is a function of three variables, the function \(f\) is differentiable at a point \((x_{0},y_{0},z_{0})\) if the change \(\Delta w\) in \(w\) can be expressed in the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \Delta w=f_{x}(x, y, z)\Delta x+f_{y}(x, y, z)\Delta y+f_{z}(x, y, z)\Delta z+\eta _{1}\Delta x+\eta _{2}\Delta y+\eta _{3}\Delta z }} \]
where \(\eta _{1}, \eta _{2}\), and \(\eta _{3}\) are each functions of \(\Delta x, \Delta y\), and \(\Delta z\) for which \[ \lim_{(\Delta x, \Delta y, \Delta z)\rightarrow (0, 0, 0)}\eta _{1}=0\quad\hbox{and}\!\!\quad \lim_{(\Delta x, \Delta y, \Delta z)\rightarrow (0, 0, 0)}\eta _{2}=0\quad\hbox{and}\!\!\quad \lim_{(\Delta x, \Delta y, \Delta z)\rightarrow (0, 0, 0)}\eta _{3}=0 \]
If \(w=f(x,y,z)\) is differentiable at a point \((x_{0},y_{0},z_{0})\), the differentials \(dx,\) \(dy,\) and \(dz\) are defined as \[ dx=\Delta x\qquad dy=\Delta y \qquad dz=\Delta z \]
The differential \(dw\) is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ dw=f_{x}(x_{0},y_{0},z_{0})\ dx+f_{y}(x_{0},y_{0},z_{0})\ dy+f_{z}(x_{0},y_{0},z_{0})\ dz }} \]
It can be shown that if \(w=f(x,y,z)\) is defined within a ball centered at \((x_{0},y_{0},z_{0})\), and if the partial derivatives \(f_{x}\), \(f_{y}\), and \(f_{z}\) exist in this ball and are continuous at \((x_{0},y_{0},z_{0})\), then \(f\) is differentiable at \((x_{0},y_{0},z_{0})\).
Finding the Differential of a Function of Three Variables
Find the differential \(dw\) of the function \(w=f(x,y,z)=3x^{2}\sin ^{2}y\cos z\).
Solution The function \(f\) is defined everywhere in space. We begin by finding the partial derivatives of \(f.\) \[ \begin{eqnarray*} f_{x}(x,y,z) &=&6x\;\sin^{2}\;\!y\;\cos\;z\qquad f_{y}(x,y,z) =6x^{2}\;\sin\;y\;\cos\;y\cos\;z\\ f_{z}(x,y,z) &=&-3x^{2}\sin^{2}\;\!y\;\sin\;z \end{eqnarray*} \]
847
Since the partial derivatives are continuous everywhere, we have \[ \begin{eqnarray*} dw&=&f_{x}(x,y,z)\ dx+f_{y}(x,y,z)\ dy+f_{z}(x,y,z)\ dz\\ &=&6x\;\sin^{2}\;\!y\;\cos\;z\,dx+6x^{2}\;\sin\;y\;\cos\;y\;\cos\;z\,dy-3x^{2}\;\sin^{2}\;\!y\;\sin\;z\,dz \end{eqnarray*} \]
NOW WORK
Problem 23.
The discussion above extends to functions of more than three variables in an analogous way.