Question

True or False Suppose \(R\) is a closed, rectangular region in the \(xy\)-plane with sides of length \(\Delta x\) and \( \Delta y\). If the perimeter of \(R\) is projected upward parallel to the \(z\) -axis, the result is a cylinder. If \(S_{p}\) is the area cut from the plane \( z=ax+by+c\) by this cylinder, then \(S_{p}=\sqrt{a^{2}+b^{2}+1}\,\Delta x\Delta y\).

Question

True or False Suppose \(z=f(x,y)\) is a function of two variables defined on a closed, bounded region \(R\). If \(f_{x}\) and \(f_{y}\) are continuous on \(R\), then the area \(S\) of the part of the surface that lies over \(R\) is given by \(S=\displaystyle\iint\limits_{\kern-3ptR}\sqrt{f_{x}(x,y)+f_{y}(x,y)+1 }d\!A\).

Question

Find the surface area of the part of the plane \(2x+2y+z=6\) that lies above the region in the \(xy\)-plane bounded by \(x^{2}+y^{2}=4,\) the \(x\)-axis, and the \(y\)-axis, as shown in the figure.

Question

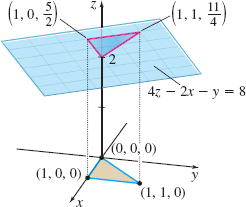
Find the surface area of the part of the plane \(4z-2x-y=8\) that lies over the region enclosed by the triangle with vertices \((0,0,0)\), \((1,0,0)\), and \(( 1,1,0)\), as shown in the figure.

Question

The part of the surface \(z=f(x,y) =\sqrt{ 9-x^{2}}\) that lies above the rectangle enclosed by the lines \(x=0,\) \(x=2,\) \( y=-1,\) \(y=4\)

Question

The part of the surface \(z=f(x,y) =\sqrt{8-y^{2}}\) that lies above the rectangle enclosed by the lines \(x=0,\) \(x=5,\) \(y=0,\) \( y=2\)

Question

The part of the surface \(z=\dfrac{2}{3}( x^{3/2}+y^{3/2})\) that lies above the triangle enclosed by the lines \( x=0\), \(y=0\), and \(2x+3y=6\)

Question

The part of the surface \(z=\dfrac{2}{3}(x^{3/2}+y^{3/2})\) that lies above the triangle enclosed by \(x=0\), \(y=0\), and \(3x+y=3\)

Question

The part of the paraboloid \(z=4-x^{2}-y^{2}\) that lies above the \(xy\)-plane

Question

The part of the cylinder \(z=\sqrt{a^{2}-x^{2}}\) that lies above the square defined by \(-\dfrac{1}{2}a\leq x\leq \dfrac{1}{2}a\) and \(-\dfrac{1 }{2}a\leq y\leq \dfrac{1}{2}a\), \(a\gt 0\)

Question

The part of the cone \(z=\sqrt{x^{2}+y^{2}}\) that lies inside the cylinder \(x^{2}+y^{2}=2x\)

Question

The part of the sphere \(x^{2}+y^{2}+z^{2}=4z\) that lies within the paraboloid \(x^{2}+y^{2}=2z\)

Question

The part of the surface \(z=xy\) in the first octant that lies within the cylinder \(x^{2}+y^{2}=a^{2}\), \(a\gt 0\)

Question

The part of the surface \(z=x^{2}-y^{2}\) in the first octant that lies within the cylinder \(x^{2}+y^{2}=4\)

Question

The part of the sphere \(x^2+y^{2}+z^{2}=4z\) that lies between the planes \(z=1\) and \(z=3\).

Question

The part of the sphere \(x^{2}+y^{2}+z^{2}=4a^{2}\) that lies inside the cylinder \(x^{2}+y^{2}=2ax\), \(a\gt 0\)

Question

Surface Area Find the surface area cut from the hyperbolic paraboloid \(y^{2}-x^{2}=6z\) by the cylinder \(x^{2}+y^{2}=36\).

Question

Surface Area Find the surface area of the part of \(z=4-y^{2}\) that lies in the first octant and is enclosed by \(z=0\), \(x=0\), \(x=y\), and \( y=2\).

Question

Surface Area Find the surface area of the part of \(x^{2}=y\) that lies in the first octant under the plane \(x+z=3\). (Hint: Project the surface onto the \(xz\)-plane.)

Question

Surface Area Find the surface area of the part of the paraboloid \(z=9-x^{2}-y^{2}\) that lies between the planes \(z=0\) and \(z=8\).

Question

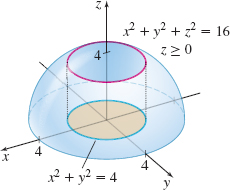
Surface Area Find the surface area of the part of the hemisphere \(x^{2}+y^{2}+z^{2}=16,\) \(z\geq 0,\) that lies inside the cylinder bounded by \(x^{2}+y^{2}=4.\) See the figure.

Question

Surface Area of the Pantheon The Pantheon in Rome is the largest unreinforced concrete dome in the world. Its inner surface is a hemisphere of diameter \(43.3 \text m\) with an open circular ocular \(9.1 \text m\) in diameter cut from its apex. Find the inner surface area of the dome.

Question

Surface Area

1. Graph the surface \(z=10e^{-( x^{2}+y^{2})}\) that lies inside the cylinder \(x^{2}+y^{2}=4\).
2. Find the surface area of the surface graphed in (a).

Question

Surface Area

1. Set up, but do not evaluate, the integral to find the surface area of the part of the surface \(z=1-x^{4}-y^{2} \) that lies above the \(2xy\)-plane.
2. Graph the surface.

Question

Derive the formula \(S=\pi a\sqrt{a^{2}+h^{2}}\) for the lateral surface area of a right circular cone of base radius \(a\) and altitude \(h\).

Question

Show that the area of the first-octant portion of the plane \( \dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\) (where \(a, b\), and \(c\) are positive) is \(S=\dfrac{1}{2}\sqrt{a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2}}\).

Question

Use a double integral to derive the formula for the surface area of a sphere of radius \(R\).

Question

Let \(F\) denote a function of three variables that possesses continuous first-order partial derivatives at each point of its domain. Suppose also that \(F_{z}(x,y,z)\) is never \(0\). If \(S\) is the area of the part of the surface \(F(x,y,z)=0\) that lies over the closed, bounded region \( R\), show that \[ \begin{array}{rcl} S=\int\limits\int_{\kern-11ptR}\dfrac{\sqrt{[F_{x}(x,y,z)]^{2}+[F_{y}(x,y,z)]^{2}+[F_{z}(x,y,z)]^{2}}}{|F_{z}(x,y,z)|}\,d\!A \end{array} \]

941

Question

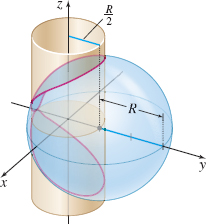
Surface Area The center of a sphere of radius \(R\) is on the surface of a right circular cylinder of base radius \(\dfrac{R}{2}\). Find the surface area of the sphere inside the cylinder. See the figure.

Question

For the plane surface \(F(x,y,z)=Ax+By+Cz-D=0\), \(C\neq 0\), if \( z=f(x,y)\), show that the surface area \(S=\displaystyle\iint\limits_{\kern-3ptR}\sqrt{ [f_{x}(x,y)]^{2}+[f_{y}(x,y)]^{2}+1}\,d\!A\) can be written as \[ S=\displaystyle\iint\limits_{\kern-3ptR}\sec \gamma \,d\!A \]

where \(\gamma \) is the positive acute angle between the normal \(\mathbf{n}=A \mathbf{i}+B\mathbf{j}+C\mathbf{k}\) to the plane and \(\mathbf{k}\).