14.6 The Triple Integral
OBJECTIVES
When you finish this section, you should be able to:
- Find a triple integral defined over a closed box (p. 942)
- Find a triple integral defined over a more general solid (p. 942)
- Find the volume of a solid (p. 944)
- Find the mass, center of mass, and moments of inertia of a solid (p. 944)
- Find a triple integral defined over \(xz\)-simple and \(yz\)-simple solids (p. 946)
Just as single integrals are used to integrate over closed intervals \([a, b]\), and double integrals are used to integrate over two-dimensional, closed, bounded regions \(R\), triple integrals are used to integrate over three-dimensional, closed, bounded solids \(E\). For example, we have seen that if \(\rho =\rho (x)\) is the mass density of a long thin wire, then the single integral \(\int_{a}^{b}\rho (x)\,{\it dx} \) models the mass of the wire from \(a\) to \(b.\) Also if \(\rho =\rho (x,y)\) is the mass density of a lamina, then the double integral \( \displaystyle\iint\limits_{\kern-3ptR}\rho (x,y)\, {\it dA}\) models the mass \(M\) of the lamina over \(R.\) Similarly, a triple integral can be used to find the mass of a solid with mass density \(\rho =\rho (x,y,z)\).
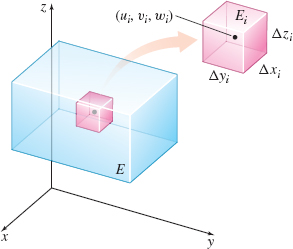
We begin with a function \(f\) of three variables defined over a box-shaped solid \(E\) in three-dimensional space. Partition \(E\) into \(n\) smaller rectangular boxes \(E_{1},E_{2},\ldots ,E_{i},\ldots , E_{n}\) by drawing planes parallel to the three coordinate planes, as shown in Figure 41.
The norm of the partition, denoted by \(\Vert P\Vert\), is defined as the length of the longest diagonal of the boxes \(E_{i}\). If \(\Delta x_{i}, \) \(\Delta y_{i}\), and \(\Delta z_{i}\) denote the length, width, and height, respectively, of the \(i\)th box, then its volume is \(\Delta V_{i}=\Delta x_{i}\Delta y_{i}\Delta z_{i}\). In each box \(E_{i}\), we arbitrarily select a point \((u_{i},v_{i},w_{i}),\) evaluate \(f(u_{i},v_{i},w_{i}),\) multiply \( f(u_{i},v_{i},w_{i})\) by \(\Delta V_{i},\) and form the sums \[ \sum_{i=1}^{n}f(u_{i},v_{i},w_{i})\Delta V_{i} \]
Sums of this form are referred to as Riemann sums of \(f\) for the partition \(P\). If \(\lim\limits_{\left\Vert P\right\Vert \rightarrow 0}\sum\limits_{i=1}^{n}f(u_{i},v_{i},w_{i})\Delta V_{i}\) exists and does not depend on the choice of the partition or on the choice of \( (u_{i},v_{i},w_{i})\), then this limit is called the triple integral of \(f\) over \(E\).
spanDEFINITIONspan Triple Integral
Let \(f\) be a function of three variables defined over a closed, bounded, box-shaped solid \(E\). The triple integral of \(f\) over \(E\) is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{ \displaystyle\iiint\limits_{\kern-3ptE}f(x,y,z)\,{\it dV}=\lim\limits_{\Vert P\Vert \rightarrow 0}\sum\limits_{i=1}^{n}f(u_{i},v_{i},w_{i})\Delta V_{i} } \]
provided the limit exists.
942
As with single integrals and double integrals, it can be shown that if \(f\) is continuous on \(E,\) then \(\iiint\limits_{\kern-2ptE}f(x,y,z)\,{\it dV}\) exists.
There are six variations for the triple integral of \(f\) over \(E.\) They are \[ \begin{array} \displaystyle\iiint\limits_{\kern-3ptE}f(x,y,z)\,{\it dx}\,{\it dy}\,{\it dz} \displaystyle\iiint\limits_{\kern-3ptE}f(x,y,z)\,{\it dx}\,{\it dz}\,{\it dy} \displaystyle\iiint\limits_{\kern-3ptE}f(x,y,z)\,{\it dy}\,{\it dx}\,{\it dz} \\ \displaystyle\iiint\limits_{\kern-3ptE}f(x,y,z)\,{\it dy}\,{\it dz}\,{\it dx} \displaystyle\iiint\limits_{\kern-3ptE}f(x,y,z)\,{\it dz}\,{\it dx}\,{\it dy} \displaystyle\iiint\limits_{\kern-3ptE}f(x,y,z)\,{\it dz}\,{\it dy}\,{\it dx} \end{array} \]
Fubini’s Theorem for triple integrals uses three iterated integrals to find \( \iiint\limits_{\kern-3ptE}f(x,y,z)\,{\it dV}\).
THEOREM Fubini’s Theorem for Triple Integrals
Let \(f\) be a function of three variables defined over the closed box \( E,\) where \(x_{1}\leq x\leq x_{2}\), \(y_{1}\leq y\leq y_{2}\), and \(z_{1}\leq z\leq z_{2}\). If \(f\) is continuous on \(E\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{ \displaystyle\iiint\limits_{\kern-3ptE}f(x,y,z) \,{\it dV}=\int_{x_{1}}^{x_{2}}\left\{ \int_{y_{1}}^{y_{2}}\left[ \int_{z_{1}}^{z_{2}}f(x,y,z)\,{\it dz}\right] {\it dy}\right\} {\it dx} } \]
The iterated integral on the right is shown first with respect to \(z\), then \( y\), and finally \(x\). However, the same result is obtained no matter what order is used. To find \(\int_{z_{1}}^{z_{2}}f(x,y,z)\,{\it dz}\), we treat \(x\) and \(y\) as constants and integrate partially with respect to \(z\). As is the case with iterated double integrals, the braces and brackets are usually omitted.
1 Find a Triple Integral Defined over a Closed Box

Finding a Triple Integral Defined over a Closed Box
Find \(\iiint\limits_{\kern-3ptE}4xyz\,{dV}\) if \(E\) is the closed box \(0\leq x\leq 1\), \(0\leq y\leq 2\), and \(0\leq z\leq 3\) shown in Figure 42.
Solution Since \(f(x,y,z) =4xyz\) is continuous on \(E,\) we use Fubini’s Theorem for triple integrals. \[ \begin{eqnarray*} \displaystyle\iiint\limits_{\kern-3ptE}4xyz\,{\it dV} &=&\int_{0}^{1}\int_{0}^{2}\int_{0}^{3}4xyz\,{\it dz}\,{\it dy}\,{\it dx}=\int_{0}^{1} \int_{0}^{2}4xy\left[ \frac{z^{2}}{2}\right] _{0}^{3}\,{\it dy}\,{\it dx}\\ &=&\int_{0}^{1}\int_{0}^{2}18xy\,{\it dy}\,{\it dx}=\int_{0}^{1}18x\left[ \frac{y^{2}}{2}\right]_{0}^{2}\,{\it dx} \notag \\ &=&\int_{0}^{1}36x\,{\it dx}=\big[ 18x^{2}\big] _{0}^{1}=18 \end{eqnarray*} \]
NOW WORK
Problem 9.
2 Find a Triple Integral Defined over a More General Solid
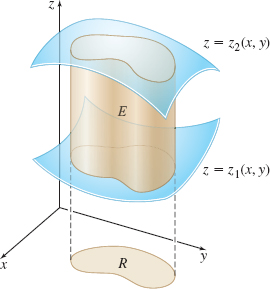
Consider a solid \(E\) in space enclosed on the top by a surface \( z=z_{2}(x,y)\) and on the bottom by a surface \(z=z_{1}(x,y)\), where \( z_{1}\leq z_{2}\) and the functions \(z_{1}\) and \(z_{2}\) are continuous. The sides of \(E\) are a cylinder whose intersection with the \(xy\)-plane forms a closed, bounded region \(R.\) See Figure 43. Since the projection of \(E\) onto the \(xy\)-plane results in a closed, bounded region \(R,\) and \(E\) lies between the two surfaces \(z_{1}\) and \(z_{2}\), the solid \(E\) is called xy-simple. The next theorem, which we do not prove, provides a way to find triple integrals defined over solids that are \(xy\)-simple.
943
THEOREM Triple Integral over an \(xy\)-Simple Solid
Let \(E\) be an \(xy\)-simple solid that lies between the two surfaces \(z=z_{1}(x, y)\) and \(z=z_{2}(x, y)\), where \(z_{1}\leq z_{2}\), and whose projection onto the \(xy\)-plane is a closed, bounded region \(R\). If \(f\) is a function of three variables that is continuous on \(E\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{ \int\limits\int\limits\int\limits_{\kern-11ptE}f(x,y,z)\,{\it dV}=\int\limits\int\limits_{\kern-8ptR} \left[ \int_{z_{1}(x, y)}^{z_{2}(x, y)}f(x, y, z)\,{\it dz}\right] {\it dA} } \]
If the region \(R\) is \(x\)-simple, and \(R\) is enclosed by \(y=y_{1}(x) ,\) \(y=y_{2}(x) ,\) \(y_{1}\leq y_{2},\) \(a\leq x\leq b,\) then \begin{eqnarray*} \iiint\limits_{\kern-2ptE}f(x, y,z)\,{\it dV}&=&\iint\limits_{\kern-2ptR}\left[ \int_{z_{1}(x, y)}^{z_{2}(x, y)}f(x, y,z)\,{\it dz}\right] {\it dA}\\[4pt] &=&\int_{a}^{b}\int_{y_{1}(x)}^{y_{2}(x)}\int_{z_{1}(x, y)}^{z_{2}(x, y)}f(x, y,z)\,{\it dz}\,{\it dy}\,{\it dx} \end{eqnarray*}
If the region \(R\) is \(y\)-simple, and \(R\) is enclosed by \(x=x_{1}(y) ,\) \(x=x_{2}(y) ,\) \(x_{1}\leq x_{2},\) \(c\leq y\leq d,\) then \begin{eqnarray*} \iiint\limits_{\kern-2ptE}f(x, y,z)\,{\it dV}&=&\iint\limits_{\kern-2ptR}\left[ \int_{z_{1}(x, y)}^{z_{2}(x, y)}f(x, y, z)\,{\it dz}\right] {\it dA}\\[4pt] &=&\int_{c}^{d}\int_{x_{1}(y)}^{x_{2}(y)}\int_{z_{1}(x, y)}^{z_{2}(x, y)}f(x, y,z)\,{\it dz}\,{\it dx}\,{\it dy} \end{eqnarray*}

Finding a Triple Integral Defined over an \(xy\)-Simple Solid
Find the triple integral \(\iiint\limits_{\kern-2ptE}4x\,{\it dV}\) over the tetrahedron formed by the coordinate planes and the plane \(2x+3y+4z=12\).
Solution The solid \(E\) is shown in Figure 44(a). A typical plane section of \(E\) using a plane perpendicular to the \(x\)-axis reveals that the upper surface is \(z=z_{2}(x, y)=\dfrac{1}{4}(12-2x-3y)\) and the lower surface is \(z=z_{1}(x, y)=0\). So, \(E\) is \(xy\)-simple. The region \(R\) in the \(xy\)-plane is the triangle enclosed by the \(x\)-axis, the \(y\)-axis, and the line \(y=\dfrac{1}{3}(12-2x)=4-\dfrac{2x}{3}\), as shown in Figure 44(b). The triangle \(R\) is both \(x\)-simple and \(y\)-simple. If we treat it as an \(x\)-simple region, so that \(R\) is given by \(y=0\), \(y=4-\dfrac{2x}{3}\) and \(\leq x\leq 6\), we have \begin{eqnarray*} \iiint\limits_{\kern-2ptE}4x\,{\it dV}&=&\int_{a}^{b}\int_{y_{1}(x)}^{y_{2}(x)} \int_{z_{1}(x, y)}^{z_{2}(x, y)}4x\,{\it dz}\,{\it dy}\,{\it dx}\\ &=&\int_{0}^{6}\int_{0}^{4-2x/3}\int_{0}^{(1/4)(12-2x-3y)}4x\,{\it dz}\,{\it dy}\,{\it dx} \notag \\ &=&\int_{0}^{6}\int_{0}^{4-2x/3} 4x \big[z\big] _{0}^{( 1/4) (12-2x-3y)}\,{\it dy}\,{\it dx}=\int_{0}^{6}\int_{0}^{4-2x/3}~4x\!\left( \dfrac{12-2x-3y}{4 }\right) {\it dy}\,{\it dx} \notag\\ &=&\int_{0}^{6}\int_{0}^{4-2x/3}(12x-2x^{2}-3xy)\,{\it dy}\,{\it dx}=\int_{0}^{6}\left[ ( 12x-2x^{2}) \,y-3x\dfrac{y^{2}}{2}\,\right] _{0}^{4-2x/3}{\it dx} \notag\\ & =&\int_{0}^{6}\left( 24x-8x^{2}+\dfrac{2}{3}x^{3}\right) {\it dx}=\left[ 12x^{2}- \dfrac{8}{3}x^{3}+\dfrac{1}{6}x^{4}\right] _{0}^{6}=72 \end{eqnarray*}
NOW WORK
Problems 11 and 21.
3 Find the Volume of a Solid
944
If \(z=f(x, y) =1\) on \(R,\) the double integral \(\iint\limits_{\kern-1ptR}f(x, y) \, {\it dA}= \iint\limits_{\kern-1ptR}{\it dA}\) is numerically equal to the area of the region \(R.\) If \(f(x, y,z)=1\) on \(E\), then the triple integral \(\iiint\limits_{\kern-1ptE}f(x, y,z)\,{\it dV}=\iiint\limits_{\kern-1ptE}{\it dV}\) equals (numerically) the volume of the solid \(E\). That is, \[\bbox[5px, border:1px solid black, #F9F7ED]{ \hbox{Volume \(V\) of a solid \(E\):}\quad V=\iiint\limits_{\kern-1ptE}\,{\it dV} } \]
Finding the Volume of a Solid
Find the volume \(V\) of the solid \(E\) in the first octant that is enclosed by the paraboloid \(z=16-4x^{2}-y^{2}\) and the \(xy\)-plane.
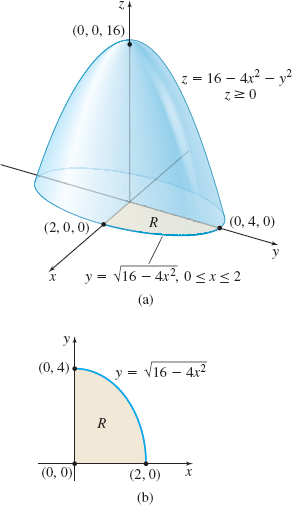
Solution Figure 45(a) shows the solid \(E\), which is \(xy\)-simple. The upper surface is the paraboloid \(z=z_{2}(x, y)=16-4x^{2}-y^{2}\) and the lower surface is the plane \(z=z_{1}(x, y)=0\). The region \(R\) in the \(xy\)-plane is enclosed by the \(x\)-axis, the \(y\)-axis, and part of the ellipse \(4x^{2}+y^{2}=16,\) \(x\geq 0,\) \(y\geq 0.\)The region \(R\) is both \(x\)-simple and \(y\)-simple. We choose to use the iterated integral for an \(x\)-simple region, so that \(0\leq y\leq \sqrt{16-4x^{2}}\) and \(0\leq x\leq 2.\) See Figure 45(b). The volume \(V\) of \(E\) is given by \begin{eqnarray*} V&=&\iiint\limits_{\kern-2ptE}\,{\it dV}=\int_{a}^{b}\int_{y_{1}(x)}^{y_{2}(x)} \int_{z_{1}(x, y)}^{z_{2}(x, y)}{\it dz}\, {\it dy}\,{\it dx}= \int_{0}^{2} \int_{0}^{\sqrt{16-4x^{2}} } \int_{0}^{16-4x^{2}-y^{2}}{\it dz}\, {\it dy}\,{\it dx} \\[4pt] &=&\int_{0}^{2}\int_{0}^{\sqrt{16-4x^{2}}}( 16-4x^{2}-y^{2}) \,{\it dy}\,{\it dx}=\int_{0}^{2}\left[ (16-4x^{2})y-\dfrac{y^{3}}{3}\right] _{0}^{\sqrt{ 16-4x^{2}}}\,{\it dx} \\[4pt] &=&\int_{0}^{2}\!\left( (16-4x^2)^{3/2} -\dfrac{( 16-4x^{2}) ^{3/2}}{3}\right)\!{\it dx} = \dfrac{16}{3}\int^2_0 (4-x^2)^{3/2}\,{\it dx} \end{eqnarray*}
We use the Table of Integrals, Integral 69 with \(a=2\). Then \begin{eqnarray*} V=\dfrac{16}{3}\int^2_0 (4-x^2)^{3/2}\,{\it dx} &=&\dfrac{16}{3}\left[ \dfrac{x}{4} ( 4-x^{2}) ^{3/2}+\dfrac{3x}{2 }\sqrt{4-x^{2}}+6\sin ^{-1}\dfrac{x}{2}\right] _{0}^{2}\\[4pt] &=& \dfrac{16}{3} (6) \left(\dfrac{\pi}{2}\right)=16\pi \end{eqnarray*}
NOTE
Alternatively, we could use a CAS to find the integral or we could use the trigonometric substitution \(x=2\sin\theta\), \(-\dfrac{\pi}{2}\leq \theta\leq \dfrac{\pi}{2} \).
NOW WORK
Problem 35.
4 Find the Mass, Center of Mass, and Moments of Inertia of a Solid
Triple integrals can be used to find the mass, center of mass, and moments of inertia of solids. The formulas are obtained in a manner similar to those using double integrals, so we only state them here.
The mass \(M\) of a solid \(E\) of volume \(V\) with mass density \(\rho =\rho (x, y, z)\) that is continuous in \(E\) is given by \[\bbox[5px, border:1px solid black, #F9F7ED]{ M=\iiint\limits_{\kern-2ptE}\rho (x, y,z) \,{\it dV} } \]
The moments of the solid about the coordinate planes are \[\bbox[5px, border:1px solid black, #F9F7ED]{ M_{xy}=\iiint\limits_{\kern-2ptE}z\rho (x, y,z)\,{\it dV}\qquad M_{xz}=\iiint\limits_{\kern-2ptE}y\rho (x, y,z)\,{\it dV}\qquad M_{yz}=\iiint\limits_{\kern-2ptE}x \rho (x, y, z)\,{\it dV} } \]
945
The center of mass of the solid is the point \((\bar{x}, \bar{y}, \bar{z})\) whose coordinates are given by \[\bbox[5px, border:1px solid black, #F9F7ED]{ \bar{x}=\dfrac{M_{yz}}{M}=\dfrac{\iiint\limits_{\kern-2ptE}x\rho (x, y,z) \,{\it dV}}{\iiint\limits_{\kern-2ptE}\rho (x, y,z) \,{\it dV}} \qquad \bar{y}=\dfrac{M_{xz}}{M}=\dfrac{\iiint\limits_{\kern-2ptE}y\rho (x, y,z) \,{\it dV}}{\iiint\limits_{\kern-2ptE}\rho (x, y,z) \,{\it dV}} \qquad \bar{z}=\dfrac{M_{xy}}{M}=\dfrac{\iiint\limits_{\kern-2ptE}z\rho (x, y,z) \,{\it dV}}{\iiint\limits_{\kern-2ptE}\rho (x, y,z) \,{\it dV}} } \]
The moment of inertia about an axis \(a\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{ I_{a}=\iiint\limits_{\kern-2ptE}r^{2}\rho (x, y, z)~ {\it dV} } \]
where \(r\) is the distance from the point \((x, y, z)\) of the solid to the axis \(a\) about which the moment is to be found.
Finding the Mass and Center of Mass of a Solid
 Find the mass \(M\) of a solid in the shape of a tetrahedron cut from the first octant by the plane \(x+y+z=1\) if the mass density \(\rho =\rho (x, y, z) \) is proportional to the distance from the \(yz\)-plane.
Find the mass \(M\) of a solid in the shape of a tetrahedron cut from the first octant by the plane \(x+y+z=1\) if the mass density \(\rho =\rho (x, y, z) \) is proportional to the distance from the \(yz\)-plane.- Find the center of mass \((\bar{x}, \bar{y}, \bar{z})\) of the tetrahedron.
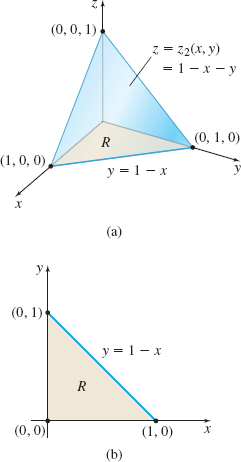
Solution Figure 46(a) shows the solid \(E\) that is \(xy\)-simple. It is enclosed by the surfaces \(z=z_{1}(x, y)=0\) and \(z=z_{2}(x, y)=1-x-y\), and its projection onto the \(xy\)-plane is the closed, bounded \(x\)-simple region \(R\) defined by the lines \(y=0\) and \(y=1-x,\) where \(0\leq x\leq 1\). See Figure 46(b).
(a) Since the mass density \(\rho =\rho (x, y,z) \) is proportional to the distance from the \(yz\)-plane, we have \(\rho (x, y,z) =kx,\) where \(k\) is the constant of proportionality. Then the mass \(M\) is \[ M=\iiint\limits_{\kern-2ptE}\rho (x, y, z) \,{\it dV}=\iiint\limits_{\kern-2ptE}kx\,{\it dV}=k\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-x-y}x \,{\it dz}\,{\it dy}\,{\it dx} \]
Using a CAS, \(M=\dfrac{k}{24}.\)
(b) The center of mass \((\bar{x}, \bar{y}, \bar{z})\) is \begin{eqnarray*} \bar{x}&=&\dfrac{\iiint\limits_{\kern-2ptE}x\rho ( x, y,z) \,{\it dV}}{M}=\dfrac{ \iiint\limits_{\kern-2ptE}xkx\,{\it dV}}{\dfrac{k}{24}}=24\iiint\limits_{\kern-2ptE}x^{2}\,{\it dV}\\[7pt] &=&24\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-x-y}x^{2}\,{\it dz}\,{\it dy}\,{\it dx} \end{eqnarray*}
Using a CAS, \(\overline{x}=\dfrac{2}{5}.\) \begin{equation*} \bar{y}=\dfrac{\iiint\limits_{\kern-2ptE}y\rho (x, y,z) \,{\it dV}}{M}=\dfrac{ \iiint\limits_{\kern-2ptE}ykx\,{\it dV}}{\dfrac{k}{24}}=24\int_{0}^{1}\int_{0}^{1-x} \int_{0}^{1-x-y}{\it xy}\,{\it dz}\,{\it dy}\,{\it dx} \end{equation*}
Using a CAS, \(\bar{y}=\) \(\dfrac{1}{5}.\)
946
\begin{equation*} \bar{z}=\dfrac{\iiint\limits_{\kern-2ptE}z\rho (x, y,z) \,{\it dV}}{M}=\dfrac{ \iiint\limits_{\kern-2ptE}zkx\,{\it dV}}{\dfrac{k}{24}}=24\int_{0}^{1}\int_{0}^{1-x} \int_{0}^{1-x-y}xz\,{\it dz}\,{\it dy}\,{\it dx} \end{equation*}
Using a CAS \(\ \bar{z}=\) \(\dfrac{1}{5}.\)
The center of mass of the tetrahedron is located at the point \(\left( \dfrac{2}{5},\dfrac{1}{5},\dfrac{1}{5}\right).\)
NOTE
The integrals in (a) and (b) can be found by hand, but the integration is somewhat tedious.
NOW WORK
Problem 43.
Finding the Moment of Inertia About the \(z\)-axis of a Solid
Find the moment of inertia about the \(z\)-axis of the homogeneous solid of mass density \(\rho \) in the first octant enclosed by the surface \(z=4xy\) and the planes \(z=0\), \(x=3\), and \(y=2\).
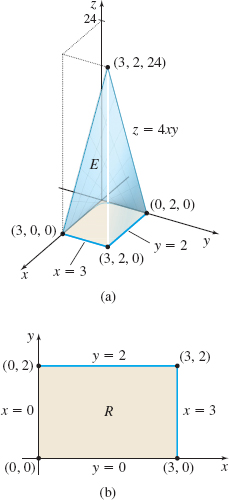
Solution The moment of inertia about the \(z\)-axis is \[ I_{z}=\iiint\limits_{\kern-2ptE}r^{2}\rho \,{\it dV} \]
where \(r=\sqrt{x^{2}+y^{2}}\) is the distance of the point \((x, y, z) \) from the \(z\)-axis.
Figure 47(a) shows the solid \(E\), which is \(xy\)-simple. The upper surface is \(z=z_{2}(x, y)=4xy\) and the lower surface is the plane \(z=z_{1}(x, y)=0\). The region \(R\) in the \(xy\)-plane is enclosed by the \(x\)-axis, the \(y\)-axis, the line \(x=3\), and the line \(y=2\), as shown in Figure 47(b). The region \(R\) is both \(x\)-simple and \(y\)-simple. \begin{eqnarray*} I_{z} &=&\iiint\limits_{\kern-2ptE}(x^{2}+y^{2})\rho \,{\it dV}=\rho \int_{0}^{3}\int_{0}^{2}\int_{0}^{4xy}(x^{2}+y^{2})\,{\it dz}\,{\it dy}\,{\it dx} \notag \\[4pt] &=&\rho \int_{0}^{3}\int_{0}^{2}\big[ z(x^{2}+y^{2})\big] _{0}^{4xy}\,{\it dy}\,{\it dx}=\rho \int_{0}^{3}\int_{0}^{2}( 4x^{3}y+4xy^{3}) \,{\it dy}\,{\it dx}\\[4pt] &=&\rho \int_{0}^{3}\big[ 2x^{3}y^{2}+xy^{4}\big] _{0}^{2}\,\,{\it dx} \notag \\[4pt] &=&\rho \int_{0}^{3}( 8x^{3}+16x) \,{\it dx}=\rho \big[ 2x^{4}+8x^{2}\big] _{0}^{3}=\rho ( 162+72) =234\rho \end{eqnarray*}
NOW WORK
Problem 47.
5 Find a Triple Integral Defined over \(xz\)-Simple and \(yz\)-Simple Solids

Triple integrals on certain types of regions in space are best found by integrating first with respect to \(x\) or \(y\) rather than \(z\).
Suppose a solid \(E\) in space is enclosed by the two surfaces \(y=y_{1}(x, z)\) and \(y=y_{2}(x, z)\), where the functions \(y_{1},\) and \(y_{2}\) are continuous and \(y_{1}\leq y_{2}.\) If the projection of \(E\) onto the \(xz\)-plane is a closed, bounded region \(R\), then \(E\) is called an xz-simple solid. See Figure 48.
947
THEOREM Triple Integral over an \(xz\)-Simple Solid
If \(f\) is a function of three variables that is continuous on an \(xz\)-simple solid \(E\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{ \iiint\limits_{\kern-2ptE}f(x, y, z)\,{\it dV}=\iint\limits_{\kern-2ptR}\left[ \int_{y_{1}(x, z)}^{y_{2}(x, z)}f(x, y, z)\,{\it dy}\right]\! {\it dA} } \]
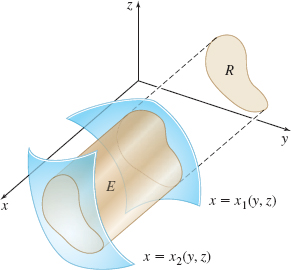
Similarly, suppose a solid \(E\) in space is enclosed by the two surfaces \(x=x_{1}(y,z)\) and \(x=x_{2}(y,z)\), where the functions \(x_{1}\) and \(x_{2}\) are continuous and \(x_{1}\leq x_{2}.\) If the projection of \(E\) onto the \(yz\)-plane is a closed, bounded region \(R\), then \(E\) is called a yz-simple solid. See Figure 49.
THEOREM Triple Integral over an \(yz\)-Simple Solid
If \(f\) is a function of three variables that is continuous on a \(yz\)-simple solid \(E\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{ \iiint\limits_{\kern-2ptE}f(x, y, z)\,{\it dV}=\iint\limits_{\kern-2ptR}\left[ \int_{x_{1}(y, z)}^{x_{2}(y, z)}f(x, y, z)\,{\it dx}\right]\! {\it dA} } \]
Finding the Volume of a Solid That Is \(yz\)-simple
Find the volume \(V\) of the solid \(E\) that is enclosed by the cylinder \(y^{2}+z^{2}=4,\) and the planes \(x=0,\) \(z=0,\) and \(x+z=5.\)
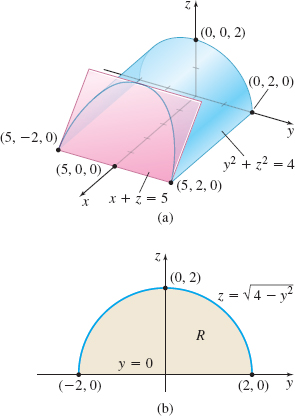
Solution Figure 50(a) shows that the solid \(E\) is \(yz\)-simple. The front surface is the plane \(x_{2}(y, z) =5-z\) and the back surface is the plane \(x_{1}(y, z) =0.\) The region \(R\) in the \(yz\)-plane is enclosed by the \(y\)-axis and the semi-circle \(z=\sqrt{4-y^{2}};\) it is \(y\)-simple. So, \(0\leq z\leq \sqrt{4-y^{2}}\) and \(-2\leq y\leq 2.\) See Figure 50(b). The volume \(V\) of \(E\) is given by \begin{eqnarray*} V &=&\iiint\limits_{\kern-2ptE}\,{\it dV}=\iint\limits_{\kern-2ptR}\left[ \int_{x_{1}(y,z)}^{x_{2}(y,z)}{\it dx}\right] {\it dz}\,{\it dy}=\int_{-2}^{2}\int_{0}^{ \sqrt{4-y^{2}}}\int_{0}^{5-z}{\it dx}\,{\it dz}\,{\it dy}\\[4pt] &=&\int_{-2}^{2}\int_{0}^{\sqrt{4-y^{2}} }( 5-z) \,{\it dz}\,{\it dy} =\int_{-2}^{2}\left[ 5z-\dfrac{z^{2}}{2}\right] _{0}^{\sqrt{4-y^{2}}}\,{\it dy}\\[4pt] &=&\int_{-2}^{2}\left( 5\sqrt{4-y^{2}}-\dfrac{4-y^{2}}{2}\right){\it dy}\\[4pt] &=&5\int_{-2}^{2}\sqrt{4-y^{2}}\, {\it dy}-\int_{-2}^{2}\left( 2-\dfrac{y^{2}}{2} \right) {\it dy} \notag \\[4pt] &=&5(2\pi) -\left[ 2y-\dfrac{y^{3}}{6}\right] _{-2}^{2}=10\pi -\dfrac{16}{3} \end{eqnarray*}
NOTE
\(\int_{-2}^{2}\sqrt{4-y^{2}} {\it dy}\) equals the area of a semi-circle of radius \(2,\) namely \(2\pi .\)
NOW WORK
Example 2 treating \(E\) as an \({xz}\)-simple region.