14.7 Triple Integrals Using Cylindrical Coordinates
950
OBJECTIVES
When you finish this section, you should be able to:
- Convert rectangular coordinates to cylindrical coordinates (p. 950)
- Find a triple integral using cylindrical coordinates (p. 951)
We have seen that there are instances where it is easier to find a double integral using polar coordinates than to find it using rectangular coordinates. For triple integrals, we give two alternatives to integration in rectangular coordinates: One uses cylindrical coordinates and the other uses spherical coordinates (Section 14.8).
1 Convert Rectangular Coordinates to Cylindrical Coordinates
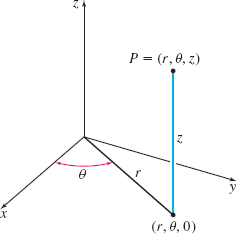
If the rectangular coordinates of a point \(P\) in three-dimensional space are \((x, y, z)\) and if \((r,\theta, 0) \) are the polar coordinates for the projection of \(P\) onto the \(xy\)-plane, then the point \(P\) can be located by the ordered triple \((r,\theta ,z),\) called the cylindrical coordinates of the point \(P\).
Figure 51 shows how to graph a point \(P=(r,\theta ,z) \). The algebraic relationship between the cylindrical coordinates \((r,\theta ,z)\) and the rectangular coordinates \((x, y, z)\) of a point \(P\) is given by the formulas \[\bbox[5px, border:1px solid black, #F9F7ED] { \begin{array}{lll} x=r\cos \theta \qquad y=r\sin \theta \qquad z=z \end{array} } \]
Converting Between Cylindrical Coordinates and Rectangular Coordinates
- Find the rectangular coordinates of a point \(P\) whose cylindrical coordinates are \(\left( 6,\dfrac{\pi }{3},-2\right) \).
- Find the cylindrical coordinates of a point \(P\) whose rectangular coordinates are (\(\sqrt{3},1, 5\)).
Solution (a) We use the equations \(x=r\cos \theta \) and \(y=r\sin \theta \) with \(r=6\) and \(\theta =\dfrac{\pi }{3}.\) Then \begin{equation*} x=6\cos \dfrac{\pi }{3}=3 \qquad y=6\sin \dfrac{\pi }{3}=3\sqrt{3} \qquad z=-2 \end{equation*}
In rectangular coordinates, \(P=( 3, 3\sqrt{3},-2)\).
(b) In cylindrical coordinates \(r=\sqrt{x^2+y^2} =\sqrt{3+1}=2\). Then \(\cos\theta=\dfrac{x}{r} =\dfrac{\sqrt{3}}{2}\) and \(\sin \theta=\dfrac{y}{r}=\dfrac{1}{2}\) so \(\theta=\dfrac{\pi}{6}\). Since \(z\) remains the same, the point \(P\) in cylindrical coordinates is \((r,\theta,z) = \left(2,\dfrac{\pi}{6},5\right)\).
NOW WORK
Problems 5 and 13.
NOTE
The numbers \(r, \theta\), and \(z\) are called cylindrical coordinates because if \(r\) is a constant, then the surface traced out by the set of points \((r,\theta ,z)\) is a cylinder.
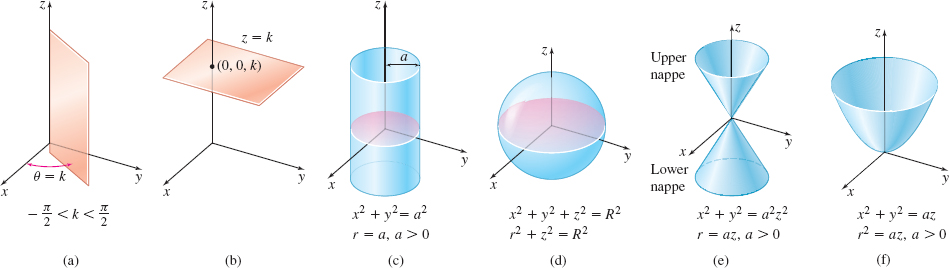
Table 1 lists the equations of several surfaces expressed in rectangular coordinates and in cylindrical coordinates. Figure 52 illustrates the surfaces.
| Surface | Rectangular | Cylindrical |
|---|---|---|
| (a) Half-Plane | \(y=x\tan k\) | \(\theta =k,\quad\) \(-\dfrac{\pi }{2}\lt k\lt\dfrac{\pi }{2}\) |
| (b) Plane | \(z=k\) | \(z=k\) |
| (c) Cylinder | \(x^{2}+y^{2}=a^{2}\) | \(r=a,\quad\) \(a\gt0\) |
| (d) Sphere | \(x^{2}+y^{2}+z^{2}=R^{2}\) | \(r^{2}+z^{2}=R^{2}\) |
| (e) Circular cone | \(x^{2}+y^{2}=a^{2}z^{2}\) | \(r=az,\quad a\gt 0\) |
| (f) Circular paraboloid | \(x^{2}+y^{2}=az\) | \(r^{2}=az,\quad\) \(a\gt0\) |
951
Triple integrals that have symmetry about an axis, particularly integrals involving cylinders or cones whose axes are aligned with the \(z\)-axis, are often easier to find using cylindrical coordinates.
2 Find a Triple Integral Using Cylindrical Coordinates
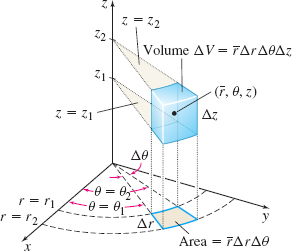
Consider a wedge-shaped solid enclosed by two planes passing through the \(z\) -axis (\(\theta =\theta _{1}\) and \(\theta =\theta _{2}\)), two concentric circular cylinders centered about the \(z\)-axis (\(r=r_{1}\) and \(r=r_{2}\)), and two parallel planes perpendicular to the \(z\)-axis (\(z=z_{1}\) and \(z=z_{2} \)), as shown in Figure 53. The projection of the wedge-shaped solid onto the xy-plane is a polar subregion whose area \(\Delta A\) is \begin{eqnarray*} \Delta A &=&\hbox{ outer sector }-\hbox{ inner sector}=\dfrac{1}{2} r_{2}^{2}\Delta \theta -\dfrac{1}{2}r_{1}^2\Delta \theta \\[1pt] &=&\dfrac{1}{2}\big( r_{2}^{2}\,-r_{1}^{2}\big) \Delta \theta = \dfrac{1}{2}( r_{2}+r_{1}) ( r_{2}-r_{1}) \Delta \theta =\overline{r}\Delta r\Delta \theta \end{eqnarray*}
where \(\bar{r}=\dfrac{r_{1}+r_{2}}{2},\) \(\Delta r=r_{2}-r_{1},\) and \(\Delta \theta =\theta _{2}-\theta _{1}\). The volume \(\Delta V\) of the wedge is \( \Delta V=\Delta A\Delta z=\bar{r}\Delta r\Delta \theta \Delta z.\) The differential \({\it dV}\) of volume \(V\) in cylindrical coordinates is \[\bbox[5px, border:1px solid black, #F9F7ED] { \begin{array}{lll} dV=r\,{\it dr}\,d\theta \, {\it dz} \end{array} } \]
NEED TO REVIEW?
The area of a sector of a circle is discussed in Appendix A.4, p. A-27.
Now consider a solid \(E.\) We partition \(E\) into wedge-shaped subsolids by passing planes and cylinders through \(E.\) After discarding all subsolids that do not lie entirely in \(E\), there will be \(n\) subsolids remaining. The shaded portion of Figure 54 illustrates a typical subsolid, denoted by \(E_{i}\). The norm \(\Vert P\Vert\) of the partition is the length of the longest diagonal of the largest subsolid.
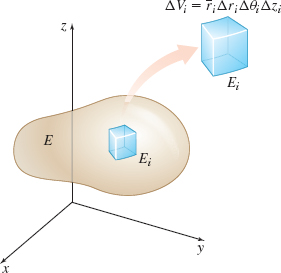
Now suppose \(f\) is a function of the cylindrical coordinates \(r,\theta \), and \(z\). Let \((\bar{r}_{i},\bar{\theta}_{i},\bar{z}_{i})\) be the center of \( E_{i},\) and evaluate \(f (\bar{r}_{i},\bar{\theta}_{i},\bar{z}_{i})\). Then form the sums \[ \sum_{i=1}^{n}f(\bar{r}_{i},\bar{\theta}_{i},\bar{z}_{i})\bar{r}_{i}\Delta r_{i}\Delta \theta _{i}\Delta z_{i} \]
It can be shown that if \(f\) is continuous on \(E\), then these sums have a limit as the norm \(\Vert P \Vert\) approaches 0. We define the triple integral as this limit. \[ \iiint\limits_{\kern-3ptE}f(r,\theta ,z)\,{\it dV}=\lim\limits_{\left\Vert P\right\Vert \rightarrow 0}\sum_{i=1}^{n}f(\bar{r} _{i},\bar{\theta}_{i},\bar{z}_{i})\bar{r}_{i}\Delta r_{i}\Delta \theta _{i}\Delta z_{i} \]
That is, \[\bbox[5px, border:1px solid black, #F9F7ED] { \begin{array}{lll} \displaystyle\iiint\limits_{\kern-3ptE}f(r,\theta ,z)\,{\it dV}=\displaystyle\iiint\limits_{\kern-3ptE}f(r,\theta ,z)~r\,{\it dr}\,d\theta \,{\it dz} \end{array} } \]
Sometimes a triple integral can be found using an iterated integral.
952
THEOREM Sufficient Condition for Using an Iterated Integral
Suppose a solid \(E\) is enclosed by the surfaces \(z=z_{1}(r,\theta )\) and \(z=z_{2}(r,\theta )\), where the functions \(z_{1}\) and \(z_{2}\) are continuous and \(0\leq z_{1}\leq z_{2}\). Suppose the projection of \(E\) onto the \(r\theta \)-plane is a closed, bounded region \(R\). If the function \(f\) of three variables is continuous on \(E\), then \[\bbox[5px, border:1px solid black, #F9F7ED] { \begin{array}{lll} \displaystyle\iiint\limits_{\kern-3ptE}f(r,\theta ,z)\,{\it dV}=\displaystyle\iint\limits_{\kern-3ptR} \left[ \int_{z_{1}(r,\theta )}^{z_{2}(r,\theta )}f(r,\theta ,z)\,{\it dz}\right] r\,dr\,d\theta \end{array} } \]
NOTE
The integrand contains a factor of \(r\) because in cylindrical coordinates the differential \({\it dV}\) of volume is \({\it dV}=r\,dr\,d\theta \,{\it dz}.\)
To find the value of the inside integral \(\int_{z_{1}(r,\theta )}^{z_{2}(r,\theta )}f(r,\theta ,z)\,{\it dz},\) we treat \(r\) and \(\theta \) as constants and integrate partially with respect to \(z\).
Suppose the region \(R\) is enclosed by the rays \(\theta =\theta _{1}\) and \( \theta =\theta _{2}\), and the curves \(r=r_{1}(\theta )\) and \(r=r_{2}(\theta ) \), where \(0\leq r_{1}\leq r_{2}.\) If the functions \(r_{1}\) and \(r_{2}\) are continuous for \(\theta _{1}\leq \theta \leq \theta _{2}\), then \[\bbox[5px, border:1px solid black, #F9F7ED] { \begin{array}{lll} \displaystyle\iiint\limits_{\kern-3ptE}f(r,\theta ,z)\,dV= \displaystyle\iiint\limits_{\kern-3ptE}f(r,\theta ,z)\,r\,dr\,d\theta \,{\it dz}=\int_{\theta_1 }^{\theta_2 }\left\{ \int_{r_{1}(\theta )}^{r_{2}(\theta )} \left[ \int_{z_{1}(r,\theta )}^{z_{2}(r,\theta )}f(r,\theta ,z)\,{\it dz}\right]\! r\,dr\right\} d\theta \end{array} } \]
Five other orders for the iteration are possible; our choice depends on \(E\). As before, the braces and the brackets are usually omitted.
Finding a Triple Integral Using Cylindrical Coordinates
Give a geometric interpretation of the triple integral \begin{equation*} \int_{-1}^{1}\int_{-\sqrt{1-x^{2}}}^{\sqrt{1-x^{2}}}\int_{0}^{2\sqrt{ 1-x^{2}-y^{2}}}\,{\it dz}\,{\it dy}\,{\it dx} \end{equation*}
Then use cylindrical coordinates to find the triple integral.
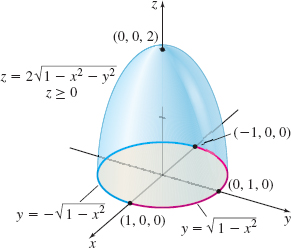
Solution The solid \(E\) of integration and its projection onto the \(xy\)-plane can be described by the inequalities \begin{equation*} 0\leq z\leq 2\sqrt{1-x^{2}-y^{2}}\qquad -\sqrt{1-x^{2}}\leq y\leq \sqrt{1-x^{2}} \qquad -1\leq x\leq 1 \end{equation*}
The limits of integration on \(z\) are \(z=0\) and \(z=2\sqrt{1-x^{2}-y^{2}}= \sqrt{4-4x^{2}-4y^{2}}\) or, equivalently, \(z^{2}=4-4x^{2}-4y^{2},\) \(z\geq 0.\) We can interpret the integral as the volume of a solid \(E\) that is the upper half of the ellipsoid \(4x^{2}+4y^{2}+z^{2}=4,\) \(z\geq 0,\) as shown in Figure 55. From the \(x\) and \(y\) limits of integration, the projection onto the \(xy\)-plane is the region \(R\) enclosed by the circle \(x^{2}+y^{2}=1\).
To find the integral, we convert the rectangular coordinates to cylindrical coordinates. Then \[ z=2\sqrt{1-x^{2}-y^{2}}=2\sqrt{1-(x^{2}+y^{2}) }=2\sqrt{1-r^{2}} \]
The projection onto the \(xy\)-plane is the region enclosed by the circle \(x^{2}+y^{2}=1.\) So in cylindrical coordinates, we have \[ 0\leq z\leq 2\sqrt{1-r^{2}} \qquad 0\leq r\leq 1\qquad 0\leq \theta \leq 2\pi \]
Then \[ \begin{array}{lll} \int_{-1}^{1}\int_{-\sqrt{1-x^{2}}}^{\sqrt{1-x^{2}}}\int_{0}^{2\sqrt{ 1-x^{2}-y^{2}}}\,{\it dz}\,{\it dy}\,{\it dx}& =&\int_{0}^{2\pi }\int_{0}^{1}\int_{0}^{2\sqrt{ 1-r^{2}}}\,{\it dz}\,r\,dr\,d\theta\\ &=&\int_{0}^{2\pi }\int_{0}^{1} \big[ z\big] _{0}^{2\sqrt{1-r^{2}}}r\,dr\,d\theta =\int_{0}^{2\pi }\int_{0}^{1}2r\sqrt{1-r^{2}}\ dr\,d\theta \\[5pt] & =&\int_{0}^{2\pi }\left[ -\dfrac{2}{3}(1-r^{2})^{3/2}\right] _{0}^{1}\,d\theta =\dfrac{2}{3}\int_{0}^{2\pi }d\theta =\dfrac{4\pi }{3} \end{array} \]
953
The value of the triple integral \(\dfrac{4\pi }{3}\) equals the volume \(V\) of the solid. That is, \[ V=\dfrac{4\pi }{3} \hbox{ cubic units} \]
NOW WORK
Problem 19.
Finding the Volume of a Solid Using Cylindrical Coordinates
Find the volume of the solid enclosed by the hemisphere \( x^{2}+y^{2}+z^{2}=4,\) \(z\geq 0,\) and the cylinder \((x-1)^{2}+y^{2}=1\).
Solution Figure 56(a) shows the hemisphere and the part of the cylinder whose volume we seek.
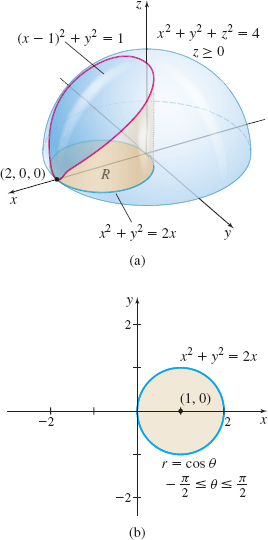
Because \(x^{2}+y^{2}\) appears in the equation of both the hemisphere and cylinder, we use cylindrical coordinates. The equation of the hemisphere is \[ \begin{array}{@{\hspace*{-1pc}}l@{\quad}rlrl} \hbox{Rectangular Coordinates:} &x^{2}+y^{2}+z^{2}&=4, z\geq 0\\ \hbox{Cylindrical Coordinates:} &r^{2}+z^{2}&=4, z\geq 0, \hbox{ or equivalently, } z=\sqrt{4-r^{2}} \end{array} \]
The equation of the region in the \(xy\)-plane above which the surface lies is given by: \[ \begin{eqnarray*} \hbox{Rectangular Coordinates:} & (x-1)^{2}+y^{2}&=1 & \\ & x^{2}+y^{2}&=2x & & \\ \hbox{Cylindrical Coordinates:} & r^{2}&=2( r\cos \theta ) & &{\color{#0066A7}{\hbox{$-\dfrac{\pi }{2} \leq \theta \leq \dfrac{\pi }{2}$}}} \\ & r&=2\cos \theta \end{eqnarray*} \]
See Figure 56(b).
The solid \(E\) whose volume we seek is given by \(0\leq z\leq \sqrt{4-r^{2}},\) \( 0\leq r\leq 2\cos \theta \), and \(-\dfrac{\pi }{2}\leq \theta \leq \dfrac{\pi }{2}.\) The volume \(V\) of the solid is \[ \begin{eqnarray*} V& =&\iiint\limits_{\kern-3ptE}{\it dV}=\iiint\limits_{\kern-3ptE}r\,dr\,d\theta \,{\it dz} \underset{\underset{{\color{#0066A7}{\hbox{Use symmetry}}}}{\color{#0066A7}{\uparrow}}}{=} 2\int_{0}^{\pi /2}\int_{0}^{2\cos \theta }\int_{0}^{\sqrt{4-r^{2}} }r\,{\it dz}\,dr\,d\theta \notag \\[-17pt] && \\[4pt] & =& 2 \int_{0}^{\pi /2}\int_{0}^{2\cos \theta }r\big[ z\big] _{0}^{\sqrt{4-r^{2}}}\,dr\,d\theta =2\int_{0}^{\pi /2}\int_{0}^{2\cos \theta }r( 4-r^{2}) ^{1/2}\,dr\,d\theta \\[4pt] &=&- \int_{0}^{\pi /2}\left[ \dfrac{2}{3}(4-r^{2})^{3/2}\right] _{0}^{2\cos \theta}\,d\theta \notag \\[4pt] &=&\dfrac{2}{3}\int_{0}^{\pi /2}[8-(4-4\cos ^{2}\theta )^{3/2}]\,d\theta =\dfrac{16}{3}\int_{0}^{\pi /2}(1-\sin ^{3}\theta )\,d\theta \\[4pt] &=&\dfrac{8\pi}{3} -\dfrac{32}{9} \hbox{cubic units } \end{eqnarray*} \]
NOW WORK
Problems 27 and 33.
Finding the Moment of Inertia of a Solid
Find the moment of inertia about the \(z\)-axis of a homogeneous solid \(E\) of mass density \(\rho \) enclosed by the paraboloid \(z=1-x^{2}-y^{2}\) and the \(xy\) -plane.
Solution In cylindrical coordinates, the solid \(E\) is enclosed on the top by the paraboloid \(z=1-x^{2}-y^{2}=1-r^{2}\) and on the bottom by \( z=0.\) In the \(xy\)-plane, the region is bounded by the circle \(x^{2}+y^{2}=1.\) So, we have \[ 0\leq \theta \leq 2\pi\qquad 0\leq r\leq 1\qquad \qquad 0\leq z\leq 1-r^{2} \]
954
The moment of inertia \(I_{z}\) about the \(z\)-axis is \[ \begin{eqnarray*} I_{z}& =&\iiint\limits_{\kern-3ptE}r^{2}\rho \,dV=\rho \iiint\limits_{\kern-3ptE}r^{2}r\,dr\,d\theta \,dz=\rho \int_{0}^{2\pi }\!\int_{0}^{1}\int_{0}^{1-r^{2}}r^{3}\,dz\,dr\,d\theta\\ & =&\rho \int_{0}^{2\pi }\int_{0}^{1}r^{3}(1-r^{2})\,dr\,d\theta =\rho \int_{0}^{2\pi }\left[ \dfrac{r^{4}}{4}-\dfrac{r^{6}}{6}\right] _{0}^{1}\,d\theta =\rho \int_{0}^{2\pi }\dfrac{1}{12}\,d\theta =\dfrac{\pi }{6} \rho \qquad \end{eqnarray*} \]
NOW WORK
Problem 43.
Finding the Moment of Inertia of a Sphere
![]() Find the moment of inertia of a homogeneous solid \(E\) in the shape of a sphere of radius 2 about a diameter.
Find the moment of inertia of a homogeneous solid \(E\) in the shape of a sphere of radius 2 about a diameter.
- Set up the integral to find the moment of inertia of the sphere about a diameter.
- Use a CAS to find the moment of inertia from (a).
Solution (a) Let \(\rho \) denote the constant mass density of the sphere of radius \(2.\) We position the sphere so that its center is at the origin. The equation of the sphere is then \(x^{2}+y^{2}+z^{2}=4\), or, in cylindrical coordinates, \(r^{2}+z^{2}=4\). If we use the \(z\)-axis as the diameter, the moment of inertia about a diameter is given by the moment of inertia \(I_{z}\) about the \(z\)-axis. Then \[ I_{z}=\iiint\limits_{\kern-3ptE}r^{2}\rho \,dV=\rho \int_{0}^{2\pi }\int_{0}^{2}\int_{-\sqrt{4-r^{2}}}^{\sqrt{4-r^{2}}}r^{3}\,dz\,dr\,d\theta \]
(b) We use a CAS to find \[ I_{z}=\rho \int_{0}^{2\pi }\int_{0}^{2}\int_{-\sqrt{4-r^{2}}}^{\sqrt{4-r^{2}} }r^{3}\,dz\,dr\,d\theta =\dfrac{256\pi \rho }{15} \]