14.8 Assess Your Understanding
Concepts and Vocabulary
Question
In spherical coordinates, the number \(\rho\) equals the distance from the _____ to the point \(P.\)
Question
In spherical coordinates, \(\phi\) is the angle between the positive _____ and the line segment \({\it OP}.\)
Question
True or False To change spherical coordinates \( ( \rho ,\theta ,\phi)\) to rectangular coordinates, use the equations \(x=\rho \sin \phi \cos \phi,\) \(y=\rho \sin \phi \sin \theta,\) and \(z=\rho \cos \theta.\)
Question
True or False In spherical coordinates \(\left( \rho ,\theta ,\phi \right),\) \(\rho = \sqrt{x^{2}+y^{2}+z^{2}},\) where \((x, y, z)\) are the rectangular coordinates of the point \(P.\)
Question
What is the differential \({\it dV}\) of the volume \(V\) in spherical coordinates?
Question
In spherical coordinates, the surface described by the equation \(\rho =a,\) where \(a \gt 0\) is a constant, is a(n) _____.
961
Skill Building
In Problems 7 and 8, fill in the missing coordinates. The three ordered triples represent the rectangular \((x, y, z)\), cylindrical \((r, \theta ,z)\), and spherical coordinates \((\rho ,\theta ,\phi),\) respectively, of some point in space.
Question
| \((x, y, z)\) | \((r, \theta ,z)\) | \((\rho, \theta, \phi)\) |
| \((1,\,\_\kern-.5pt\_,\,\_\kern-.5pt\_)\) | \(\left( \_\kern-.5pt\_,\,\_\kern-.5pt\_,\dfrac{-2\sqrt{3}}{3}\right)\) | \(\left(\_\kern-.5pt\_,\dfrac{\pi}{6},\,\_\kern-.5pt\_\right)\) |
Question
| \((x, y, z)\) | \((r, \theta, z)\) | \((\rho, \theta, \phi)\) |
| \((\_\kern-.5pt\_,\,\_\kern-.5pt\_,2\sqrt{2})\) | \((\sqrt{8},\,\_\kern-.5pt\_,\,\_\kern-.5pt\_)\) | \(\left( \_\kern-.5pt\_,\,\dfrac{\pi}{6},\,\_\kern-.5pt\_\right)\) |
In Problems 9–16, convert each point given in rectangular coordinates to spherical coordinates.
Question
\((-\sqrt{2},- \sqrt{2},2 \sqrt{3})\)
Question
\((-1,\sqrt{3},2)\)
Question
\((1,1,\sqrt{2})\)
Question
\(( 1,-\sqrt{3},-2 )\)
Question
\((1, 2, 3)\)
Question
\((1, -1, \sqrt{2})\)
Question
\((0, 3\sqrt{3}, 3)\)
Question
\((-5\sqrt{3}, 5, 0)\)
In Problems 17–20, find each iterated integral.
Question
\(\int_{0}^{\pi /2}\int_{0}^{\sin \phi }\int_{0}^{\pi /4}\rho ^{2}\sin \phi \,d\theta \,d\rho \,d\phi\)
Question
\(\int_{0}^{\pi /2}\int_{0}^{\pi /2}\int_{0}^{\sin \phi }\rho ^{2}\sin \phi \cos \phi \,d\rho \,d\theta \,d\phi\)
Question
\(\int_{0}^{2\pi}\int_{0}^{\pi /4}\int_{0}^{\sec \phi }\rho ^{2}\sin ^{2}\phi \,d\rho \,d\phi \,d\theta\)
Question
\(\int_{0}^{\pi /4}\int_{0}^{\cos \phi }\int_{0}^{2\pi }\rho ^{2}\sin \phi \,d\theta \,d\rho \,d\phi\)
In Problems 21–24, use spherical coordinates to find each triple integral.
Question
\(\int_{-2}^{2}\int_{-\sqrt{4-y^{2}}}^{\sqrt{4-y^{2}} }\int_{2}^{2+\sqrt{4-x^{2}-y^{2}}}y\,{\it dz}\,{\it dx}\,{\it dy}\)
Question
\(\int_{-3}^{3}\int_{-\sqrt{9-x^{2}}}^{\sqrt{9-x^{2}}}\int_{- \sqrt{9-x^{2}-y^{2}}}^{\sqrt{9-x^{2}-y^{2}}}( x^{2}z+y^{2}z+z^{3}) \, {\it dz}\,{\it dy}\,{\it dx}\)
Question
\(\int_{0}^{1}\int_{0}^{\sqrt{1-y^{2}}}\int_{\sqrt{x^{2}+y^{2} }}^{\sqrt{1-x^{2}-y^{2}}}( x^{2}+y^{2}+z^{2}) ^{3/2}\,{\it dz}\,{\it dx}\,{\it dy}\)
Question
\(\int_{0}^{1}\int_{0}^{\sqrt{1-y^{2}}}\int_{0}^{\sqrt{ 1-x^{2}-y^{2}}}e^{( x^{2}+y^{2}+z^{2}) ^{3/2}}\,{\it dz}\,{\it dx}\,{\it dy}\)
Applications and Extensions
Question
Use spherical coordinates to integrate \(f(x,y,z)= \sqrt{x^{2}+y^{2}+z^{2}}\) over the solid above the cone \(z=-\sqrt{ 3x^{2}+3y^{2}}\) and inside the sphere \(x^{2}+y^{2}+z^{2}=4\).
Question
Use spherical coordinates to integrate \(f(x, y, z)=\sqrt{ x^{2}+y^{2}+z^{2}}\) over the solid between the spheres \(x^{2}+y^{2}+z^{2}=1\) and \(x^{2}+y^{2}+z^{2}=4.\)
In Problems 27 and 28, use either cylindrical or spherical coordinates to find each triple integral.
Question
\(\int_{0}^{2}\int_{0}^{2}\int_{0}^{\sqrt{4-x^{2}}}\sqrt{x^{2}+y^{2}} {\it dy}\,{\it dx}\,{\it dz}\)
Question
\(\int_{0}^{2}\int_{0}^{\sqrt{4-y^{2}}}\int_{0}^{\sqrt{4-x^{2}-y^{2}}} \dfrac{2z}{\sqrt{x^{2}+y^{2}}}\,{\it dz}\,{\it dx}\,{\it dy}\)
In Problems 29 and 30, set up the triple integral \( \iiint\limits_{E}f(x, y, z)\, {dV}\) for \(E\) in rectangular, cylindrical, and spherical coordinates.
Question
\(E\) is a sphere of radius \(a\) with its center at the origin.
Question
\(E\) is the solid inside the cylinder \(x^{2}+y^{2}=4\) and inside the sphere \(x^{2}+y^{2}+z^{2}=9\).
The integrals in Problems 31 and 32 are given in spherical coordinates. Express each integral using rectangular coordinates. Do not find the integral.
Question
\(\int_{0}^{\pi}\int_{3\pi /4}^{\pi}\int_{0}^{4}\rho ^{5}\cos \phi \sin\phi \,d\rho \,d\phi \,d\theta\)
Question
\(\int_{\pi /2}^{3\pi /2}\int_{\pi /2}^{\pi }\int_{0}^{2} \dfrac{\rho ^{4}\sin \phi \cos \phi }{\rho ^{2}+3}\,d\rho \,d\phi \,d\theta\)
Question
Volume Use spherical coordinates to find the volumes of the two solids obtained when the hemisphere, \(z=\sqrt{ 25-x^{2}-y^{2}}\), is sliced by the plane \(x=2\).
Question
Volume Find the volume of the solid enclosed on the outside by the sphere \(\rho =2\) and on the inside by the surface \(\rho =1+\cos \phi\).
Question
Volume Find the volume cut from the sphere \(\rho =a\) by the cone \(\phi =\alpha\).
Question
Mass Use spherical coordinates to find the mass of the solid in the first octant between the spheres \(x^{2}+y^{2}+z^{2}=a^{2}\) and \( x^{2}+y^{2}+z^{2}=b^{2}\), where \(a \gt b,\) if the mass density at any point is inversely proportional to its distance from the origin.
Question
Mass Find the mass of a ball of radius \(a\) if the mass density of the sphere is proportional to the square of the distance from its center.
Question
Mass A solid occupies the region \(\sqrt{x^{2}+y^{2}}\leq z\leq 1\) and has mass density \(\delta (x, y, z)=z\sqrt{x^{2}+y^{2}+z^{2}}\). Find its mass.
Question
Center of Mass Find the center of mass of a solid hemisphere of radius \(a\) if the mass density is proportional to the distance from the center.
Question
Center of Mass Find the center of mass of a solid hemisphere if the mass density is proportional to the distance from the axis of symmetry.
Question
Center of Mass Find the center of mass of a homogeneous solid enclosed from above by the sphere \(x^{2}+y^{2}+z^{2}=9\) and from below by the half-cone \(z=\sqrt{x^{2}+y^{2}}\).
Question
Center of Mass Find the center of mass of a homogeneous solid in the shape of the wedge bounded by \(x^{2}+y^{2}=16\), \(z=2y\), \(y\geq 0\), \( z\geq 0\).
Question
Moment of Inertia Find the moment of inertia of a homogeneous solid in the shape of a sphere of radius \(2\) about a diameter.
962
Question
Moment of Inertia Show that the moment of inertia of a homogeneous solid in the shape of a sphere of radius \(a\) about a diameter is \(I=\) \(\dfrac{8}{15}a^{5}\pi.\)
Question
Centroid Use spherical coordinates to find the centroid of a hemisphere of radius \(a\), whose base is on the \(xy\)-plane.
Question
Gravitational Force The magnitude of the resultant gravitational force \(F\) of a solid hemisphere \(E\) of radius \(a\) and constant mass density \(\delta\) on a unit mass particle situated at the center of the base of the hemisphere is given by the triple integral \[ F=k\delta \iiint\limits_{E}\dfrac{\cos \phi }{\rho ^{2}}\,{dV} \]
where the center of the sphere is at the origin. Find the force \(F\).
Question
Modeling an Asteroid—I On December 12, 2011, the Cassini mission spacecraft made its closest approach to the asteroid Dione. As with the planets, Dione is denser inside than at the surface because gravity compresses the matter. Suppose on Dione the density at the center is \(2.50 \text{g}/ \text{cm}^{3}=2500 \text{kg}/\text{m}^{3},\) the density at the surface is \(1.25 \text{g}/\text{cm}^{3}=1250 \text{kg}/\text{m}^{3},\) and the radius is \(560 \text{km}\). Model the density \(D\) as \(D=D_{0}e^{-k\rho}\), where \(\rho\) is the distance from the center and \(k\) is a constant to be determined.

- Using this model, find \(k\) and \(D_{0}\).
- Use this model to find the mass of Dione. Test the reasonableness of the model by comparing the calculated mass with the measured mass, which is \(1.095\times 10^{21} \text{kg}\).
Question
Modeling an Asteroid—II Refer to Problem 47. Instead of an exponential function, model the density of Dione as a linear decrease in density from \(2.50 \text{g}/ \text{cm}^{3}\) at the center of Dione to \(1.25 \text{g}/ \text{cm}^{3}\) at its surface. Find the mass of Dione using this model and compare it with the measured value (\(1.05\times 10^{21} \text{kg})\).
Challenge Problem
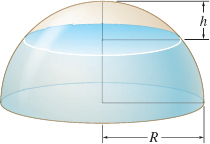
Question
Volume A spherical cap is a portion of height \(h\) of a sphere of radius \(R.\) See the figure. Using a triple integral and an appropriate coordinate system, show that the volume of the cap is \(V=\dfrac{1 }{3}\pi h^{2}( 3R-h).\)