OBJECTIVES

When you finish this section, you should be able to:

1. Find a Jacobian in two variables (p. 963)
2. Change the variables of a double integral using a Jacobian (p. 964)
3. Change the variables of a triple integral using a Jacobian (p. 965)

NOTE

In making a change in variables, the functions \(g_1\) and \(g_2\) are one-to-one.

spanDEFINITIONspan Jacobian: Two Variables

For a change of variables from \(x,\) \(y\) to \(u,\) \(v\) given by \[\bbox[5px, border:1px solid black, #F9F7ED]{ x=g_{1}(u,v)\qquad y=g_{2}(u,v) } \]

the Jacobian of \(x\) and \(y\) with respect to \(u\) and \(v\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{\partial (x,y)}{\partial (u,v)} =\left\vert \begin{array}{c@{\quad}c} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\[9pt] \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{array} \right\vert =\dfrac{\partial x}{\partial u}\dfrac{\partial y}{\partial v}- \dfrac{\partial x}{\partial v}\dfrac{\partial y}{\partial u} } \]

NEED TO REVIEW?

Determinants are discussed in Section 10.5, p. 725.

ORIGINS

Jacobians are named after the German mathematician Carl Gustav Jacobi (1804–1851). Jacobi was a child prodigy. By age 12, he had met the entrance requirements for university admission. He studied mathematics, Latin, and Greek and became a professor at the University of Köorionigsberg. Although he worked with functional determinants, he is most noted for his work with elliptic functions. Jacobi died of smallpox at age 46.

Finding a Jacobian

Show that in changing from rectangular coordinates \((x,y)\) to polar coordinates \((r,\theta )\), the Jacobian of \(x\) and \(y\) with respect to \(r\) and \(\theta \) is \(r\).

Solution To change the variables from rectangular to polar coordinates, we use the equations \begin{equation*} x=r\cos \theta \qquad y=r\sin \theta \end{equation*}

The partial derivatives are \[ \dfrac{\partial x}{\partial r}=\cos \theta \qquad \dfrac{\partial x}{ \partial \theta }=-r\sin \theta \qquad \dfrac{\partial y}{\partial r}=\sin \theta \qquad \dfrac{\partial y}{\partial \theta }=r\cos \theta \]

The Jacobian of \(x,y\) with respect to \(r,\theta \) is \begin{eqnarray*} \dfrac{\partial (x,y)}{\partial (r,\theta )}&=&\left\vert \begin{array}{c@{\quad}c} \dfrac{\partial x}{\partial r} & \dfrac{\partial x}{\partial \theta } \\[9pt] \dfrac{\partial y}{\partial r} & \dfrac{\partial y}{\partial \theta } \end{array} \right\vert =\left\vert \begin{array}{l@{\quad}r} \cos \theta & -r\sin \theta \\[3pt] \sin \theta & r\cos \theta \end{array} \right\vert =\cos \theta \cdot r\cos \theta -\sin \theta (-r\sin \theta)\\[4pt] &=&r\cos ^{2}\theta +r\sin ^{2}\theta =r \end{eqnarray*}

NOW WORK

Problem 9.

THEOREM Change in the Variables in a Double Integral

Suppose \(R\) is a closed, bounded region of the \(xy\)-plane and \(R^{\#}\) is a closed, bounded region of the \(uv\)-plane, where each point in \(R\) corresponds to one and only one point in \(R^{\#}\) when the change of variables \(x=g_{1}(u,v)\), \(y=g_{2}(u,v)\) is made. If:

• \(f\) is continuous on \(R,\)
• \(g_{1}\) and \(g_{2}\) have continuous partial derivatives on \(R^{\#}\), and
• the Jacobian \(\dfrac{\partial (x,y)}{\partial (u,v)}\neq 0\) on \(R^{\#}\),

then \[\bbox[5px, border:1px solid black, #F9F7ED]{ \displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,d\!A=\displaystyle\iint\limits_{\kern-3ptR^{ \#}}f(g_{1}(u,v),g_{2}(u,v))\left\vert \dfrac{\partial (x,y)}{\partial (u,v)} \right\vert \,du\,dv } \]

Using a Jacobian in a Double Integral

Find \(\iint\limits_{\kern-3ptR}y\,d\!A\), where \(R\) is the region enclosed by the lines \(2x+y=0\), \(\ \ 2x+y=3\), \(x-y=0\), and \(x-y=2\).

Solution We use the change of variables \(u=2x+y\) and \(v=x-y\). Then the lines \(2x+y=0\) and \(2x+y=3\) in the \(xy\)-plane correspond to the lines \(u=0\) and \(u=3\) in the \(uv\)-plane. The lines \(x-y=0\) and \(x-y=2\) in the \(xy\)-plane correspond to the lines \(v=0\) and \(v=2\) in the \(uv\)-plane. As Figure 63 shows, the region \(R\) in the \(xy\)-plane is a parallelogram and the region \(R^{\#}\) in the \(uv\)-plane is a rectangle.

Figure 63

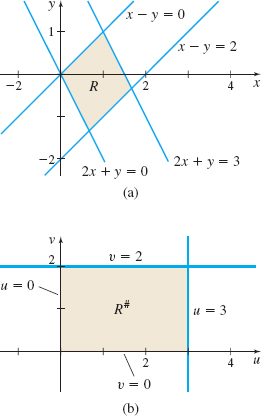
To find the Jacobian, we need to express \(x\) and \(y\) as functions of \(u\) and \(v\). We can achieve this by solving the system of equations \(\left\{ \begin{array}{l} u=2x+y \\ v=x-y \end{array} \right. \) for \(x\) and \(y.\) Then \[ x=\dfrac{u+v}{3} \qquad y=\dfrac{u-2v}{3} \]

The Jacobian is \begin{equation*} \dfrac{\partial (x,y)}{\partial (u,v)}=\left\vert \begin{array}{c@{\quad}c} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v}\\[3pt] \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{array} \right\vert =\left\vert \begin{array}{l@{\quad}r} \dfrac{1}{3} & \dfrac{1}{3}\\[3pt] \dfrac{1}{3} & -\dfrac{2}{3} \end{array} \right\vert =-\dfrac{2}{9}-\dfrac{1}{9}=-\dfrac{1}{3} \end{equation*}

Using this change of variables, the integral \(\iint\limits_{\kern-2ptR}y\,d\!A\) becomes \[ \begin{eqnarray*} \iint\limits_{\kern-3ptR}y\,d\!A &=&\displaystyle\iint\limits_{\kern-3ptR^{\#}}\dfrac{u-2v}{3}\cdot \left\vert -\dfrac{1}{3}\right\vert \,du\,dv=\int_{0}^{2}\int_{0}^{3}\dfrac{1}{9}(u-2v)\,du\,dv=\dfrac{1}{9}\int_{0}^{2}\left[ \dfrac{u^{2}}{2}-2uv\right]_{0}^{3}\,dv\\ &=&\dfrac{1}{9}\int_{0}^{2}\left( \dfrac{9}{2}-6v\right) {dv}=\dfrac{1}{9}\left[\dfrac{9v}{2}-3v^{2}\right] _{0}^{2}=\dfrac{1}{9}(9-12)=-\dfrac{1}{3} \end{eqnarray*} \]

NOW WORK

Problem 21.

Using a Jacobian in a Double Integral

Find \begin{equation*} \displaystyle\iint\limits_{\kern-3ptR}(x+y)\sin (x-y)\,d\!A \end{equation*}

where \(R\) is the region enclosed by \(y=x\), \(\ y=x-2\), \(\ y=-x\), and \(\ y=-x+1 \).

Figure 64

Solution The integrand \((x+y)\sin (x-y)\) suggests changing the variables to \(u=x+y\) and \(v=x-y\). Then the lines \(x-y=0\), \(\ x-y=2\), \(\ x+y=0\), and \(\ x+y=1\) in the \(xy\)-plane define the region \(R\), and the lines \(v=0,\) \(v=2,\) \(u=0,\) and \(u=1\) in the \(uv\)-plane define the region \(R^{\#}\). See Figure 64. We solve the system of equations \(\left\{ \begin{array}{l} u=x+y \\[3pt] v=x-y \end{array} \right. \) for \(x\) and \(y\), and obtain \begin{equation*} x=\dfrac{u+v}{2}\qquad y=\dfrac{u-v}{2} \end{equation*}

Using these equations, the Jacobian is \begin{equation*} \dfrac{\partial (x,y)}{\partial (u,v)}=\left\vert \begin{array}{l@{\quad}r} \dfrac{1}{2} & \dfrac{1}{2} \\[9pt] \dfrac{1}{2} & -\dfrac{1}{2} \end{array} \right\vert =-\dfrac{1}{4}-\dfrac{1}{4}=-\dfrac{1}{2} \end{equation*}

The integral under this change of variables becomes \begin{eqnarray*} \iint\limits_{\kern-3ptR}(x+y)\sin (x-y)\,d\!A& =&\iint\limits_{\kern-3ptR^{\#}}u\sin v\cdot \left\vert -\dfrac{1}{2}\right\vert \,du\,dv=\dfrac{1}{2}\int_{0}^{1} \int_{0}^{2}u\sin v\,dv\,du \notag \\ & =&\dfrac{1}{2}\int_{0}^{1}\big[u(-\cos v)\big] _{0}^{2}\,du= \dfrac{1}{2}(1-\cos 2)\int_{0}^{1}u\,du \notag \\[4.5pt] & =&\dfrac{1}{4}(1-\cos 2) \end{eqnarray*}

NOW WORK

Problem 23.

spanDEFINITIONspan Jacobian: Three Variables

For a change of variables from \(x,\) \(y,\) \(z\) to \(u,\) \(v,\) \(w\) given by \[\bbox[5px, border:1px solid black, #F9F7ED]{ x=g_{1}(u,v,w)\qquad y=g_{2}(u,v,w)\qquad z=g_{3}(u,v,w) } \]

the Jacobian of \(x,\) \(y,\) and \(z\) with respect to \(u,\) \(v,\) and \(w\) is given by \[\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{\partial (x,y,z)}{ \partial (u,v,w)}=\left\vert \begin{array}{c@{\quad}c@{\quad}c} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} & \dfrac{ \partial x}{\partial w} \\[9pt] \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} & \dfrac{ \partial y}{\partial w} \\[9pt] \dfrac{\partial z}{\partial u} & \dfrac{\partial z}{\partial v} & \dfrac{ \partial z}{\partial w} \end{array} \right\vert } \]

NOW WORK

Problem 13.

THEOREM Change in the Variables in a Triple Integral

Suppose \(E\) is a closed, bounded solid of \(xyz\)-space and \(E^{\#}\) is a closed, bounded solid of \(uvw\)-space, where each point in \(E\) corresponds to one and only one point in \(E^{\#}\) when the change of variables \(x=g_{1}(u,v,w)\), \(\ y=g_{2}(u,v,w),\) and \(z=g_{3}(u,v,w)\) is made. If:

• \(f\) is continuous on \(E\),
• \(g_{1},\) \(g_{2},\) and \(g_{3}\) have continuous partial derivatives on \( E^{\#}\), and
• the Jacobian \(\dfrac{\partial (x,y,z)}{\partial (u,v,w)}\neq 0\) on \( E^{\#}\), then

\[\bbox[5px, border:1px solid black, #F9F7ED]{ \iiint\limits_{\kern-3ptE}f(x,y,z)\,{\it dV}=\iiint\limits_{\kern-3ptE^{ \#}}f(g_{1}(u,v,w),g_{2}(u,v,w),g_{3}(u,v,w))\left\vert \dfrac{\partial (x,y,z)}{\partial (u,v,w)}\right\vert \,du\,dv\,dw } \]

Using a Jacobian in a Triple Integral

Find \(\iiint\limits_{\kern-3ptE} y\,{\it dV},\) where \(E\) is the solid enclosed by the planes \(2x+y=0,\) \(2x+y=3,\) \(x-z=0,\) \(x-z=2\), \(z=0,\) and \(z=4.\)

Figure 65

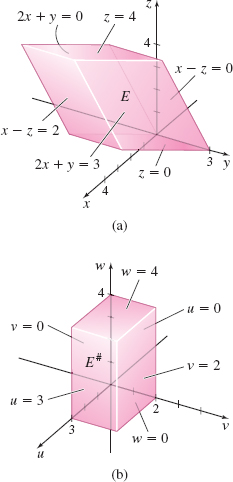
Solution The solid \(E\) is the slanted parallelepiped shown in Figure 65(a). The change of variables \(u=2x+y,\) \(v=x-z,\) and \(w=z\) transforms \(E\) into the rectangular parallelepiped \(E^{\#}\) shown in Figure 65(b). \(E^{\#}\) is the solid enclosed by the planes \(u=0,\) \(u=3,\) \(v=0\), \( v=2,\) and \(w=0,\) \(w=4.\)

We solve the system of equations \(\left\{ \begin{array}{l} u=2x+y \\ v=x-z \\ w=z \end{array} \right. \) for \(x,\) \(y,\) and \(z\) and obtain \[ x=v+w \qquad y=u-2x=u-2 ( v+w ) =u-2v-2w \qquad z=w \]

The Jacobian is \begin{equation*} \dfrac{\partial (x,y,z)}{\partial (u,v,w)}=\left\vert \begin{array}{c@{\quad}c@{\quad}c} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} & \dfrac{ \partial x}{\partial w} \\[9pt] \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} & \dfrac{ \partial y}{\partial w} \\[9pt] \dfrac{\partial z}{\partial u} & \dfrac{\partial z}{\partial v} & \dfrac{ \partial z}{\partial w} \end{array} \right\vert = \left|\begin{array}{c@{\quad}c@{\quad}c} 0 & \hphantom{-}1 & \hphantom{-}1\\ 1 & -2 & -2\\ 0 & \hphantom{-}0 & \hphantom{-}1 \end{array}\right| =-1 \end{equation*}

The integral \(\iiint\limits_{\kern-3ptE}\,y\,{\it dV}\) under this change of variables becomes \[ \begin{array}{rcl} \displaystyle\iiint\limits_{\kern-3ptE}~y\,{\it dV} &=&\displaystyle\iiint\limits_{\kern-3ptE^{\#}}(u-2v-2w) \left\vert \dfrac{\partial (x,y,z)}{\partial (u,v,w)}\right\vert du\, dv\, dw=\int_{0}^{4}\int_{0}^{2}\int_{0}^{3}( u-2v-2w) \,du\,dv\,dw \notag\\ &=&\displaystyle\int_{0}^{4}\int_{0}^{2}\left[ \dfrac{u^{2}}{2}-2vu-2wu\right] _{0}^{3}dv\,dw=\int_{0}^{4}\int_{0}^{2}\left( \dfrac{9}{2}-6v-6w\right) dv\, dw \notag\\ &=&\displaystyle\int_{0}^{4}\left[ \dfrac{9}{2}v-3v^{2}-6wv\right] _{0}^{2}\, dw= \int_{0}^{4}( 9-12-12w) \, dw=\int_{0}^{4}( -3-12w) \, dw \notag\\ &=&\big[ -3w-6w^{2}\big] _{0}^{4}=-12-96=-108 \end{array} \]

NOW WORK

Problem 25.