14.2 Assess Your Understanding
920
Concepts and Vocabulary
Question
A closed, bounded region \(R\) that has a boundary consisting of two smooth curves, \(y=g_{1}(x)\) and \(y=g_{2}(x),\) defined on \(a\leq x\leq b,\) where \(g_{1}(x)\leq g_{2}(x)\) on \([a,b] \) and possibly a portion of the vertical lines \(x=a\) and \(x=b,\) is called a(n) ________ region.
Question
True or False The double integral of a function that is continuous on a closed, bounded, \(y\)-simple region \(R\) can be expressed as an iterated integral.
Question
True or False The region \(R\) enclosed by the parabola \(y=x^{2}+1\) and the line \(y=3x+1\) is both \(x\)-simple and \(y\)-simple.
Question
Explain why \(\int_{0}^{1}\left[ \int_{0}^{x}f(x,y)\, {\it dy}\right]\! {\it dx}\neq \int_{0}^{1}\left[ \int_{0}^{y}f(x,y)\,{\it dx}\right]\! {\it dy}.\)
Skill Building
In Problems 5–8, express \(\displaystyle\iint\limits_{\kern-3ptR} xy^2\,{\it dA}\) as an iterated integral in two ways:
- one with the integration with respect to \(x\) first;
- the other with the integration with respect to \(y\) first,
- find each double integral over the region \(R\).
Question
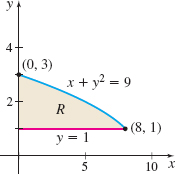
Question
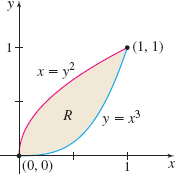
Question
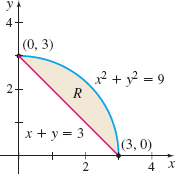
Question
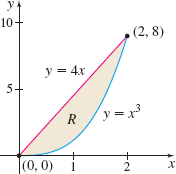
In Problems 9–24, find each iterated integral. Identify and graph the region \(R\) associated with each integral.
Question
\(\displaystyle\int_{0}^{1}\left[ \int_{x^{2}}^{\sqrt{x}}\,{\it dy}\right]\! {\it dx}\)
Question
\(\displaystyle\int_{0}^{1}\left[ \int_{y^{2}}^{\sqrt{y}}x\,{\it dx}\right]\! {\it dy}\)
Question
\(\displaystyle\int_{-1}^{2}\left[\int_{y^{2}}^{y+2}\,{\it dx}\right]\! {\it dy}\)
Question
\(\displaystyle\int_{0}^{1}\left[ \int_{x}^{2x}y\,{\it dy}\right]\! {\it dx}\)
Question
\(\displaystyle\int_{0}^{1}\left[ \int_{x}^{3x}xy\,{\it dy}\right]\! {\it dx}\)
Question
\(\displaystyle\int_{0}^{1}\left[ \int_{y}^{\sqrt{y}}x^{2}y\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{0}^{1}\left[ \int_{1}^{e^{y}}\dfrac{y}{x}\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{0}^{1}\left[\int_{0}^{x^{2}}xe^{y}\,{\it dy}\right]\! {\it dx}\)
Question
\(\int_{0}^{2}\left[ \int_{y}^{2y}xy\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{2}^{4}\left[ \int_{1}^{y^{2}}\dfrac{y}{x^{2}}\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{0}^{1}\left[ \int_{x^{2}}^{x}\sqrt{xy}\,{\it dy}\right]\! {\it dx}\)
Question
\(\int_{0}^{1}\left[\int_{x^{2}}^{x}\sqrt{x}\,{\it dy}\right]\! {\it dx}\)
Question
\(\int_{0}^{1}\left[ \int_{x}^{1}\dfrac{1}{x^{2}+1}\,{\it dy}\right]\! {\it dx}\)
Question
\(\int_{0}^{1}\left[ \int_{y}^{\sqrt{y}}(x^{2}+y^{2})\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{1}^{2}\left[ \int_{0}^{\ln x}xe^{y}\,{\it dy}\right]\! {\it dx}\)
Question
\(\int_{2}^{3}\left[ \int_{0}^{1/y}\ln y\,{\it dx}\right]\! {\it dy}\)
In Problems 25–28, find each double integral. Start by graphing the region \(R\). Pay particular attention to the boundary, since it determines the correct limits of integration.
Question
\(\displaystyle\iint\limits_{\kern-3ptR}(x+y)\,{\it dA},\) where \(R\) is the region enclosed by \(y=x^{2}\) and \(y^{2}=8x\)
Question
\(\displaystyle\iint\limits_{\kern-3ptR}(x^{2}-y^{2})\,{\it dA},\) where \(R\) is the region enclosed by \(y=x\) and \(y=x^{2}\)
Question
\(\displaystyle\iint\limits_{\kern-3ptR}y^{2}\,{\it dA},\) where \(R\) is the region enclosed by \(y=2-x\) and \(y=x^{2}\)
Question
\(\displaystyle\iint\limits_{\kern-3ptR}xy\,{\it dA},\) where \(R\) is the region enclosed by \(y^{2}=x+1\) and \(y=1-x\)
In Problems 29–36, use double integration to find the area of each region.
Question
Enclosed by the graphs of \(y=x^{3}\) and \(y=x^{2}\)
Question
Enclosed by the graphs of \(y=2 \sqrt{x}\) and \(y=\dfrac{x^{2}}{4}\)
Question
Enclosed by the graphs of \(y=x^{2}-9\) and \(y=9-x^{2}\)
Question
Enclosed by the graphs of \(x^{2}+y^{2}=16\) and \(y^{2}=6x\)
Question
Enclosed by the graph \(y=\dfrac{1}{\sqrt{x-1}}\), the \(x\) -axis, and the lines \(x=2\) and \(x=5\)
Question
Enclosed by the graphs of \(y=x^{3/2}\) and \(y=x\)
Question
Enclosed by the line \(x+y=3\) and the hyperbola \(xy=2\)
Question
Enclosed by the hyperbola \(xy=\sqrt{3}\) and the circle \(x^{2}+y^{2}=4\), in the first quadrant only
In Problems 37–44, change the order of integration of each iterated integral to obtain an equivalent expression.
Question
\(\int_{0}^{1}\left[ \int_{0}^{x}f(x,y)\,{\it dy}\right]\! {\it dx}\)
Question
\(\int_{0}^{2}\left[ \int_{y^{2}}^{2y}f(x,y)\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{0}^{a}\left[ \int_{0}^{\sqrt{a^{2}-y^{2}}}f(x,y)\,{\it dx}\right]\! {\it dy}\)
921
Question
\(\int_{0}^{2\sqrt[3]{2}}\left[ \int_{x^{2}/4}^{\sqrt{x}}f(x,y)\,{\it dy}\right]\! {\it dx}\)
Question
\(\int_{0}^{16}\left[\int^{y^{1/4}}_{y/8} f(x,y)\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{2}^{5}\left[ \int_{x^{2}-6x+9}^{x-1}f(x,y)\,{\it dy}\right]\! {\it dx}\)
Question
\(\int_{1}^{2}\left[ \int_{0}^{\ln y}f(x,y)\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{1}^{e}\left[ \int_{\ln x}^{1}f(x,y)\,{\it dy} \right]\! {\it dx}\)
In Problems 45–48, the functions \(f\) and \(g\) are continuous on a closed, bounded region \(R,\) \(\displaystyle\iint\limits_{\kern-3ptR}f(x,y)\, {\it dA}=8\) and \(\displaystyle\iint\limits_{\kern-3ptR}g(x,y)\, {\it dA}=-6\). Use properties of double integrals to find each double integral.
Question
\(\displaystyle\iint\limits_{\kern-3ptR}[ f(x,y) -g(x,y) ] \, {\it dA}\)
Question
\(\displaystyle\iint\limits_{\kern-3ptR}4f(x,y) \, {\it dA}\)
Question
\(\displaystyle\iint\limits_{\kern-3ptR}[ 3f(x,y) +4g(x,y) ] \, {\it dA}\)
Question
\(\displaystyle\iint\limits_{\kern-3ptR} [ 2f(x,y) +5g(x,y) ] \, {\it dA}\)
Applications and Extensions
Question
Area Find the area of the region \(R\) in the first quadrant enclosed by the graphs of \(y=6x-x^{2}\) and \(y=4x-8\) by partitioning \(R\) with a horizontal line through the point \((4,8)\). Refer to Figure 20.
Question
Area Use double integration to find the area in the first quadrant enclosed by the parabola \(x^{2}=9y\), the \(y\)-axis, and the circle \(x^{2}+y^{2}=10.\)
Volume In Problems 51–60, find the volume of each solid.
Question
The tetrahedron enclosed by the plane \(x+2y+z=2\) and the coordinate planes
Question
Enclosed by the elliptic paraboloid \(4x^{2}+9y^{2}=36\) and the planes \(z=0\) and \(z=1\)
Question
Below the paraboloid \(z=x^{2}+y^{2}\) and above the triangular region \(R \) formed by the \(x\)- and \(y\)-axes and the line \(x+y=1,\) as shown in the figure below.
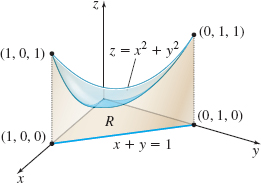
Question
Enclosed by the cylinder \(z=9-y^{2}\) and the planes \(x=0\), \(x=4\), and \(z=0\)
Question
Enclosed by the surface \(z=4-x^{2}-y^{2}\) and \(z=0\)
Question
Enclosed by the surfaces \(x^{2}+y^{2}=1\), \(z=x\), and \(z=x^{2}\)
Question
The solid bounded from above by the graph of \(z=x^{2}+y^{2}\), from below by the \(xy\)-plane, and on the sides by the cylinder \(x^{2}+y^{2}=1\), as shown in the figure.
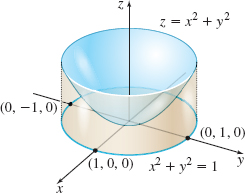
Question
Enclosed by a portion of the parabolic cylinder \(z=\dfrac{x^{2} }{2}\) and the four planes \(y=0\), \(y=x\), \(x=2\), and \(z=0\)
Question
Enclosed by the coordinate planes, the plane \(y=3\), and the surface \(z=y+1-x^{2}\)
Question
Enclosed by the surfaces \(z=xe^{y}\), \(z=0\), \(y=0\), \(x=1\), and \(y=x^{2}\)
In Problems 61–68. (a) graph the region associated with each iterated integral, (b) reverse the order of integration, and (c) find the new iterated integral.
Question
\(\int_{0}^{\sqrt{\pi /2}}\left[ \int_{y}^{\sqrt{\pi /2}}\sin x^{2}\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{0}^{1/2}\left[ \int_{2x}^{1}e^{y^{2}} {\it dy}\right]\! {\it dx}\)
Question
\(\int_{0}^{1}\left[ \int_{0}^{\sqrt{1-x^{2}}}\dfrac{1}{\sqrt{1-y^{2}}}\,{\it dy}\right]\! {\it dx}\)
Question
\(\int_{0}^{1}\left[ \int_{y}^{1}\dfrac{\sin x}{x}\,{\it dx}\right]{\it dy}\)
Question
\(\int_{0}^{1}\left[ \int_{y}^{1}\sqrt{2+x^{2}}\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{0}^{1}\left[ \int_{\sqrt[3]{x}}^{1}\sqrt{1+y^{4}}~{\it dy}\right]\! {\it dx}\)
Question
\(\int_{0}^{1}\left[ \int_{\sqrt{y}}^{1}e^{y/x}\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{0}^{1}\left[ \int_{\sin ^{-1}y}^{\pi /2}e^{\cos x}\,{\it dx}\right]\! {\it dy}\)
Question
Properties of Double Integrals Let \(R\) be the region enclosed by \(y=1\), \(y=-1\), \(x=0\), and \(x=1\); let \(R_{1}\) and \(R_{2}\) be the subregions of \(R\) in the first and fourth quadrants, respectively. Suppose \(f\) is continuous on \(R\) and \begin{eqnarray*} &&\displaystyle\iint\limits_{\kern-3ptR}3f(x,y)\,{\it dA}-2\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=\displaystyle\iint \limits_{\kern-3ptR_{2}}f(x,y)\,{\it dA}, \\[3pt] &&\displaystyle\iint\limits_{\kern-3ptR_{2}}5f(x,y)\,{\it dA}-2\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=18 \end{eqnarray*}
Find \(\displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}\).
Question
Properties of Double Integrals Let \(R\) be the region enclosed by \(y=0\), \(y=2\), \(x=-2\), and \(x=1\); let \(R_{1}\) and \(R_{2}\) be the subregions of \(R\) in the first and second quadrants, respectively. Suppose \(f\) is continuous on \(R\) and \begin{eqnarray*} &&\displaystyle\iint\limits_{\kern-3ptR_{2}}3f(x,y)\,{\it dA}-\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=2\displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA},\\[4pt] &&\displaystyle\iint\limits_{\kern-3ptR_{1}}4f(x,y)\,{\it dA}+\displaystyle\iint\limits_{\kern-3ptR_{2}}2f(x,y)\,{\it dA}=7 \end{eqnarray*}
Find \(\displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}\).
922
Question
Properties of Double Integrals Let \(R\) be the region enclosed by \(y=x\), \(y=-1\), and \(x=2\); let \(R_{1}\) and \(R_{2}\) be the subregions of \(R\) above the \(x\)-axis and below the \(x\)-axis, respectively. Suppose \(f\) is continuous on \(R\) and \begin{eqnarray*} &&2\displaystyle\iint\limits_{\kern-3ptR_2}f(x,y)\,{\it dA}-7\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=17\\[4pt] &&\displaystyle\iint\limits_{\kern-3ptR_{2}}f(x,y)\,{\it dA}-2\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=7 \end{eqnarray*}
Find \(\displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}\).
Question
Properties of Double Integrals Let \(R\) be the region enclosed by \(y=x^{2}+1\), \(y=0\), \(x=-1\), and \(x=2\); let \(R_{1}\) and \(R_{2}\) be the subregions of \(R\) in the first and second quadrants, respectively. Suppose \(f\) is continuous on \(R\) and \begin{eqnarray*} &&\displaystyle\iint\limits_{\kern-3ptR_2}6f(x,y)\,{\it dA}-3\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=-12\\[4pt] &&\displaystyle\iint\limits_{\kern-3ptR_{2}}4f(x,y)\,{\it dA}+2= \displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA} \end{eqnarray*}
Find \(\displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}\).
In Problems 73–76, each of the iterated integrals represents the volume of a solid. Describe the solid.
Question
\(\int_{0}^{1}\left[ \int_{0}^{\sqrt{1-x^{2}}}\sqrt{1-x^{2}-y^2}\,{\it dy}\right]\! {\it dx}\)
Question
\(\int_{0}^{2}\left[ \int_{0}^{\sqrt{4-y^{2}}}(4-x^2-y^2)\,{\it dx}\right]\! {\it dy}\)
Question
\(\int_{0}^{4}\left[ \int_{0}^{1}3\,{\it dy}\right]\! {\it dx}\)
Question
\(\int_{0}^{1}\left[ \int_{0}^{2}2\,{\it dy}\right]\! {\it dx}\)
Question
Find:
- \(\displaystyle\iint\limits_{\kern-3ptR}x\,{\it dA},\) where \(R\) is the region enclosed by the circle of radius 1 centered at the origin.
- \(4\displaystyle\iint\limits_{\kern-3ptR_{1}}x\,{\it dA},\) where \(R_{1}\) is the region in the first quadrant enclosed by the circle of radius 1 centered at the origin (This shows that although the region over which we are integrating is symmetric about the \(x\)-axis and the \(y\)-axis, we must also consider properties of the integrand on this region before we use symmetry.)
Question
- Find \[ \int_{1}^{e}\left[ \int_{0}^{\ln x}\dfrac{{\it dy}}{x}\right]\! {\it dx}. \]
- Reverse the order of integration and find the resulting iterated integral.
Question
- Find \[ \int_{0}^{\pi /2}\left[ \int_{0}^{\cos x}\sin x\,{\it dy}\right]\! {\it dx}. \]
- Reverse the order of integration and find the resulting iterated integral.
Question
Volume of a Liquid A tank in the shape of a half-cylinder is lying on its flat side. The radius of the tank is 1 m and its length is 4 m. If the tank is filled with liquid to a depth of \(a\) meters, what is the volume of the liquid? (Hint: Position the half cylinder as shown in the figure below.)
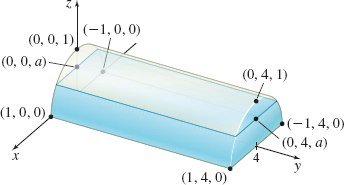
Question
Volume of a Liquid Repeat Problem 80 if the tank is buried so its rounded base is 1 m under the ground and its flat side is at ground level. See the figure below.
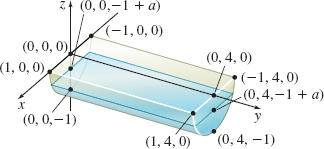
Question
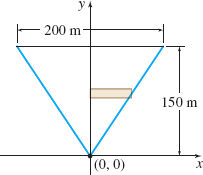
Damming a Valley A dam is built in a V-shaped valley. The top of the dam is \(200\) m wide and the lowest point in the V is \(150\) m below the top, as shown in the figure. The pressure \(P\) due to the water at a depth \(d\) meters below the surface is \(P=\rho gd\), where \(\rho =1000 \text{kg}/ \text{m}^{3}\) and \(g=9.8 \text{m}/ {\text s}^{2}\). What is the total outward force \(F\) from the water that this dam must be able to withstand? Express your answer in both newtons and pounds using the fact that \(1 {\text N} \approx 0.2248 \text{lb}\). (Recall that pressure is \(P=\dfrac{F}{A},\) so the force \(F=PA.)\)
Question
Explain if the following equality is true or false without finding the exact value of the two integrals: \[ \int_{-3}^{3}\int_{-\sqrt{ 9-y^{2}}}^{\sqrt{9-y^{2}}} ( 7-x)\,{\it dx}\, {\it dy}=4\int_{0}^{3}\int_{0}^{ \sqrt{9-y^{2}}}( 7-x)\,{\it dx}\, {\it dy} \]
Question
Volume Find the volume of the tetrahedron enclosed by the coordinate planes and the plane \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\). (Assume that \(a,b\), and \(c\) are positive.)
Question
Find \(\displaystyle\iint\limits_{\kern-3ptR}xy\,{\it dA}\), where \(R\) is the region enclosed by \(y=4-x^{2}\) and \(y=x^{2}\) to the right of the \(y\)-axis.
Question
Find \(\displaystyle\iint\limits_{\kern-3ptR}xy\,{\it dA}\), where \(R\) is the region enclosed by \(x=4-y^{2}\) and \(x=y^{2}\) above the \(x\)-axis.
Question
Find \(\displaystyle\iint\limits_{\kern-3ptR}e^{\sqrt{x}}\,{\it dA}\), where \(R\) is the dregion enclosed by \(y=x\), \(x=1\), \(y=0\).
923
Question
- Graph the region \(R\) defined by \(0\leq a\leq y\leq b,\) \(0\leq a\leq x\leq y.\)
- If \(z=f(x)\) is continuous on \(R,\) show that \( \displaystyle\iint\limits_{\kern-3ptR}f(x) \,{\it dA}=\int_{a}^{b}(b-x)f(x)\,{\it dx}\).
Question
Properties of Double Integrals Using properties of double integrals, show that if the functions \(f\) and \(g\) are integrable on \(R\) and \( f(x,y)\leq g(x,y)\) for all \((x,y)\) in \(R\), then \(\displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA} \leq \displaystyle\iint\limits_{\kern-3ptR}g(x,y)\,{\it dA}\).
Challenge Problem
Question
Volume Find the volume of the solid under the graph of the elliptic paraboloid \(z=8-2x^{2}-y^{2}\) and above the first quadrant of the \(xy\)-plane. (Hint: Use Wallis’s formula from Section 7.1, Problem 69.)
