14.3 Assess Your Understanding
Concepts and Vocabulary
Question
Convert the function \(f(x,y) =\sqrt{4x^{2}+4y^{2}}\) to polar coordinates.
Question
In polar coordinates, the differential \({\it dA}\) of area is \(dA\) = _________.
Question
True or False Geometrically, if \(f(x,y)\geq 0\) and if \(f\) is continuous over a closed, bounded region \(R\), then the double integral \( \iint\limits_{\kern-3ptR}f(r\cos\theta, r \sin \theta )\,{dr d\theta}\) represents the volume of the solid under the surface \(z=f(x,y)\) and above the region \(R\) in the \(xy\)-plane.
Question
True or False \(\iint\limits_{\kern-3ptR}r\,dr\,d\theta\) equals the area \(A\) of the closed, bounded region \(R\).
Skill Building
In Problems 5–8, assume that \(z=f(x,y)\) is a continuous function over the region \(R.\) Express the double integral \(\displaystyle\iint\limits_{\displaystyle\kern-3ptR}f(x,y) \, {\it dA}\) over \(R\) as an iterated integral using polar coordinates.
Question

Question
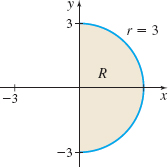
Question
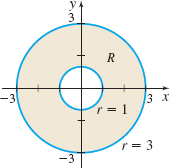
Question
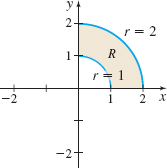
In Problems 9–14, express each double integral over the region \( R\) as an iterated integral using polar coordinates; do not integrate.
Question
\(\iint\limits_{\kern-3ptR} ( x+y) \, {\it dA},\) \(R\) is enclosed by \(x^{2}+y^{2}=9\), \(x\geq 0\), and \(y\geq 0\).
Question
\(\iint\limits_{\kern-3ptR}(x^{2}+y^{2}) \, {\it dA},\) \(R\) is enclosed by \(y=\sqrt{1-x^{2}}\) and the lines \(y=x\) and \(y=-x.\)
Question
\(\iint\limits_{\kern-3ptR}x\, {\it dA},\) \(R\) is enclosed by \(x=\sqrt{4-y^{2}},\) the positive \(x\)-axis, and the line \(y=x.\)
Question
\(\iint\limits_{\kern-3ptR}y\, {\it dA},\) \(R\) is enclosed by \(y=\sqrt{16-x^{2}},\) in the first quadrant.
Question
\(\iint\limits_{\kern-3ptR}( x+y^{2}) \, {\it dA},\) \(R\) is enclosed by \(x^{2}+y^{2}=1\) and \(x^{2}+y^{2}=4\).
Question
\(\iint\limits_{\kern-3ptR}\sqrt{x^{2}+y^{2}}\, {\it dA},\) \(R\) is enclosed by \(x^{2}+y^{2}=\dfrac{1}{4}\) and \(x^{2}+y^{2}=5\).
928
In Problems 15–22, find each iterated integral.
Question
\(\displaystyle\int_{0}^{\pi /4}\int_{0}^{4\sin \theta }r\cos \theta \,{\it dr}\,d\theta \)
Question
\(\displaystyle\int_{0}^{5\pi /3}\int_{0}^{2\cos \theta }r\sin \theta \,{\it dr}\,d\theta \)
Question
\(\displaystyle\int_{0}^{\pi /2}\int_{0}^{\pi /3}r\,\,d\theta\, {\it dr}\)
Question
\(\displaystyle\int_{0}^{\pi /3}\int_{0}^{\sin \theta }r\,{\it dr}\,d\theta \)
Question
\(\displaystyle\int_{0}^{\pi /4}\int_{0}^{\cos \theta }r\,{\it dr}\,d\theta \)
Question
\(\displaystyle\int_{0}^{4}\int_{-\pi /4}^{\pi /4}r\cos \theta \,d\theta\, {\it dr}\)
Question
\(\displaystyle\int_{0}^{2}\int_{-\pi /3}^{5\pi /3}r\sin \theta \,d\theta\, {\it dr} \)
Question
\(\displaystyle\int_{0}^{\pi}\int_{0}^{\pi /4}r\,\,d\theta\, {\it dr}\)
In Problems 23–28, graph the region \(R,\) then find each double integral.
Question
\(\displaystyle\iint\limits_{\kern-3ptR}3\sin \theta \,{\it dA} ,\quad\)\(0\leq r\leq 2,\) \(0\leq \theta \leq \dfrac{\pi }{2}\)
Question
\(\displaystyle\iint\limits_{\kern-3ptR}4\cos \theta \,{\it dA} ,\quad\) \(0\leq r\leq 3,\) \(0\leq \theta \leq \dfrac{\pi }{2}\)
Question
\(\displaystyle\iint\limits_{\kern-3ptR}2r \sin \theta \,{\it dA} ,\quad\) \(0\leq r\leq 1,\) \(0\leq \theta \leq \dfrac{\pi }{2}\)
Question
\(\displaystyle\iint\limits_{\kern-3ptR}3r \cos \theta \,{\it dA} ,\quad\) \(0\leq r\leq 2\), \(0\leq \theta \leq \dfrac{\pi }{4}\)
Question
\(\displaystyle\iint\limits_{\kern-3ptR}3r^{2}\sin \theta \,{\it dA} ,\quad\) \(0\leq r\leq 2,\) \(-\dfrac{\pi }{2}\leq \theta \leq \dfrac{\pi }{2}\)
Question
\(\displaystyle\iint\limits_{\kern-3ptR}2r^{2}\cos \theta \,{\it dA} ,\quad\) \(0\leq r\leq 4,\) \(- \dfrac{\pi }{2}\leq \theta \leq \dfrac{\pi }{2}\)
In Problems 29–42, find each double integral by changing to polar coordinates.
Question
\(\displaystyle\int_{0}^{1}\int_{0}^{\sqrt{1-x^{2}}}\,{\it dy}\,{\it dx}\)
Question
\(\displaystyle\int_{0}^{3}\int_{0}^{y}\sqrt{x^{2}+y^{2}}\,{\it dx}\,{\it dy}\)
Question
\(\displaystyle\int_{-2}^{2}\int_{0}^{\sqrt{4-y^{2}}}(x^{2}+y^{2})\,{\it dx}\,{\it dy}\)
Question
\(\displaystyle\int_{0}^{2}\int_{0}^{\sqrt{4-x^{2}}}\sqrt{4-x^{2}-y^{2}}\, {\it dy}\,{\it dx}\)
Question
\(\displaystyle\int_{0}^{1}\int_{0}^{\sqrt{1-x^{2}}}\cos (x^{2}+y^{2})\,{\it dy}\,{\it dx}\)
Question
\(\displaystyle\int_{0}^{1}\int_{0}^{\sqrt{1-y^{2}}}e^{\sqrt{x^{2}+y^{2}}}\,{\it dx}\,{\it dy}\)
Question
\(\iint\limits_{\kern-3ptR}e^{-(x^{2}+y^{2})}\,d\!A,\) \(R\) is the region in the first quadrant enclosed by the circles \(x^{2}+y^{2}=1\) and \(x^{2}+y^{2}=4\).
Question
\(\displaystyle\iint\limits_{\kern-3ptR}\dfrac{y}{\sqrt{x^{2}+y^{2}}}\,d\!A,\) \(R\) is the region in the first quadrant inside the circle \(x^{2}+y^{2}=a^{2}.\)
Question
\(\iint\limits_{\kern-3ptR}x\,d\!A,\) \(R\) is the region enclosed by the circle \(x^{2}+y^{2}=x\).
Question
\(\iint\limits_{\kern-3ptR}y^{2}\,d\!A,\) \(R\) is the region enclosed by the circle \(x^{2}+y^{2}=2y\).
Question
\(\iint\limits_{\kern-3ptR}\sqrt{x^{2}+y^{2}}\,d\!A,\) \(R\) is the region enclosed by \(r=3+\cos \theta \).
Question
\(\iint\limits_{\kern-3ptR}(x^{2}+y^{2})\,d\!A,\) \(R\) is the region enclosed by \(r=2(1+\sin \theta )\).
Question
\(\displaystyle\int_{-2}^{2}\int_{-\sqrt{4-y^{2}}}^{\sqrt{4-y^{2}} }(x^{2}+y^{2})^2\,{\it dx}\,{\it dy}\)
Question
\(\displaystyle\int_{0}^{2}\int_{\sqrt{2x-x^{2}}}^{\sqrt{4x-x^{2}}}\,{\it dy}\,{\it dx}+\int_{2}^{4}\int_{0}^{\sqrt{ 4x-x^{2}}}\,{\it dy}\,{\it dx}\)
Applications and Extensions
In Problems 43–52, use double integrals in polar coordinates.
Question
Volume Find the volume of the solid enclosed by the ellipsoid \(x^{2}+y^{2}+4z^{2}=4\).
Question
Volume Find the volume of the solid enclosed by the paraboloid \(x^{2}+y^{2}=az\), \(a > 0\), the \(xy\)-plane, and the cylinder \( x^{2}+y^{2}=a^{2}\).
Question
Volume Find the volume of the portion of the ball (a solid sphere) of radius \(4\) and center at the origin that lies above the region enclosed by the circle \(r=4\sin \theta ,\) as shown in the figure below.
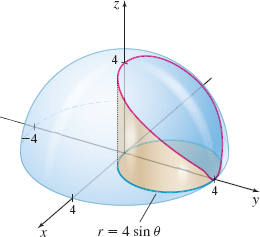
Question
Volume Find the volume of the solid cut from the ellipsoid \( x^{2}+y^{2}+4z^{2}=4\) by the cylinder \(x^{2}+y^{2}=1\).
Question
Area Find the area enclosed by one loop of \(r^{2}=9\sin (2\theta) \).
Question
Area Find the area of the region that lies inside the circle \( r=4\cos \theta \) but outside the circle \(r=\cos \theta \).
Question
Area Find the area of the region in the first quadrant that lies inside the limaçon \(r=3+2\sin \theta \) but outside the circle \(r=4\sin \theta .\) See the figure.

Question
Area Find the area of the region that lies inside the circle \(r=1\) but outside the cardioid \(r=1+\cos \theta \).
Question
Area Find the area of the region that lies inside the cardioid \(r=1+\cos \theta \) but outside the circle \(r=\dfrac{1}{2}\).
929
Question
Area Find the area of the region that lies inside the limaçon \(r=3-\cos \theta \) but outside the circle \(r=5\cos \theta \).
In Problems 53 and 54, replace each iterated integral in polar coordinates with an iterated integral in rectangular coordinates. Do not find the integrals.
Question
\(\displaystyle\int_{0}^{1/\sqrt{2}}\int_{0}^{\sin ^{-1}r}r\,d\theta \,dr\)
Question
\(\displaystyle\int_{0}^{1}\int_{\cos ^{-1}r}^{\pi /2}r^{2}\sin \theta \,d\theta \,dr\)
Question
A tank in the shape of a hemisphere of radius 1 m is lying on its flat side. If the tank is filled with liquid to a depth of \(a\) meters, what is the volume of the liquid? (Hint: Position the hemisphere as shown in the figure.)

Question
Repeat Problem 55 if the tank is configured as in the figure, with its flat side at ground level and its rounded base under the ground.

Question
![]() Area
Area
- Use technology to graph \(r=\theta ,\) \( 0\leq \theta \leq 2\pi .\)
- Find the area of the region enclosed by the graph of \(r=\theta\) and the positive \(x\)-axis.
Question
Volume Find the volume of the solid cut from the sphere \( x^{2}+y^{2}+z^{2}=a^{2}\) by the cylinder \(x^{2}+y^{2}=ay\), \(a\gt 0\).
Question
Area Find the area enclosed by one leaf of the rose \(r=\sin (3\theta) \).
Challenge Problems
Question
- Express \(f(x,y) =\dfrac{{1}}{x^{2} \sqrt{x^{2}+y^{2}}}\,,\) using polar coordinates.
- Find \(\displaystyle\int_{1}^{2}{\int_{0}^{1}} \dfrac{1}{x^{2}\sqrt{x^{2}+y^{2}}}\, {\it dy}\,{\it dx}.\)
Question
To find \(\int_{-\infty }^{\infty }e^{-x^{2}}\,{\it dx}\), let \( I_{a}=\int_{0}^{a}e^{-x^{2}}\,{\it dx}\).
- Show that: \[ I_{a}^{2}=\int_{0}^{a}e^{-x^{2}}\,{\it dx}\int_{0}^{a}e^{-y^{2}} {\it dy}=\int_{0}^{a} \int_{0}^{a}e^{-(x^{2}+y^{2})}\,{\it dx}\,{\it dy} \]
- Let \(J_{a}=\iint\limits_{\kern-3ptR}e^{-(x^{2}+y^{2})}\,{\it dA}\), where \(R\) is the quarter circle \(0\leq \theta \leq \dfrac{\pi }{2}\), \( 0\leq r\leq a\) . Show that \[ \big\vert I_{a}^{2}-J_{a}\big\vert \leq \dfrac{(4-\pi )a^{2}}{4}e^{-a^{2}} \]
- Find \(J_{a}\).
- Show that \[ \lim_{a\rightarrow \infty }J_{a}=\dfrac{\pi }{4}\qquad \hbox{and}\qquad \lim_{a\rightarrow \infty }\,\big\vert \,I_{a}^{2}-J_{a}\big\vert =0 \]
- Show that \(\int_{-\infty }^{\infty }e^{-x^{2}}\,{\it dx}=\sqrt{\pi }\). (This integral is of special importance in statistics.)
