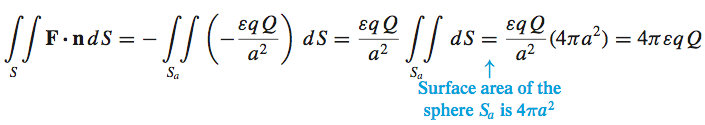15.8 The Divergence Theorem
OBJECTIVES
When you finish this section, you should be able to:
- Find the divergence of a vector field (p. 1038)
- Use the Divergence Theorem (p. 1038)
- Interpret the divergence of \(\mathbf{F}\) (p. 1042)
Green’s Theorem expresses a relationship between a certain double integral over a plane region and a line integral taken around its boundary. There are two ways to generalize this result to space. One of these, known as the Divergence Theorem, is the subject of this section, and the other, known as Stokes’ Theorem, is the subject of the next section.
The Divergence Theorem expresses a certain relationship between a triple integral involving the divergence of a vector field and a surface integral, the flux of a vector field. The theorem is used in applications involving fluid dynamics, electrostatics, and magnetism. We begin with the definition of divergence of a vector field.
1038
spanDEFINITIONspan Divergence of \(\mathbf{F}\)
Let \(\mathbf{F}=\mathbf{F}(x,y,z)=P(x,y,z)\mathbf{i}+Q(x,y,z)\mathbf{j }+R(x,y,z)\mathbf{k}\) be a vector field, where \(\dfrac{\partial P}{ \partial x}\), \(\dfrac{\partial Q}{\partial y}\), and \(\dfrac{\partial R}{ \partial z}\) exist. The divergence of \(\mathbf{F}\), denoted by \(\rm{div}\mathbf{F}\), is defined as the function* \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ {\rm div} \mathbf{F}=\dfrac{\partial P}{ \partial x}+\dfrac{\partial Q}{\partial y}+ \dfrac{\partial R}{\partial z} }} \]
* Some books define \(\rm{div}\mathbf{F}\) as the dot product \({\bf\nabla }\,{\bf\cdot}\, \mathbf{F}\), where \({\bf\nabla }\) is the partial differential operator \({\bf\nabla}=\dfrac{\partial }{\partial x}\mathbf{i}+\dfrac{\partial }{\partial y}\mathbf{j}+ \dfrac{\partial }{\partial z}\mathbf{k}\) and \(\mathbf{F}=P\mathbf{i}+Q\mathbf{j}+R\mathbf{k}\).
1 Find the Divergence of a Vector Field
Finding the Divergence of \(\mathbf{F}\)
The divergence of the vector field \[ \mathbf{F}(x,y,z)=x^{2}yz^{2}\mathbf{i}+(2xz+y^{3})\mathbf{j}+x^{2}y^{3}z \mathbf{k} \]
is \[ {\rm div}\mathbf{F}=\dfrac{\partial }{\partial x}(x^{2}yz^{2})+\dfrac{ \partial }{\partial y}(2xz+y^{3})+\dfrac{\partial }{\partial z} (x^{2}y^{3}z)=2xyz^{2}+3y^{2}+x^{2}y^{3} \]
NOW WORK
Problem 5.
2 Use the Divergence Theorem
The Divergence Theorem (or Gauss’ Theorem) states that if certain conditions are satisfied, a triple integral is equal to the flux of a fluid with constant mass density \(\rho =1\) across a surface; that is, a triple integral can be expressed as a surface integral.

ORIGINS
Although Carl Friedrich Gauss (1777 – 1855) was neither the first to discover nor the first to prove the Divergence Theorem, the theorem is named in honor of him. The Divergence Theorem was proved by the Russian mathematician Mikhail Ostrogradsky (1801 – 1862), whose name is also associated with the theorem. Gauss is considered among the greatest mathematicians of all time. He was the mentor of many other notable mathematicians including Riemann, Bessel, Dedekind, and Möbius.
THEOREM Divergence Theorem
Let \(S\) be a positively oriented surface with outer unit normal \(\mathbf{n}\) that encloses a closed, bounded solid \(E\) in space. Let \(\mathbf{ F}=\mathbf{F}(x,y,z)=P(x,y,z)\mathbf{i}+Q(x,y,z)\mathbf{j}+R(x,y,z)\mathbf{k}\) be a vector field for which the functions \(P\), \(Q\), and \(R\) have continuous first-order partial derivatives on an open set containing \(E\). Then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \iiint\limits_E {{\rm div}}\ \mathbf{F} \,dV=\iiint\limits_S{\mathbf{F}}\,{\cdot}\, \mathbf{n}\,dS }} \]
If \(\mathbf{n}=\cos \alpha \mathbf{i}+\cos \beta \mathbf{j}+\cos \gamma \mathbf{k}\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \iiint\limits_E \left( \dfrac{\partial P}{\partial x}+\dfrac{\partial Q}{ \partial y}+\dfrac{\partial R}{\partial z}\right) dV=\iint\limits_S (P\cos \alpha +Q\cos \beta +R\cos \gamma )\,dS }} \]
The proof of the Divergence Theorem for the general conditions on the solid \(E\) can be found in Advanced Calculus texts. The idea behind the proof is to verify each of the three equations \[ \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \iiint\limits_E \dfrac{\partial P}{\partial x} \,dV=\iint\limits_S P\cos \alpha \,dS }} \end{equation*} \tag{1} \]
1039
\[ \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \iiint\limits_E \dfrac{\partial Q}{\partial y} \,dV=\iint\limits_S Q\cos \beta \,dS }} \end{equation*} \tag{2} \] \[ \begin{equation} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \iiint\limits_E \dfrac{\partial R}{\partial z} \,dV=\iint\limits_S R\cos \gamma \,dS }} \end{equation} \tag{3} \]
Once they are verified, the Divergence Theorem follows by adding the three equations.
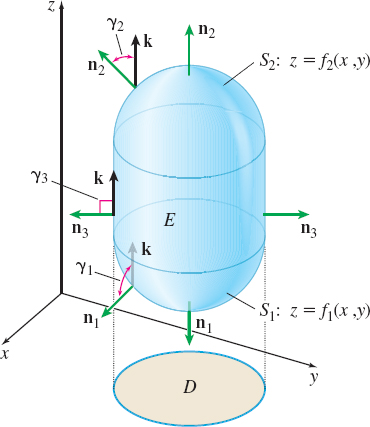
We prove (3) for a special case of the solid \(E\) as described in Example 5 from Section 15.7. As Figure 67 shows, the surface \(S\) that encloses \(E\) is a positively oriented, \(xy\)-simple surface consisting of three surfaces, \(S_{1}\), \(S_{2}\), and \(S_{3}\), with the outer unit normals \(\mathbf{n}_{1}\), \(\mathbf{n}_{2}\), and \(\mathbf{n}_{3}\), respectively.
Proof
We assume that surfaces \(S_{1}\) and \(S_{2}\) are defined by the equations \[ S_{1}{:} \quad z=f_{1}(x,y) \qquad \hbox{and}\qquad S_{2}{:}\quad z=f_{2}(x,y) \]
where \(f_{1}(x,y)<f_{2}(x,y)\) on \(D\), \(f_{1}\) and \(f_{2}\) are continuous on \(D\), and \(f_{1}\) and \(f_{2}\) have continuous partial derivatives on \(D\). The surface \(S_{3}\) is the portion of a cylindrical surface between \(S_{1}\) and \(S_{2}\) formed by lines parallel to the \(z\)-axis and along the boundary of the region \(D\) in the \(xy\)-plane. The solid \(E\) is enclosed on the bottom by \(S_{1}\), on the top by \(S_{2}\), and on the sides by the lateral surface \(S_{3}\).
We now show that \[ \begin{equation} \tag{4} \iiint\limits_E \dfrac{\partial R}{\partial z}\,dV=\iint\limits_S R\cos \gamma \,dS \end{equation} \]
We start with the right side of (4). Then using the fact that \(S\) consists of the three surfaces \(S_{1}\), \(S_{2}\), and \(S_{3}\), we have \[ \iint\limits_S R\cos \gamma \,dS=\iint\limits_{S_{1}}R\cos \gamma \,dS+\iint\limits_{S_{2}}R\cos \gamma \,dS+\iint\limits_{S_{3}}R\cos \gamma \,dS \]
For the bottom surface \(S_{1}\): \(z=f_{1}(x,y)\), the outer unit normal \(\mathbf{n}_{1}\) equals the downward-pointing unit normal vector \(-\mathbf{n}\) to \(S_{1}\). So, \(\cos \gamma\) is given by \[ \cos \gamma =\mathbf{n}_{1}\,{\bf\cdot}\, \mathbf{k}=\dfrac{-1}{\sqrt{ [(f_{1})_x(x,y)]^{2}+[(f_{1})_y(x,y)]^{2}+1}} \] See Example 5 (page 1032).
Then \[ \iint\limits_{S_{1}}R\cos \gamma \,dS=\iint\limits_{S_{1}}R(x,y,f_{1}(x,y)) \dfrac{-1}{\sqrt{[(f_{1})_x(x,y)]^{2}+[(f_{1})_y(x,y)]^{2}+1}}\,dS \]
We can express the surface integral as a double integral \[ \begin{eqnarray} \iint\limits_{S_{1}}R\cos \gamma \,dS&=&-\iint\limits_D R(x,y,f_{1}(x,y)) \dfrac{\sqrt{[(f_{1})_x(x,y)]^{2}+[(f_{1})_y(x,y)]^{2}+1}\,}{\sqrt{ [(f_{1})_x(x,y)]^{2}+[(f_{1})_y(x,y)]^{2}+1}}\,dx\,dy\nonumber \\ &=&-\iint\limits_D R(x,y,f_{1}(x,y))\,dx\,dy \tag{5} \end{eqnarray} \]
For the top surface \(S_{2}\): \(\ z=f_{2}(x,y)\), the outer unit normal \(\mathbf{n}_{2}\) equals the upward-pointing unit normal vector \(\mathbf{n}\) to \(S_{2}\). So, \(\cos \gamma\) is given by \[ \cos \gamma =\mathbf{n}_{2}\,{\bf\cdot}\, \mathbf{k}=\dfrac{1}{\sqrt{ [(f_{2})_x(x,y)]^{2}+[(f_{2})_y(x,y)]^{2}+1}} \]See Example 5 (page 1032).
1040
and \[ \iint\limits_{S_{2}}R\cos \gamma \,dS=\iint\limits_{S_{2}}R(x,y,f_{2}(x,y)) \dfrac{1}{\sqrt{[(f_{2})_x(x,y)]^{2}+[(f_{2})_y(x,y)]^{2}+1}}\,dS \]
Again, we can express the surface integral as a double integral. \[ \begin{eqnarray} \iint\limits_{S_{2}}R\cos \gamma \,dS&=&\iint\limits_{D}R(x,y,f_{2}(x,y))\dfrac{ \sqrt{[(f_{2})_x(x,y)]^{2}+[(f_{2})_y(x,y)]^{2}+1}\,}{\sqrt{ [(f_{2})_x(x,y)]^{2}+[(f_{2})_y(x,y)]^{2}+1}}\,dx\,dy \nonumber \\ &=&\iint\limits_{D}R(x,y,f_{2}(x,y))\,dx\,dy \tag{6} \end{eqnarray} \]
On the lateral surface \(S_{3}\), the angle between \(\mathbf{n}_{3}\) and \(\mathbf{k}\) is \(\gamma =\dfrac{\pi }{2}\), so \(\cos \gamma =0\). Therefore, \[ \begin{equation*} \iint\limits_{\kern-3ptS_{3}}R\cos \gamma \,dS=0 \end{equation*} \tag{7} \]
We now obtain \(\iint\limits_S R\cos \gamma \,dS\) by summing (5), (6), and (7): \[ \begin{eqnarray*} \iint\limits_{S} R\cos \gamma \,dS& =&\iint\limits_{S_{1}}R\cos \gamma \,dS+\iint\limits_{S_{2}}R\cos \gamma \,dS+\iint\limits_{S_{3}}R\cos \gamma \,dS \\ &=&-\iint\limits_{D}R(x,y,f_{1}(x,y))\,dx\,dy+\iint\limits_{D}R(x,y,f_{2}(x,y))\,dx\,dy+0 \\ & =&\iint\limits_{D}[R(x,y,f_{2}(x,y))-R(x,y,f_{1}(x,y))]\,dx\,dy \\ & =&\iint\limits_{D}\left[ \int_{f_{1}(x,y)}^{f_{2}(x,y)}\dfrac{\partial R}{ \partial z}\,dz\right] \,dx\,dy=\iiint\limits_E \dfrac{\partial R}{\partial z }\,dV \end{eqnarray*} \]
which proves (3).
Using the Divergence Theorem to Find Flux
Find the mass of a fluid of constant mass density \(\rho\) flowing across the cube enclosed by the planes \(x=0\), \(x=1\), \(y=0\), \(y=1\), \(z=0\), and \(z=1\) in a unit of time, in the direction of the outer unit normal vectors if the velocity of the fluid at any point on the cube is \(\mathbf{F}=\mathbf{F} (x,y,z)=4xz\mathbf{i}-y^{2}\mathbf{j}+yz\mathbf{k}\). (This is Example 8 on page 1035.)
Solution Suppose \(E\) is the solid cube and \(S\) is its surface. The mass of the fluid is \(\iint\limits_S \rho \mathbf{F}\,{\bf\cdot}\, \mathbf{n} \,dS\), where \(\mathbf{n}\) is the outer unit normal vector of \(S\). Since the velocity of the fluid is \(\mathbf{F}=4xz\mathbf{i}-y^{2}\mathbf{j}+yz\mathbf{ k}\), we have \({\rm{div}}\mathbf{F}=4z-2y+y=4z-y\). Now we use the Divergence Theorem. \[ \begin{eqnarray*} \iint\limits_{S}\rho \mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS &=&\rho \iint\limits_S \mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS=\rho \iiint\limits_E {\rm{div}}\mathbf{F} \,dV=\rho \int_{0}^{1}\int_{0}^{1}\int_{0}^{1}(4z-y)\,dz\,dy\,dx \\ &=&\rho \int_{0}^{1}\int_{0}^{1}(2-y)\,dy\,dx=\rho \int_{0}^{1}\dfrac{3}{2} \,dx=\dfrac{3}{2}\rho \end{eqnarray*} \]
which is the same as the result found in Example 8, Section 15.7.
NOW WORK
Problem 9.
1041
NEED TO REVIEW?
Triple integrals using cylindrical coordinates are discussed in Section 14.7, pp. 950-954.
Using the Divergence Theorem to Find a Surface Integral
Let \(S\) be the surface of a cylindrical solid \(E\) whose boundary is \(x^{2}+y^{2}=4\), \(z=0\), and \(z=1\). Let \(\mathbf{F}=x^{3}\mathbf{i}+y^{3} \mathbf{j}+z^{2}\mathbf{k}\) and let \(\mathbf{n}\) be the outer unit normal to \(S\). Use the Divergence Theorem to find \(\iint\limits_S \mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS\).
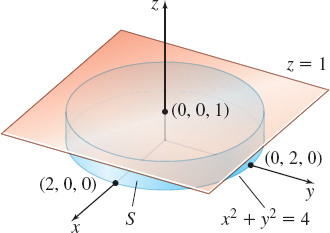
Solution Figure 68 illustrates the cylindrical surface \(S\). We begin by finding \({\rm{div}}\mathbf{F}=3x^{2}+3y^{2}+2z\). Then we use the Divergence Theorem, obtaining \[ \iint\limits_{S}\mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS=\iiint \limits_{E}(3x^{2}+3y^{2}+2z)\,dV \]
Because \(E\) is a cylindrical solid, we use cylindrical coordinates: \[ 3x^{2}+3y^{2}+2z=3r^{2}\cos ^{2}\theta +3r^{2}\sin ^{2}\theta+ 2z=3r^{2}( \cos ^{2}\theta +\sin ^{2}\theta ) +2z=3r^{2}+2z \]
The solid \(E\) is given by \(0\leq r\leq 2\), \(0\leq \theta \leq 2\pi\) , \(0\leq z\leq 1\). Then \[ \begin{eqnarray*} \iint\limits_{S}\mathbf{F}\,{\cdot}\, \mathbf{n}\,ds& =&\iiint\limits_E(3x^{2}+3y^{2}+2z)\,dV \underset{\underset{\color{#0066A7}{dV=r\,dr\,d\theta \,dz}}{\color{#0066A7}{\uparrow}}} {=} \iiint\limits_E(3r^{2}+2z)\,r\,dr\,d\theta dz \\ &=&\int_{0}^{2\pi }\int_{0}^{2}\int_{0}^{1}(3r^{3}+2rz)\,dz\,dr\,d\theta \\ & =&\int_{0}^{2\pi }\int_{0}^{2}\big[ 3r^{3}z+r z^{2}\big] _{0}^{1}\,dr\,d\theta =\int_{0}^{2\pi }\int_{0}^{2}(3r^{3}+r)\,dr\,d\theta\\ &=&\int_{0}^{2\pi }\left[ \dfrac{3r^{4}}{4}+\dfrac{r^{2}}{2}\right] _{0}^{2}\,d\theta =\int_{0}^{2\pi }14\,d\theta =28\pi \end{eqnarray*} \]
NOW WORK
Problem 13.
Using the Divergence Theorem to Find a Surface Integral
Let \(\mathbf{F}(x,y,z)=x^{3}\mathbf{i}+y^{3}\mathbf{j}+z^{3}\mathbf{k}\). If \(S\) is the surface of the spherical solid \(E\) in the first octant enclosed by \(z=\sqrt{ 4-x^{2}-y^{2}}\) and \(z=0\), and \(\mathbf{n}\) is the outer unit normal to \(S\), use the Divergence Theorem to find \(\iint\limits_S \mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS\).
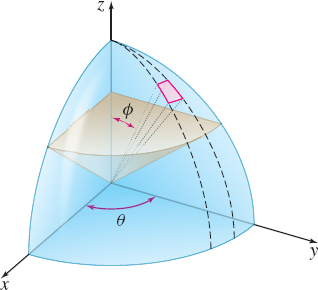
Solution See Figure 69. Since \({\rm{div}}\mathbf{F} =3x^{2}+3y^{2}+3z^{2}=3(x^{2}+y^{2}+z^{2})\), we use the Divergence Theorem, obtaining \[ \iint\limits_{S}\mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS=3\iiint \limits_E(x^{2}+y^{2}+z^{2})\,dV \]
We use spherical coordinates to find the triple integral. Then \(x^{2}+y^{2}+z^{2}=\rho ^{2}\) and \(dV=\rho ^{2}\sin \phi \,d\rho \,d\theta \,d\phi\). The solid \(E\) is given by \(0\leq \rho \leq 2\), \(0\leq \theta \leq \dfrac{\pi}{2}\), \(0\leq \phi \leq \dfrac{\pi }{2}\). Then \[ \begin{eqnarray*} \iint\limits_{S}\mathbf{F}\,{\cdot}\, \mathbf{n}\,dS &= &3\iiint\limits_E \rho ^{2}( \rho ^{2}\sin \phi \,d\rho \,d\theta \,d\phi ) = 3\int_{0}^{\pi /2}\int_{0}^{\pi /2 }\int_{0}^{2}\rho ^{4}\,\sin \phi \,d\rho \,d\theta \,d\phi \notag \\ &=&3\int_{0}^{\pi /2}\int_{0}^{\pi /2}\left[ \dfrac{\rho ^{5}}{5}\right] _{0}^{2}\sin \phi\, d\theta \,d\phi =3\int_{0}^{\pi /2}\int_{0}^{\pi /2 }\dfrac{ 32}{5}\sin \phi\, d\theta \,d\phi \\ &=&\dfrac{96}{5}\int_{0}^{\pi /2}\big[ \theta \big] _{0}^{\pi /2}\sin \phi \,d\phi \notag \\ &=&\dfrac{48\pi }{5}\int_{0}^{\pi /2}\sin \phi \,d\phi =\dfrac{48\pi }{5} \big[ -\cos \phi \big] _{0}^{\pi /2}=\dfrac{48\pi }{5} \end{eqnarray*} \]
NEED TO REVIEW?
Triple integrals using spherical coordinates are discussed in Section 14.8, pp. 956-960.
NOW WORK
Problem 15.
3 Interpret the Divergence of F
1042
NEED TO REVIEW?
The Mean Value Theorem for integrals is discussed in Section 5.4, pp. 372-374.
Recall that the Mean Value Theorem for single integrals states that if a function \(f\) of one variable is continuous on a closed interval \([a,b]\), then there is a real number \(u\), \(a\leq u\leq b\), for which \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{a}^{b}f(x)\,dx=f(u)(b-a) }} \]
Similarly, there is a Mean Value Theorem for triple integrals asserting that if a function \(f\) of three variables is continuous in a simply connected, closed, bounded solid \(E\), then there is a point \((x^{\ast },y^{\ast },z^{\ast })\) in \(E\) for which \[ \tag{8} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \iiint\limits_Ef(x,y,z)\,dV=f(x^{\ast },y^{\ast },z^{\ast})V }} \]
where \(V\) is the volume of \(E \).
Let \(\mathbf{F}=\mathbf{F}(x,y,z)\) be a vector field defined and continuous on and within a spherical solid \(E_{a}\) of radius \(a\) with its center at \((x_{1},y_{1},z_{1})\). Based on (8), there is a point \((x^{\ast },y^{\ast },z^{\ast })\) in \(E_{a}\) for which \[ \begin{equation*} \iiint\limits_{E_{a}}{\rm{div}}\mathbf{F}\,dV_{a}={\rm{div}}\mathbf{F} (x^{\ast },y^{\ast },z^{\ast })V_{a} \end{equation*} \]
where \(V_{a}\) is the volume of the sphere of radius \(a\). Now we use the Divergence Theorem to obtain \[ \iiint\limits_{E_{a}}{\rm{div}}\mathbf{F}\,dV_{a}=\iint\limits_{S_{a}} \mathbf{F}\,{\cdot}\, \mathbf{n}\,dS_{a} \]
where \(S_{a}\) is the sphere of radius \(a\) with its center at \((x_{1},y_{1},z_{1})\). Combining these last two equations, we get \[ {\rm{div}}\mathbf{F}(x^{\ast },y^{\ast },z^{\ast })=\dfrac{ \iint\limits_{S_{a}}\mathbf{F}\,{\cdot}\, \mathbf{n}\,dS_{a}}{V_{a}} \]
The ratio on the right side is the flux of \(\mathbf{F}\) per unit volume across \(S_{a}\). If we let the radius \(a\rightarrow 0\), then \((x^{\ast },y^{\ast },z^{\ast })\rightarrow (x_{1},y_{1},z_{1})\), so that \[ \tag{9} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ {\rm{div}}\mathbf{F}(x_{1},y_{1},z_{1})=\lim\limits_{a \rightarrow 0}\left( \dfrac{\iint\limits_{S_{a}}\mathbf{F}\,{\cdot}\, \mathbf{n} \,dS_{a}}{V_{a}}\right) }} \]
In other words, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ {\rm{div}}\mathbf{F}(x_{1},y_{1},z_{1})= \hbox{ Limiting value of the flux of \(\mathbf{F}\) per unit volume across \(S_{a}\)} }} \]
If \(\mathbf{F}\) is the velocity of a steady fluid flow and if \({\rm{div}} \mathbf{F}(x_{1},y_{1},z_{1})>0\), then the net flow is out of \(S_{a}\) and the point \((x_{1},y_{1},z_{1})\) is called a source. If \({\rm{div}} \mathbf{F}(x_{1},y_{1},z_{1})<0\), then the net flow is into \(S_{a}\) and the point \((x_{1},y_{1},z_{1})\) is called a sink. In terms of this vocabulary, the Divergence Theorem states that the net flow through \(S_{a}\) equals the sum of the sources and sinks across \(S_{a}\).
If there are no sources or sinks across \(S\), then \({\rm{div}}\mathbf{F}=0\), and we call \(\mathbf{F}\) a solenoidal vector field. For such fields, \[ {\rm{div}}\mathbf{F}=\dfrac{\partial P}{\partial x}+\dfrac{\partial Q}{ \partial y}+\dfrac{\partial R}{\partial z}=0 \]
is referred to as the equation of continuity.
1043
We close this section with an example of Coulomb’s law of electrostatic attraction, an important law in the study of electrostatic fields,
Applying the Divergence Theorem to an Electric Force Field
Let \(\mathbf{F}=\mathbf{F}(x,y,z)\) be an electric force field \[ \mathbf{F}=\mathbf{F}(x,y,z)=\frac{\varepsilon qQ}{x^{2}+y^{2}+z^{2}}\mathbf{u} \]
where \(\varepsilon \) is a constant that depends on the units used; \(q\) and \(Q \) are the charges of two objects, one located at the point \((0,0,0)\) and the other at a point \((x,y,z)\); and \(\mathbf{u}\) is the unit vector in the direction from \((0,0,0)\) to \((x,y,z)\). Let \(S\) be a closed surface with positive orientation that encloses a solid \(E \) in space.
Show that the following statements are true under the assumptions of the Divergence Theorem:
- If neither \(S\) nor its interior contains the point \((0,0,0)\), then \(\iint\limits_S \mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS=0\). That is, the flux of \(\mathbf{F}\) across \(S\) equals \(0\).
- If the interior of \(S\) contains the point \((0,0,0)\), then \(\iint\limits_S \mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS=4\pi \varepsilon qQ\). That is, the flux of \(\mathbf{F}\) across \(S\) equals \(4\pi \varepsilon qQ\).
Solution The unit vector \(\mathbf{u}=\dfrac{x\mathbf{i}+y\mathbf{j }+z\mathbf{k}}{\sqrt{x^{2}+y^{2}+z^{2}}}\), so that \[ \mathbf{F}=\mathbf{F}(x,y,z)=\varepsilon qQ\dfrac{x\mathbf{i}+y\mathbf{j}+z \mathbf{k}}{(x^{2}+y^{2}+z^{2})^{3/2}} \]
The electric force field \(\mathbf{F}\) is continuous everywhere except at the point \((0,0,0)\).
(a) The surface \(S\) that forms the boundary of the solid \(E \) satisfies the assumptions of the Divergence Theorem. We find \({\rm{div}} \mathbf{F}\). \[ \begin{eqnarray*} {\rm{div}}\mathbf{F}&= &\varepsilon qQ\left\{\dfrac{\partial }{\partial x}\left[ \dfrac{x}{ (x^{2}+y^{2}+z^{2})^{3/2}}\right] +\dfrac{\partial }{\partial y}\left[ \dfrac{y }{(x^{2}+y^{2}+z^{2})^{3/2}}\right] +\dfrac{\partial }{\partial z}\left[ \dfrac{z}{(x^{2}+y^{2}+z^{2})^{3/2}}\right] \right\} \\ &=&\varepsilon qQ\bigg\{\dfrac{(x^{2}+y^{2}+z^{2})^{3/2}-3x^{2} \sqrt{x^{2}+y^{2}+z^{2}}}{(x^{2}+y^{2}+z^{2})^{3}}+\dfrac{ (x^{2}+y^{2}+z^{2})^{3/2}-3y^{2}\sqrt{x^{2}+y^{2}+z^{2}}}{ (x^{2}+y^{2}+z^{2})^{3}} \\ &&+\,\dfrac{(x^{2}+y^{2}+z^{2})^{3/2}-3z^{2}\sqrt{x^{2}+y^{2}+z^{2}}}{ (x^{2}+y^{2}+z^{2})^{3}} \bigg\} \\ &=&\varepsilon qQ\dfrac{3(x^{2}+y^{2}+z^{2})^{3/2}-3\sqrt{x^{2}+y^{2}+z^{2}}(x^{2}+y^{2}+z^{2})}{(x^{2}+y^{2}+z^{2})^{3}}=0 \end{eqnarray*} \]
Therefore, by the Divergence Theorem, \[ \iint\limits_{S}\mathbf{F}\,{\cdot}\, \mathbf{n}\,dS=\iiint\limits_E {\rm{div}} \mathbf{F}\,dV=0 \]

(b) Since the interior of \(S\) contains the origin, \(\mathbf{F}\) is not continuous at the origin, so we cannot use the Divergence Theorem. We use the following argument to prove (b). Let \(E \) be the closed solid enclosed by two separate surfaces: the surface \(S\) and a sphere \(S_{a}\) of radius \(a\), with its center at \((0,0,0)\), as shown in Figure 70. The outer surface is \(S\) and the inner surface is \(S_{a}\). Now \(\mathbf{F}\) is continuous throughout \(E\), so the Divergence Theorem can be used. \[ \iiint\limits_E {\rm{div}}\mathbf{F}\,dV=\iint\limits_{S}\mathbf{F}\,{\cdot}\, \mathbf{n}\,dS+\iint\limits_{S_{a}}\mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS \]
1044
From (a), we know that \(\iiint\limits_{E}{\rm{div}}\mathbf{F}\,dV=0\). So, \[ \iint\limits_{S}\mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS=-\iint\limits_{S_{a}}\mathbf{F }\,{\bf\cdot}\, \mathbf{n}\,dS \]
On the inner surface \(S_{a}\), a sphere of radius \(a\), the outer unit normal is \[ \mathbf{n}=-\dfrac{x\mathbf{i}+y\mathbf{j}+z\mathbf{k}}{a}=-\dfrac{x\mathbf{i}+ y\mathbf{j}+z\mathbf{k}}{\sqrt{x^{2}+y^{2}+z^{2}}} \]
Then \[ \begin{eqnarray*} \mathbf{F}\,{\bf\cdot}\, \mathbf{n\,} &=&\dfrac{\varepsilon qQ}{x^{2}+y^{2}+z^{2}} \mathbf{u}\,{\bf\cdot}\, \left( -\dfrac{x\mathbf{i}+y\mathbf{j}+z\mathbf{k}}{\sqrt{ x^{2}+y^{2}+z^{2}}}\right)\\ &=&-\dfrac{\varepsilon qQ}{x^{2}+y^{2}+z^{2}}\dfrac{x \mathbf{i}+y\mathbf{j}+z\mathbf{k}}{\sqrt{x^{2}+y^{2}+z^{2}}}\,{\bf\cdot}\, \dfrac{x \mathbf{i}+y\mathbf{j}+z\mathbf{k}}{\sqrt{x^{2}+y^{2}+z^{2}}} \\ &=&-\varepsilon qQ\dfrac{x^{2}+y^{2}+z^{2}}{a^{4}}=-\dfrac{\varepsilon qQ}{ a^{2}} \end{eqnarray*} \]
So,