15.2 Line Integrals
OBJECTIVES
When you finish this section, you should be able to:
- Define a line integral in the plane (p. 977)
- Find the value of a line integral along a smooth curve (p. 979)
- Find line integrals of the form \(\boldsymbol\int_{\!\scriptsize\boldsymbol C}~\boldsymbol{f(x}, \boldsymbol{y)}\, \boldsymbol{dx}\) and \(\boldsymbol\int_{\!\scriptsize\boldsymbol C}~\boldsymbol{f(x}, \boldsymbol{y)}\, \boldsymbol{dy}\) (p. 981)
- Find line integrals along a piecewise-smooth curve (p. 984)
- Find the value of a line integral in space (p. 985)
NEED TO REVIEW?
Smooth curves are discussed in Section 9.2, pp. 647-648.
The value of a definite integral \(\int_{a}^{b}f(x)\,dx\) is determined by the values of the function \(f\) on the closed interval \([a,b]\). (See Chapter 5.) The value of a double integral \(\iint\limits_{\kern-3ptR}f(x,y)\,dA\) is determined by the values of \(f\) on a closed, bounded region \(R\) of the \(xy\)-plane, and the value of a triple integral \(\iiint\limits_{\kern-13ptE}f(x,y,z)\,dV\) is determined by the values of \(f\) on a closed, bounded solid \(E\) in space. (See Chapter 14.)
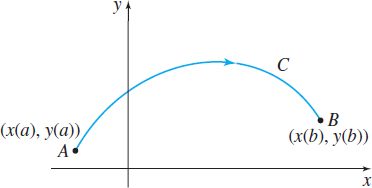
In this section, we define a line integral. The value of a line integral is determined by the values of a function \(f\) along a smooth curve \(C\). A physical application that uses a line integral is the problem of finding the mass of a long thin piece of wire of variable density, whose shape is described by a curve \(C.\)
1 Define a Line Integral in the Plane
Let \(C\) be a smooth curve whose parametric equations are given by \[ x=x(t)\quad y=y(t)\qquad a\leq t\leq b \]
See Figure 10. As \(t\) increases from \(a\) to \(b\), the corresponding points \((x(t),y(t))\) trace out the curve \(C\) from the point \(A=( x(a),y(a)) \) to the point \(B=(x(b),y(b))\); that is, the orientation of \(C\) is from \(A\) to \(B\). Let \(z= f(x,y)\) be a function that is defined on some region containing the curve \(C\).
978
We partition the closed interval \([a,b]\) into \(n\) subintervals: \[ \lbrack a,t_{1}],\quad \lbrack t_{1},t_{2}],\quad \ldots ,\quad \lbrack t_{i-1},t_{i}],\quad \ldots ,\quad \lbrack t_{n-1},b] \]
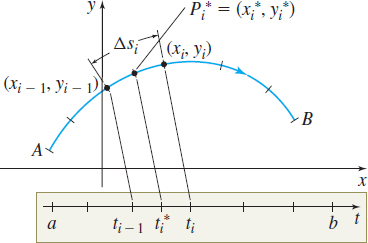
and denote the length of each subinterval by \(\Delta t_{1}\), \(\Delta t_{2}, \ldots ,\Delta t_{i},\ldots , \Delta t_{n}\). Then corresponding to each number \(a=t_{0},\) \(t_{1}, \ldots ,t_{i},\ldots , t_{n}=b\) of the partition, there is a succession of points \(P_{0}\), \(P_{1}, \ldots ,P_{i},\ldots , P_{n}\) on the curve \(C\). These points partition the curve \(C\) into \(n\) subarcs of lengths \(\Delta s_{1}\), \(\Delta s_{2}\), \(\Delta s_{3}, \ldots ,\Delta s_{i},\ldots , \Delta s_{n}\), as shown in Figure 11. We define the norm \(\Vert \Delta \Vert \) of the partition to be the length of the subarc with the largest arc length.
Now we pick a number \(t_{i}{}^*\) in each subinterval \([ t_{i-1},t_{i}]\), \(i=1,2,\ldots ,n,\) and let \(P_{i}{}^*=( x_{i}{}^{*}, y_{i}{}^{*}) \) be the point in the \(i\)th subarc corresponding to the number \(t_{i}{}^*\). We form the sums \[ \sum_{i=1}^{n}f(x_{i}^{\ast },y_{i}^{\ast })\Delta s_{i} \]
These sums depend on both the choice of the partition of \([a,b] \) and the choice of \(P_{i}^{\ast }\). If all such sums can be made as close as we please to a number \(L\) by choosing partitions whose norms are sufficiently close to \(0\), then \(L\) is the limit of these sums as \(\Vert \Delta \Vert \) approaches \(0\) and we write \(L=\lim\limits_{\left\Vert \Delta \right\Vert \rightarrow 0}\sum\limits_{i=1}^{n}f(x_{i}^{\ast },y_{i}^{\ast })\Delta s_{i}.\)
spanDEFINITIONspan Line Integral of \(f\) Along \(C\)
Let \(C\) be a smooth curve defined by the parametric equations \(x=x(t)\) and \(y=y(t)\), \(a\leq t\leq b\). Let \(z=f(x,y)\) be a function defined on some region containing \(C\). The line integral of \(f\) along \(C\) from \(t=a\) to \(t=b\) is \[ {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y)\,ds=\lim\limits_{\Vert \Delta \Vert \rightarrow 0}\sum\limits_{i=1}^{n}f(x_{i}^{\ast },y_{i}^{\ast })\Delta s_{i} }}} \]
provided this limit exists.

The line integral \(\int_{C}f(x,y)\, ds\) is the sum of the values of \(z=f(x,y) \) as \(C\) is traversed from \(t=a\) to \(t=b.\) See Figure 12.
We state without proof a method for finding the value of a line integral when the function \(f\) is continuous on some region that contains \(C\).
THEOREM The Value of a Line Integral
Let \(C\) be a smooth curve defined by the parametric equations \[ x=x(t)\quad y=y(t)\qquad a\leq t\leq b \]
Let \(z=f(x,y)\) be a function that is continuous on some region that contains the curve \(C\). Then the line integral of \(f\) along \(C\) from \(t=a\) to \(t=b\) exists and \[ \begin{equation*} {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y,z)\,ds=\int_{a}^{b}f(x(t),y(t))\sqrt{\left( \dfrac{dx}{dt}\right) ^{\!\!2}+\left( \dfrac{dy}{dt} \right) ^{\!\!2}}dt }}} \tag{1} \end{equation*} \]
NOTE
If \(f(x,y) =1\), the line integral of \(f\) along \(C\) is the arc length of \(C\) from \(t=a\) to \(t=b\).
Equation (1) is the result of substituting the parametric equations \(x=x(t)\) and \(y=y(t)\) of \(C\) for \(x\) and \(y\) in \(f\) and using the arc length formula for the differential \(ds.\) This result expresses the fact that when a function is continuous on a region containing a smooth curve, then the line integral can be found using techniques for finding definite integrals.
NEED TO REVIEW?
Arc length is discussed in Section 9.2, pp. 651-653.
2 Find the Value of a Line Integral Along a Smooth Curve
979
Finding the Value of a Line Integral Along a Smooth Curve
Find \(\int_{C}y\,ds\) if \(C\) is the curve defined by the parametric equations \(x(t)=t\) and \(y(t)=\sqrt{t}\), \(2\leq t\leq 6\)
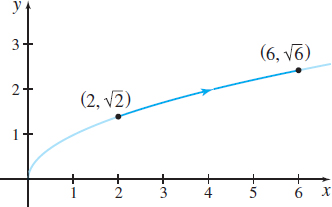
Solution The curve \(C\) is smooth and is part of the graph of \(y=\sqrt{x}\), from \((2,\sqrt{2})\) to \((6,\sqrt{6})\), as shown in Figure 13.
The differential \(ds\) of arc length along \(C\) is given by \[ ds=\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}\,dt \]
Since \(\dfrac{dx}{dt}=1\) and \(\dfrac{dy}{dt}=\dfrac{1}{2\sqrt{t}},\) we have \[ ds=\sqrt{1^{2}+\left( \dfrac{1}{2\sqrt{t}}\right) ^{2}}\,dt=\sqrt{1+\dfrac{1}{4t}}\,dt=\sqrt{\dfrac{4t+1}{4t}}\,dt=\dfrac{\sqrt{4t+1}}{2\sqrt{t}}\,dt \]
Now we use formula (1). \[ \int_{C}y\,ds\underset{\underset{\color{#0066A7}{\hbox{\(y=\sqrt{t}\)}}}{\color{#0066A7}{\uparrow}}}{=}\int_{2}^{6}\sqrt{t}\dfrac{\sqrt{4t+1}}{2\sqrt{t}}\,dt=\dfrac{1}{2}\int_{2}^{6}\sqrt{4t+1}\,dt=\dfrac{1}{2}\left[ \dfrac{(4t+1)^{3/2}}{4\,{\cdot}\, \dfrac{3}{2}}\right] _{2}^{6}=\dfrac{49}{6} \]
NOW WORK
Problem 9.
It can be shown that the value of the line integral along a smooth curve \(C\) does not depend on the parametric representation of the curve; any pair of parametric equations with the same orientation satisfying the assumptions of the Value of a Line Integral Theorem will give the same value.
Finding the Value of a Line Integral
Find \[ \int_{C}(x^{2}+y)\,ds \]
if \(C\) is the line segment from \((0,0)\) to \((1,2)\) and \(C\) is expressed using the parametric equations:
- \(x(t) =t\) and \(y(t) =2t,\quad 0\leq t\leq 1\)
- \(x(t) =\sin t\) and \(y(t) =2\sin t,\quad 0\leq t\leq \dfrac{\pi }{2}\)

Solution The two sets of parametric equations in (a) and (b) are just different ways of representing a part of the line \(y=2x\) from \((0,0)\) to \((1,2)\), as shown in Figure 14.
(a) For \(x(t) =t\) and \(y(t) =2t,\) we have \(\dfrac{dx}{dt}=1\) and \(\dfrac{dy}{dt}=2\). The differential \(ds\) of the arc length \(s\) is \(ds=\sqrt{1^{2}+2^{2}}dt=\sqrt{5}\,dt\). Then \[ \int_{C}(x^{2}+y)\,ds \underset{ \underset{ \underset{\color{#0066A7} {\hbox{\(y=2t\)}}} {\color{#0066A7}{\hbox{\(x=t\)}}}} {\color{#0066A7}{\uparrow }}} {=} \int_{0}^{1}(t^{2}+2t)\sqrt{5}\,dt=\left[\sqrt{5}\left( \dfrac{t^{3}}{3} +t^{2}\right) \right] _{0}^{1}=\dfrac{4\sqrt{5}}{3} \]
980
(b) For \(x(t) =\sin t\) and \(y(t) =2\sin t,\) we have \(\dfrac{dx}{dt}=\cos t\) and \(\dfrac{dy}{dt}=2\cos t\). Since \(\cos t\geq 0\) on \(0\leq t\leq \dfrac{\pi }{2},\) the differential \(ds\) of the arc length \(s\) is \[ ds=\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}} \,dt=\sqrt{\cos ^{2}t+4\cos ^{2}t}\,dt=\sqrt{5\cos ^{2}t}\,dt=\sqrt{5}\cos t\,dt \]
Then \[ \begin{eqnarray*} \int_{C}(x^{2}+y)\,ds \underset{\underset{\underset{\color{#0066A7}{\hbox{\(y=2\sin t\)}}}{\color{#0066A7}{\hbox{\(x=\sin t\)}}}} {\color{#0066A7}{\uparrow }}}{=}\int_{0}^{\pi /2}(\sin ^{2}t+2\sin t)\sqrt{5}\cos t\,dt= \sqrt{5}\int_{0}^{\pi /2}(\sin ^{2}t+2\sin t)\cos t\,dt \\[-10pt] =\sqrt{5}\left[ \dfrac{\sin ^{3}t}{3}+\sin ^{2}t\right] _{0}^{\pi /2}=\dfrac{4\sqrt{5}}{3} \end{eqnarray*} \]
the same value found in (a).
NOW WORK
Problem 21.

The mass of a long thin wire of variable density, whose shape is described by a smooth curve \(C,\) can be found using a line integral. Suppose \(C\) is a smooth curve defined by the parametric equations \(x=x(t) \), \(y=y(t) ,\) for \(a\leq t\leq b.\) Suppose the variable mass density (mass per unit length) at the point \((x,y) \) on \(C\) is \(\rho =\rho (x,y) \), where \(\rho \) is continuous on some region containing \(C.\) We partition \([a,b] \) into \(n\) subintervals \([ t_{i-1},t_{i}] \), for \(i=1,2,\ldots ,n.\) In each subinterval \([ t_{i-1},t_{i}] \), we choose a number \(t_{i}{}^*\), as shown in Figure 15. Then the mass \(\Delta M_{i}\) of the corresponding short piece of wire between \(( x_{i-1},y_{i-1}) \) and \((x_{i}, y_{i}) \) is \(\Delta M_{i}\approx \rho ( x_{i}{}^{*},y_{i}{}^{*}) \Delta s_{i}\), where \(\Delta s_{i}\) is the length of the short piece of wire and \(( x_{i}{}^{*},y_{i}{}^{*}) \) is the point corresponding to \(t_{i}{}^*\). We define the norm \(\Vert \Delta \Vert \) of the partition to be largest length \(\Delta s_{i}\). The sums \[ {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sum\limits_{i=1}^{n} \Delta M_i= \sum\limits_{i=1}^{n}\rho (x_{i}^{\ast },y_{i}^{\ast })\Delta s_{i} }}} \]
over all the subintervals approximate the mass \(M\) of the wire. By taking the limit of these sums as the norm \(\Vert \Delta \Vert \) approaches \(0\), we obtain the mass \(M\) of the wire \[ \begin{equation*} {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ M=\int_{C}\rho (x,y)\,ds }}} \tag{2} \end{equation*} \]
Finding the Mass of a Wire with Variable Density
Find the mass \(M\) of a thin piece of wire in the shape of a semicircle \(x=2\cos t\), \(y=2\sin t\), \(0\leq t\leq \pi \), if the variable density of the wire is \(\rho (x,y)=y+2\).
Solution Using (2), we find that the mass \(M\) of the wire is \[ \begin{eqnarray*} M&=&\int_{C}\rho (x,y)\,ds=\int_{C}(y+2)\,ds=\int_{0}^{\pi }(y+2) \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}dt\\[4pt] &=& \int_{0}^{\pi }(2\sin t+2)\sqrt{(-2\sin t)^{2}+(2\cos t)^{2}}\,dt \hspace{1.5pc}\color{#0066A7}{\dfrac{dx}{dt} =-2\sin t; \dfrac{dy}{dt} =2 \cos t}\\ &=&\int_{0}^{\pi }4(\sin t+1) \,dt=4\big[-\cos t+t\big]_{0}^{\pi }=4[\pi +2] \end{eqnarray*} \]
NOW WORK
Problem 67.
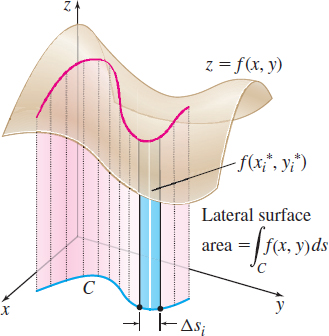
Line integrals also have a geometric application. In Figure 16, the surface \(z=f(x,y) \) lies above the \(xy\)-plane, so \(f(x,y) \geq 0.\) Suppose \(C\) is a smooth curve that lies in the \(xy\)-plane within the domain of \(f.\) If we draw lines parallel to the \(z\)-axis, from \(C\) to the surface, the result is a cylinder, and its area is called the lateral surface area of the cylinder.
981
Finding the Lateral Surface Area of a Cylinder
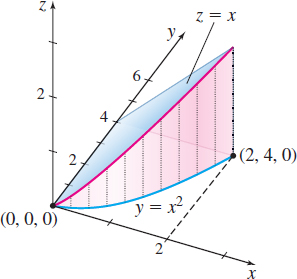
Find the lateral surface area \(A\) of the cylinder that lies above the \(xy\)-plane, below the surface \(z = f(x,y)=x,\) and formed by lines parallel to the \(z\) -axis that intersect the curve \(y=x^{2}\), \(0\leq x\leq 2\).
Solution Figure 17 illustrates the cylinder. Along \(C\), \(y=x^{2},\) the differential \(ds\) of arc length is \[ ds=\sqrt{1+\left( \dfrac{dy}{dx}\right) ^{2}}\,dx\underset{ \underset{\color{#0066A7} {\hbox{\(\dfrac{dy}{dx}=2x\)}}} {\color{#0066A7}{\uparrow }}}{=} \sqrt{1+4x^{2}}\,dx\\[-11pt] \]
The lateral surface area \(A\) of the cylinder is \[ \begin{eqnarray*} A& =&\int_{C}f(x,y) ds=\int_{C}x\,ds=\int_{0}^{2}x\sqrt{1+4x^{2}} \,dx \qquad \color{#0066A7}{{\rm Let}\ u=1+4x^{2};\ {\rm then}\ du=8x\,dx\ {\rm or} \ x\,dx= \dfrac{1}{8}\, du.}\\ && \hspace{14.5pc}\color{#0066A7}{\hbox{When \(x=0\), \(u=1\); when \(x=2\), \(u=17\).}} \\ & =&\int_{1}^{17}\dfrac{1}{8}\sqrt{u}\,du=\left[ \dfrac{1}{4}\dfrac{u^{3/2}}{3}\right] _{1}^{17}=\dfrac{17\sqrt{17}-1}{12} \end{eqnarray*} \]
NOW WORK
Problem 55.
3 Find Line Integrals of the Form ∫Cf(x,y) dx and ∫Cf(x,y) dy
Consider a function \(f\) of two variables \(x\) and \(y\). When we introduced partial derivatives, we said that the partial derivative \(f_{x}(x,y) \) of a function \(z=f(x,y) \) is found by treating \(y\) as a constant \((\Delta y=0) \) and differentiating \(z=f(x,y) \) with respect to \(x;\) similarly, \(f_{y}(x,y) \) is found by holding \(x\) fixed \((\Delta x=0) \) and differentiating \(f \) with respect to \(y.\)
For a line integral \(\int_{C}f(x,y)\, ds,\) the differential \(ds\) of arc length along the smooth curve \(C\) is \((ds) ^{2}=(dx) ^{2}+(dy) ^{2}.\) If we treat \(y\) as a constant, then \(dy=0,\) \(ds=dx,\) and we have the line integral along \(C\) with respect to \(x,\) \(\int_{C}f(x,y)\, dx.\) Similarly, if \(x\) is treated as a constant, then \(dx=0,\) \(ds=dy,\) and we have the line integral along \(C\) with respect to \(y,\) \(\int_{C}f(x,y)\, dy.\)
These line integrals can be expressed as definite integrals if \(C\) is a smooth curve and if the function \(f\) is continuous on a region that contains \(C.\)
THEOREM The Value of a Line Integral Along \(C\) with Respect to \(x\) or \(y\)
Let \(C\) be a smooth curve defined by the parametric equations \[\begin{equation*} x=x(t)\quad y=y(t)\qquad a\leq t\leq b \end{equation*}\]
Let \(f=f(x,y)\) be a function that is continuous on some region that contains the curve \(C\). Then the line integral of \(f\) along \(C\) with respect to \(x\) is given by \[ \begin{equation*} {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y)\,dx=\int_{a}^{b}f(x(t),y(t))x' (t)\,dt }}} \tag{3} \end{equation*} \]
and the line integral of \(f\) along \(C\) with respect to \(y\) is given by \[ \begin{equation*} {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y)\,dy=\int_{a}^{b}f(x(t),y(t))y' (t)\,dt }}} \tag{4} \end{equation*} \]
In general, each of these line integrals has a different value.
982
Finding a Line Integral Along \(C\) with Respect to \(x\) and with Respect to \(y\)
Find \[ \int_{C}(x-3y)\,dx\qquad\hbox{and}\qquad \int_{C}(x-3y)\,dy \]
if \(C\) is the part of the parabola \(x=y^{2}\) that joins the points \((1,1)\) and \((4,2)\).
Solution The function \(f(x,y) =x-3y\) is continuous, and \(C\) is a smooth curve everywhere in the plane. So, we can use the formulas (3) and (4). Using the parametric equations of the curve \(C,\) \(x=t^{2}\) and \(y=t\), \(\ 1\leq t\leq 2\), we find \(dx=2t\,dt\) and \(dy=dt\). Then \[ \begin{eqnarray*} \int_{C}(x-3y)\,dx &=&\int_{1}^{2}(t^{2}-3t)2t\,dt=2\int_{1}^{2}(t^{3}-3t^{2}) dt=-\dfrac{13}{2} \notag \\[4pt] \int_{C}(x-3y)\,dy &=&\int_{1}^{2}(t^{2}-3t)\,dt=-\dfrac{13}{6} \end{eqnarray*} \]
NOW WORK
Problem 25.
It is not always necessary to use parametric equations for \(C\) when finding the value of the line integral of a function \(f\). For example, if a smooth curve \(C\) is given by the rectangular equation \(y=g(x)\), \(a\leq x\leq b\), then parametric equations of \(C\) are \[\begin{equation*} x=t\quad y=g(t)\qquad a\leq t\leq b \end{equation*}\]
Since \(dx=dt\) and \(dy=g' (t)\,dt\), we have \[\begin{eqnarray*} \int_{C}f(x,y)\,dx& =&\int_{a}^{b}f(t,g(t))\,dt=\int_{a}^{b}f(x,g(x))\,dx \\[4pt] \int_{C}f(x,y)\,dy& =&\int_{a}^{b}f(t,g(t))g' (t)\,dt=\int_{a}^{b}f(x,g(x))g' (x)\,dx \end{eqnarray*}\]
For example, consider the curve \(C\) in Example 5. \(C\) has the rectangular equation \(y=\sqrt{x}\), \(1\leq x\leq 4\). Then \[ \begin{eqnarray*} \int_{C}(x-3y)\,dx &\underset{ \underset{\color{#0066A7} {\hbox{\(y=\sqrt{x}\)}}} {\color{#0066A7}{\uparrow }}}{=}&\int_{1}^{4}(x-3\sqrt{x})\,dx=-\dfrac{13}{2}\\ \int_{C}(x-3y)\,dy &\underset{ \underset{ \underset{\color{#0066A7} {\hbox{\(dy=\dfrac{1}{2\sqrt{x}}\,dx\)}}} {\color{#0066A7}{\hbox{\(y=\sqrt{x}\)}}}} {\color{#0066A7}{\uparrow }}} {=}&\int_{1}^{4}(x-3\sqrt{x})\left( \dfrac{1}{2\sqrt{x}}\right) dx=-\dfrac{13}{6} \end{eqnarray*} \]
In many applications, we combine the two line integrals \(\int_{C}P(x,y)\, dx\) and \(\int_{C}Q(x,y)\, dy\) using the notation \(\int_{C}(P\,dx+Q\,dy) \).
spanDEFINITIONspan Line Integral \(\int_{C} (P\,dx+Q\,dy) \) Along a Smooth Curve \(C\)
Let \(C\) denote a smooth curve, and let \(P=P(x,y)\) and \(Q=Q(x,y)\) be functions of two variables that are continuous on some region containing \(C\) . The line integral of \(P\,dx+Q\,dy\) along \(C\) is defined as \[ {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}(P\,dx+Q\,dy)=\int_{C}P(x,y)\,dx+\int_{C}Q(x,y)\,dy }}} \]
983
Finding a Line Integral of the Form \(\int_{C}( P\,dx+Q\,dy)\)
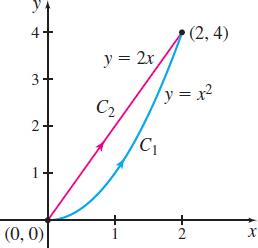
Find the line integral \(\int_{C}(y^{2}\,dx-x^{2}\,dy)\) along
\(C_{1}\): The parabola \(y=x^{2}\) joining the two points \((0,0)\) and \((2,4)\)
\(C_{2}\): The line \(y=2x\) joining the two points \((0,0)\) and \((2,4)\)
Solution The curves \(C_{1}\) and \(C_{2}\) are smooth, and the functions \(P(x,y) =y^{2}\) and \(Q(x,y) = -x^{2}\) are continuous in the \(xy\)-plane.
Along \(C_{1},\) parametric equations for the parabola are \(x(t) =t,\) \(y(t) =t^{2}.\) Then \(dx=dt\) and \(dy=2t\,dt,\) so \[ \begin{eqnarray*} \int_{C_{1}}(y^{2}\,dx-x^{2}\,dy)&=&\int_{C_{1}}y^{2}\,dx-\int_{C_{1}}x^{2}\,dy=\int_{0}^{2}(t^2) ^{2}\,dt-\int_{0}^{2}t^{2}(2t\,dt)\\ &=& \int_{0}^{2}t^{4}\,dt-2\int_{0}^{2}t^{3}\,dt=\left[ \dfrac{t^{5}}{5}\right] _{0}^{2}-\left[ \dfrac{t^{4}}{2}\right] _{0}^{2}=-\dfrac{8}{5} \end{eqnarray*} \]
Along \(C_{2}\), parametric equations for the line segment are \(x(t) =t\), \(y(t) =2t.\) Then \(dx=dt\) and \(dy=2\,dt,\) so \[ \begin{eqnarray*} \int_{C_{2}}(y^{2}\,dx-x^{2}\,dy)&=&\int_{C_{2}}y^{2}\,dx-\int_{C_{2}}x^{2}\,dy=\int_{0}^{2}(2t) ^{2}\,dt-\int_{0}^{2}t^{2}(2\,dt)\\[4pt] &=& \left[ \dfrac{4t^{3}}{3}\right] _{0}^{2}-\left[ \dfrac{2t^{3}}{3}\right] _{0}^{2}=\dfrac{16}{3} \end{eqnarray*} \]
Figure 18 shows the curves \(C_{1}\) and \(C_{2}\) joining the points \(( 0,0) \) and \((2,4) .\)
NOW WORK
Problem 29.
Observe that the value of the line integral in Example 6 depends on the curve \(C\) over which the integration takes place. In the next section, we investigate conditions under which the value of the integral is independent of the curve taken, that is, conditions under which the value of the integral depends only on the endpoints of the curve.
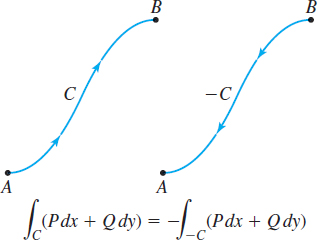
The orientation of the curve \(C\) also plays a role in the value of a line integral over \(C\). If \(C\) is a smooth curve, then \(-C\) is the same curve but with the reverse orientation. Then \[ {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}(P\,dx+Q\,dy)=-\int_{-C}(P\,dx+Q\,dy) }}} \]
That is, reversing the orientation of the curve \(C\) alters the value of the line integral by a factor of \(-1.\) See Figure 19.
The line integral \(\int_{C}(P\,dx+Q\,dy)\) can be written compactly using vectors. Suppose \[ \mathbf{F}=\mathbf{F}(x,y)=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j} \]
NEED TO REVIEW?
The dot product is discussed in Section 10.4, pp. 715-716.
is a vector field that is continuous on some region containing the smooth curve \(C\) traced out by \(\mathbf{r}=\mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}\), \(a\leq t\leq b\). Then \(d\mathbf{r}=dx\mathbf{i}+dy\mathbf{j}\) and the dot product \(\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}\) is \[\begin{equation*} \mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=\left[ P(x,y)\mathbf{i}+Q(x,y)\mathbf{j}\right] \,{\boldsymbol\cdot}\, \left[ dx\mathbf{i}+dy\mathbf{j}\right] =P(x,y) \,dx+Q(x,y) \,dy \end{equation*}\]
So, \[ {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=\int_{C}(P\,dx+Q\,dy) }}} \]
984
Finding a Line Integral of the Form \(\int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}\)
Find \[ \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r} \]
if \(\mathbf{F}(x,y)=x\mathbf{i}+xy\mathbf{j}\) and the curve \(C\) is traced out by the vector function \(\mathbf{r}(t)=t\,\mathbf{i}\,+\,t^{2} \mathbf{j}\), \(0\leq t\leq 2\).
Solution Parametric equations of the curve \(C\) are \[ x(t) =t\qquad y(t) =t^{2}\qquad 0\leq t\leq 2 \]
So, \[ \mathbf{F}=x\mathbf{i}+xy\,\mathbf{j}=t\mathbf{i}+(t) (t^{2}) \mathbf{j}=t\mathbf{i}+t^{3}\mathbf{j} \]
and \[ d\mathbf{r}=\dfrac{d\mathbf{r}}{dt}\,dt=\dfrac{d}{dt}( t\,\mathbf{i} +t^{2}\mathbf{j})\, dt=(\mathbf{i}+2t\mathbf{j})\,dt \]
Then \[ \mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=( t\mathbf{i}+t^{3}\,\mathbf{j}) \,{\boldsymbol\cdot}\, ( \mathbf{i}+2t\,\mathbf{j}) \,dt=( t+2t^{4}) \,dt \]
so that \[ \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=\int_{0}^{2}(t+2t^{4}) \,dt=\dfrac{74}{5} \]
NOW WORK
Problem 47.
4 Find Line Integrals Along a Piecewise-Smooth Curve
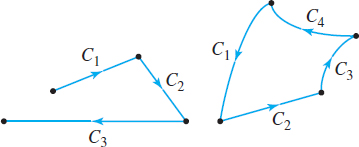
The definition of a line integral of \(f\) along \(C\) assumes that \(C\) is a smooth curve. That is, the parametric equations \(x(t)\) and \(y(t)\) defining \(C\) have derivatives \(\dfrac{dx}{dt}\) and \(\dfrac{dy}{dt}\) that are continuous and are never simultaneously \(0\) on \(a\leq t\leq b\). If a curve \(C \) is not smooth, but consists of a finite number of smooth curves, say, \(C_{1},\,C_{2},\ldots ,C_{n},\) \(n\geq 2\), that are joined together end to end, then \(C\) is a piecewise-smooth curve. Figure 20 shows two piecewise-smooth curves.
spanDEFINITIONspan Line Integral \(\int_{C} (P\,dx+Q\,dy) \) Along a Piecewise-Smooth Curve \(C\)
Let \(C\) be a piecewise-smooth curve consisting of \(n\geq 2\) smooth curves \(C_{1},\) \(C_{2}, \ldots , C_{n}.\) Let \(P=P(x,y)\) and \(Q=Q(x,y)\) be functions of two variables that are each continuous on some region containing \(C\). The line integral \(\int_{C}( P\,dx+Q\,dy)\) along \(C\) is defined as \[ {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}(P\,dx+Q\,dy)=\int_{C_{1}}(P\,dx+Q\,dy)+\int_{C_{2}}(P\,dx+Q\,dy)+ \cdots +\int_{C_{n}}(P\,dx+Q\,dy) }}} \]
If \(\mathbf{F}=P\mathbf{i}+Q\mathbf{j}\) and \(C\) is traced out by \(\mathbf{r} =\mathbf{r}(t) =x(t) \mathbf{i}+y(t) \mathbf{j}\), \(a\leq t\leq b,\) then \[ {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C_{1}}\mathbf{F}\,{\cdot}\, d\mathbf{r}+\int_{C_{2}}\mathbf{F}\,{\cdot}\, d\mathbf{r}+ \cdots +\int_{C_{n}}\mathbf{F} \,{\cdot}\, d\mathbf{r} }}} \]
985
Finding a Line Integral Along a Piecewise-Smooth Curve
Find \(\int_{C}(xy\,dx+x^{2}\,dy)\) along the piecewise-smooth curve \(C\) illustrated in Figure 21.

Solution The values of the line integral along each of the smooth curves \(C_{1},\) \(C_{2},\) \(C_{3}\), and \(C_{4}\) are \[ \begin{eqnarray*} C_{1}{:}&& y =\dfrac{1}{3}x,\quad dy=\dfrac{1}{3}dx;\qquad 0\leq x\leq 3 \\ &&{\int_{C_{1}}(xy\,dx+x^{2}\,dy)=\int_{0}^{3}\left[ x\left( \dfrac{1}{3}x\right) dx+x^{2}\dfrac{1}{3}dx\right] =6} \\ C_{2}{:}&& x =3,\quad dx=0;\qquad 1\leq y\leq 2 \\ &&{\int_{C_{2}}(xy\,dx+x^{2}\,dy)=\int_{1}^{2}9\,dy=9} \\ C_{3}{:}&& y =2, \quad dy=0;\qquad \color{#0066A7}{\hbox{Watch the orientation here: \(x\) varies from 3 to 2.}} \\ &&{\int_{C_{3}}(xy\,dx+x^{2}\,dy)=\int_{3}^{2}2x\,dx=\left[x^{2}\right]^{2}_{3}=-5} \\ C_{4}{:}&& y =x, \quad dy=dx;\qquad \color{#0066A7}{\hbox{Watch the orientation here: \(x\) varies from 2 to 0.}} \\ &&{\int_{C_{4}}(xy\,dx+x^{2}\,dy)=\int_{2}^{0}(x^{2}\,dx+x^{2}\,dx)=2\int_{2}^{0}x^{2}dx=-\dfrac{16}{3}} \end{eqnarray*} \]
Then \[ \int_{C}(xy\,dx+x^{2}\,dy)=6+9-5-\dfrac{16}{3}=\dfrac{14}{3} \]
NOW WORK
Problem 39.
5 Find the Value of a Line Integral in Space
The definition of a line integral in space is similar to that of a line integral in the plane. We state without proof the main results needed to find the value of line integrals in space.
THEOREM The Value of a Line Integral in Space
Let \(C\) be a smooth curve in space defined by the parametric equations \[ x=x(t)\quad y=y(t)\quad z=z(t)\quad a\leq t\leq b \]
Let \(w=f(x,y,z)\) be a function that is continuous on some solid that contains the smooth curve \(C\). Then the line integral of \(f\) along \(C\) from \(t=a\) to \(t=b\) exists and \[ \begin{equation*} {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y,z)\,ds=\int_{a}^{b}f(x(t),y(t),z(t) )\sqrt{\left( \dfrac{dx}{dt}\right) ^{\!\!2}+\left( \dfrac{dy}{dt} \right) ^{\!\!2}+\left( \dfrac{dz}{dt}\right) ^{\!\!2}}dt }}} \tag{5} \end{equation*} \]
Observe that if \(w=f( x,y,z) =1,\) then \[ {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y,z)\,ds=\int_{C}\,ds= \hbox{ arc length of \(C\) from \(a\) to \(b\)} }}} \]
similar to plane curves.
Suppose \(C\) is a smooth curve in space defined by the parametric equations \[\begin{equation*} x=x(t)\quad y=y(t)\quad z=z(t)\qquad a\leq t\leq b \end{equation*}\]
In space, we have line integrals along \(C\) with respect to \(x,\) with respect to \(y,\) and with respect to \(z.\) If \(P(x,y,z),\) \(Q(x,y,z),\) and \(R(x,y,z)\) are functions that are continuous
986
on some solid in space containing \(C\), then \[\begin{eqnarray*} \int_{C}P(x,y,z)\,dx& =&\int_{a}^{b}P(x(t),y(t),z(t))\,x' (t)\,dt \\[4pt] \int_{C}Q(x,y,z)\,dy& =&\int_{a}^{b}Q(x(t),y(t),z(t))\,y' (t)\,dt \\[4pt] \int_{C}R(x,y,z)\,dz& =&\int_{a}^{b}R(x(t),y(t),z(t))\,z' (t)\,dt \\[4pt] \int_{C}(P\,dx+Q\,dy+R\,dz)& =&\int_{C}P\,dx+\int_{C}Q\,dy+\int_{C}R\,dz \end{eqnarray*}\]
If \(\mathbf{F}=\mathbf{F}(x,y,z)=P(x,y,z)\mathbf{i}+Q(x,y,z)\mathbf{j}+R(x,y,z)\mathbf{k}\) is a vector field that is continuous on some solid containing the smooth curve \(C\): \(\mathbf{r}=\mathbf{r}(t)=x(t)\,\mathbf{i}+y(t)\,\mathbf{j}+z(t)\,\mathbf{k}\), \(\ a\leq t\leq b\), then the line integral of \(\mathbf{F \,{\boldsymbol\cdot}\, r}\) is \[ {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}(P\,dx+Q\,dy+R \,dz) }}} \]
A curve \(C\) in space is piecewise-smooth if it consists of a finite number of smooth curves \(C_{1},C_{2},\ldots ,C_{n}\), \(n\geq 2,\) that are joined together end to end. If \(C\): \(\mathbf{r}=\mathbf{r}(t)\) is piecewise-smooth and if \(\mathbf{F}=\mathbf{F}(x,y,z)\) is a vector field that is continuous on some solid containing \(C\), then \[ {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=\int_{C_{1}}\mathbf{F}\,{\boldsymbol\cdot}\, d \mathbf{r}+\int_{C_{2}}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}+\cdots +\int_{C_{n}} \mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r} }}} \]
Finding a Line Integral in Space
Find \(\int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}\) if \[ \begin{equation*} \mathbf{F}(x,y,z)=xy^{2}\,\mathbf{i}+x^{2}z\,\mathbf{j}-(y-x)\,\mathbf{k} \end{equation*} \]
and the curve \(C\) is traced out by \(\mathbf{r}(t)=t\,\mathbf{i}+t^{2}\mathbf{j}+t^{3}\,\mathbf{k}\), \(\ 0\leq t\leq 1\).
Solution Parametric equations of the curve \(C\) are \[ \begin{equation*} x=t\qquad y=t^{2}\qquad z=t^{3}\qquad 0 \le t \le 1 \end{equation*} \]
So, \[ \mathbf{F}=xy^{2}\,\mathbf{i}+x^{2}z\,\mathbf{j}-(y-x)\,\mathbf{k}=t^{5} \mathbf{i}+t^{5}\mathbf{j}-(t^{2}-t)\,\mathbf{k} \]
and \[ d\mathbf{r}=\dfrac{d\mathbf{r}}{dt}\,dt=(\mathbf{i}+2t\mathbf{j}+3t^{2} \mathbf{k})\,dt \]
Then \[ \begin{eqnarray*} \mathbf{F}\,{\cdot}\, d\mathbf{r}&=&[ t^{5}\mathbf{i}+t^{5}\,\mathbf{j} -(t^{2}-t)\,\mathbf{k}] \,{\cdot}\, ( \mathbf{i}+2t\,\mathbf{j}+3t^{2}\, \mathbf{k}) \,dt=[ t^{5}+2t^{6}-3t^{2}(t^{2}-t)] \,dt\\ &=&( 2t^{6}+t^{5}-3t^{4}+3t^{3}) \,dt \end{eqnarray*} \]
so that \[ \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=\int_{0}^{1}(2t^{6}+t^{5}-3t^{4}+3t^{3}) \,dt=\dfrac{253}{420} \]
NOW WORK
Problem 51.
Sections 15.3–15.5 primarily treat line integrals in the plane. We continue the study of line integrals in space in Section 15.9.