Question

True or False A line integral \(\int_{C}f(x,y)\,ds\) is equal to a definite integral if \(C\) is a smooth curve defined on \([a,b]\), and if the function \(f\) is continuous on some region that contains the curve \(C.\)

Question

If \(C\) is a smooth curve defined by the parametric equations \(x=x(t)\) and \(y=y(t),\) \(a\leq t\leq b,\) and \(f\) is a function that is continuous on some region that contains the curve \(C\), then the line integral of \(f\) along \(C\) from \(t=a\) to \(t=b\) exists and is given by \(\int_{C}f(x,y)\,ds=\int_{a}^{b}\)__________\(dt\).

Question

True or False The value \(\int_{C}f(x,y)\,ds\) depends on the choice of the parametric equations used to represent the smooth curve \(C.\)

Question

If the variable mass density of a wire at a point \((x,y) \) is \(\rho (x,y) \), then the mass \(M\) of the wire can be found using the line integral _______, where \(C\) is the curve representing the shape of the wire.

Question

True or False \(\int_{-C}(P\,dx+Q\,dy)= \int_{C}(P\,dx-Q\,dy)\)

Question

True or False A piecewise-smooth curve \(C\) consists of a finite number of smooth curves that are joined together end to end.

Question

If a piecewise-smooth curve \(C\) consists of smooth curves \(C_{1},\,C_{2},\,\ldots ,\,C_{n},\) \(n\geq 2,\) then \(\int_{C}(P\,dx+Q\,dy)=\)_________.

Question

True or False Suppose \(C\) is a smooth curve defined by the parametric equations \(x=x(t),\) \(y=y(t),\) and \(z=z(t),\) \(\ a\leq t\leq b\), and \(P(x,y,z),\) \(Q(x,y,z),\) and \(R(x,y,z)\) are functions that are continuous on some solid in space containing \(C\), then \(\int_{C}P(x,y,z)\,dx=\int_{a}^{b}P( x(t) ,y(t) ,z(t) ) x(t) \,dt.\)

Question

\(\int_{C}x^{2}y\,ds;\quad C\): \(x=\cos t\), \(y=\cos t\) , \(0\leq t\leq \dfrac{\pi }{2}\)

Question

\(\int_{C}(y-x^{2})\, ds;\quad C\): \(x=t\), \(y=3t\), \(0\leq t\leq 1\)

Question

\(\int_{C}xy\,ds;\quad C\): \(x=t^{2},\) \(y=4t,\) \(0\leq t\leq 2\)

Question

\(\int_{C}x\,ds;\quad C\): \(x=t\), \(y=3t^{2}\), \(0\leq t\leq 1\)

Question

\(\int_{C}\dfrac{y}{2x^{2}-y^{2}}ds;\quad C\): \(x=t\), \(y=t\), \(1\leq t\leq 5\)

Question

\(\int_{C}\dfrac{x^{2}}{x^{3}+y^{3}}ds;\quad C\): \(x=3t\), \(y=4t\), \(1\leq t\leq 2\)

Question

Find \(\int_{C}2y\,ds\), where \(C\) is the curve \(y=\dfrac{1}{2}x^{3}\) joining \((0,0)\) to \((2,4)\).

Question

Find \(\int_{C}x\,ds\), where \(C\) is the curve \(x=5y^{3}\) joining \((0,0)\) to \((5,1)\).

Question

Find \(\int_{C}( xy+1) \,ds\), where \(C\) is the curve \(\mathbf{r}(t)=\sin t\mathbf{i}+\cos t\mathbf{j},\) \(0\leq t\leq \pi \).

Question

Find \(\int_{C}xy^{2}\,ds\), where \(C\) is the curve \(\mathbf{r}(t)=\cos t \mathbf{i}+\sin t\mathbf{j},\) \(0\leq t\leq \dfrac{\pi }{2}\).

Question

\(\int_{C}(x+y^{2})\,ds\)

1. \(C_{1}\): \(\ x=t\), \(y=t\), \(0\leq t\leq 1\)
2. \(C_{2}:\) \(\ x=\sin t\), \(y=\sin t\), \(0\leq t\leq \dfrac{\pi }{2}\)

Question

\(\int_{C}(x+y)\,ds\)

1. \(C_{1}\): \(\ x=t\), \(y=3t\), \(0\leq t\leq 1\)
2. \(C_{2}\): \(\ x=\sin (2t) \), \(y=3\sin (2t) ,\) \(0\leq t\leq \dfrac{\pi }{2}\)

Question

\(\int_{C}( x+e^{y}) \,ds\)

1. \(C_{1}\): \(\ x=1-t\), \(y=t\), \(0\leq t\leq 1\)
2. \(C_{2}\): \(\ x=\cos t\), \(y=1-\cos t\), \(0\leq t\leq \dfrac{\pi }{2}\)

Question

\(\int_{C}xe^{x^{2}}ds\)

1. \(C_{1}\): \(\ x=t+1\), \(y=t\), \(0\leq t\leq 1\)
2. \(C_{2}\): \(\ x=1+\sin t\), \(y=\sin t\), \(0\leq t\leq \dfrac{\pi }{2}\)

Question

\(f(x,y) =2x+y^{2}\) along the line \(y=3-x\) from \(\left( 0,3\right) \) to \((3,0) .\)

Question

\(f(x,y) =xe^{y}\) along the line \(2x-y=1\) from \((0,-1) \) to \((1,1) .\)

Question

\(f(x,y) =xe^{y}\) along the curve \(C\) traced out by \(x=e^{2y}\) from \(( 1,0) \) to \((e^{2},1) .\)

Question

\(f(x,y) =x^{2} y\) along the parabola \( x=2y^{2}\) from \((0,0) \) to \(( 2\pi ,\sqrt{\pi }) .\)

Question

Find \(\int_{C}(x^{2}y\,dx+xy\,dy)\) along the curve \(C\): \(x^{2}+y^{2}=1\) from \((1,0)\) to \((0,1)\) using the following parametric equations:

1. \(x=\cos t\), \(y=\sin t\), \(0\leq t\leq \dfrac{\pi }{2}\)
2. \(x=\sqrt{1-y^{2}}\), \(0\leq y\leq 1\)

Question

Find \(\int_{C}(xy\,dx+xy^{2}\,dy)\) along the curve \(C\): \(x^{2}+y^{2}=9\) from \((3,0)\) to \((-3,0)\) traced out by the parametric equations:

1. \(x=3\cos t\), \(y=3\sin t\), \(0\leq t\leq \pi \)
2. \(y=\sqrt{9-x^{2}}\), \(-3\leq x\leq 3\)

Question

Find \(\int_{C}[y^{2}\,dx+(xy-x^{2})\,dy]\) along each of the given curves from \((0,0)\) to \((1,3)\):

1. \(C\) is the line \(y=3x\).
2. \(C\) is the parabola \(y^{2}=9x\).

Question

Find \(\int_{C}[(x^{2}+y^{2})\,dx+3x^{2}y\,dy]\) along each of the given curves from \((-2,4)\) to \((2,4)\):

1. \(C\) is the parabola \(y=x^{2}\).
2. \(C\) is the line \(y=4\).

Question

\(C\) is the curve \(y=x^{2}\) from \((0,0)\) to \((1,1)\).

Question

\(C\) is the curve \(y=x^{3}\) from \((0,0)\) to \((1,1)\).

Question

\(C\) is the curve \(x=\cos t\), \(y=\sin t\), \(0\leq t\leq \dfrac{\pi }{2}\).

Question

\(C\) is the curve \(x=1-t\), \(y=t\), \(0\leq t\leq 1\).

Question

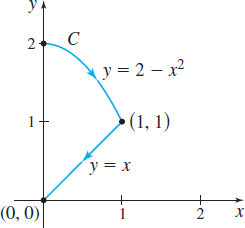
Question

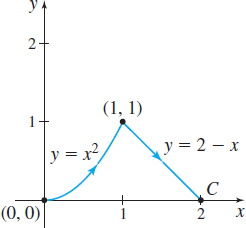
Question

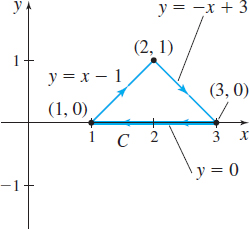
Question

Question

Find \(\int_{C}[(x\cos y)\,dx-(y\sin x)\,dy]\), where \(C\) consists of line segments connecting the points \((0,0)\), \((1,0)\), \((1,1)\) , and \((0,1)\), in that order.

Question

Find \(\int_{C}[(x\sin y)\,dx-(y\cos x)\,dy]\), where \(C\) consists of line segments connecting the points \((0,0)\), \((0,1)\), \((1,1)\), and \((1,0)\), in that order.

Question

Find \(\int_{C}(yz\,dx+xz\,dy+xy\,dz)\), where \(C\) consists of line segments connecting the points \((0,0,0)\), \((1,0,0)\), \((1,1,0)\), and \((1,1,1)\), in that order.

Question

Find \(\int_{C}[yz\,dx+(y+zx)\,dy+xz\,dz]\), where \(C\) consists of line segments connecting the points \((0,0,0)\), \((1,0,0)\), \((1,2,0)\), and \((1,2,1)\), in that order.

Question

The line segment joining the two points

Question

The parabola \(y=4-x^{2}\)

Question

The line segment from \((2,0)\) to \((2,2)\), followed by the line segment from \((2,2)\) to \((0,4)\).

Question

The parabola \(y=4-x^{2}\) from \(( 2,0) \) to \(( 1,3) ,\) followed by the line segment from \(( 1,3) \) to \(( 0,4) \).

Question

\(\mathbf{F}(x,y)=(x+2y)\mathbf{i}+(2x+y)\mathbf{j}\);
\(C\) is the curve \(\mathbf{r}(t)=t\mathbf{i}+t^{2}\mathbf{j}\), \(0\leq t\leq 1\).

Question

\(\mathbf{F}(x,y)=x^{2}\mathbf{i}+xy\mathbf{j}\)
\(C\) is the curve \(\mathbf{r}(t)=(\cos t)\mathbf{i}+(\sin t)\mathbf{j}\), \(0\leq t\leq \pi \).

Question

\(\mathbf{F}(x,y,z)=xy\mathbf{i}+x^{2}z\mathbf{j}+xyz\mathbf{k}\)
\(C\) is the curve \(\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j}+t^{2} \mathbf{k}\), \(0\leq t\leq 1\).

Question

\(\mathbf{F}(x,y,z)=y\mathbf{i}+x^{2}y\mathbf{j}+xz\mathbf{k}\)
\(C\) is the curve \(\mathbf{r}(t)=e^{2t}\mathbf{i}+e^{t}\mathbf{j}+t\mathbf{k}\), \(0\leq t\leq 1\).

Question

\(C\) is the line segment from \((0,0,0)\) to \((1,0,0)\).

Question

\(C\) is the line segment from \((1,0,0)\) to \((1,2,0)\).

Question

\(C\) is the line segment from \((1,2,0)\) to \((1,2,3)\).

Question

\(C\) is the line segment from \((0,0,0)\) to \((1,2,3)\).

Question

\(z=f(x,y)=1-x^{2};\quad C\): \(x=\sin t\), \(y=\cos t\), \(0\leq t\leq 2\pi \)

Question

\(z=f(x,y)=1-y^{2};\quad C\): \(x=\sin t\), \(y=\cos t\), \(0\leq t\leq 2\pi \)

Question

\(z=f(x,y)=2xy;\quad C\): \(y=\sqrt{1-x^{2}}\), \(0\leq x\leq 1\)

Question

\(z=f(x,y)=x+y;\quad C\): \(y=\sqrt{1-x^{2}}\), \(0\leq x\leq 1\)

Question

Find \(\int_{C}\dfrac{\,ds}{x^{2}+y^{2}+z^{2}}\), where \(C\) is the helix \(x=a\cos t\), \(y=a\sin t\), \(z=bt\), \(0\leq t\leq 1\).

Question

Find \(\int_{C}(y^{n}\,dx+x^{n}\,dy)\), where \(C\) is the ellipse \(x=a\sin t\), \(y=b\cos t\), \(0\leq t\leq 2\pi \), and \(n \ge 1\) is an integer.

Question

Find \(\int_{C}y^{2}\,ds\), where \(C\) is the first arch of the cycloid \(x=a(t-\sin t)\), \(y=a(1-\cos t)\).

Question

Find \(\int_{C}\sqrt{x^{2}+y^{2}}\,ds\), where \(C\) is the curve \(x=a(\cos t+t\sin t)\), \(y=a(\sin t-t\cos t)\), \(0\leq t\leq 2\pi \), \(a > 0\).

Question

Find \(\int_{C}(z\,dx+x\,dy+y\,dz)\), where \(C\) is the circular helix \(x=a\cos t\), \(y=a\sin t\), \(z=t\), \(0\leq t\leq 2\pi \).

Question

Find \(\int_{C}[xz\,dx+(y+z)\,dy+x\,dz]\), where \(C\) is the curve \(x=e^{t}\), \(y=e^{-t}\), \(z=e^{2t}\) from \(t=0\) to \(t=1\).

Question

\(C\): \(y=x^{2}\), \(1\leq x\leq 2;\quad \rho =\rho (x,y)=4x\)

Question

\(C\): \(x=3\sin t\), \(y=3\cos t\), \(0\leq t\leq \dfrac{\pi }{2};\quad \rho =\rho (x,y)=x+y+1\)

Question

Mass of a Wire Find the mass of a thin wire in the shape of a parabola \(x=2t^{2},\) \(y=t\), \(-2\leq t\leq 3\), if the variable mass density of the wire is \(\rho (x,y) =3x.\)

Question

Mass of a Wire Find the mass of a thin wire in the shape of a parabola \(x=t,\) \(y=t^{2}-1,\) \(0\leq t\leq 3,\) if the variable mass density of the wire is \(\rho (x,y) =x\left( y+1\right) .\)

Question

Mass of a Wire A spring is made of a thin wire twisted into the shape of a circular helix \(x=2\cos t\), \(y=2\sin t,\) \(z=t.\) Find the mass of two turns of the spring if the wire has constant mass density \(\rho\).

989

Question

Mass of a Wire A spring is made of a thin wire twisted into the shape of a circular helix \(x=3\sin t\), \(y=3\cos t,\) \(z=t.\) Find the mass of two turns of the spring if the wire has variable mass density \(\rho ( x,y,z) =z+2.\)

Question

Mass of a Wire in Space Write a formula similar to \(M=\int_{C}\rho (x,y)\, ds\) for the mass of a thin wire in the shape of a smooth space curve \(C\) whose variable mass density is \(\rho =\rho (x,y,z)\).

Question

Mass of a Wire in Space The thin wire is in the shape of the helix \(C\): \(x=2\cos t\), \(y=2\sin t\), \(z=5t\), \(0\leq t\leq 2\pi \), whose mass density is \(\rho (x,y,z)=k\), a constant.

Question

Mass of a Wire in Space The thin wire is in the shape of a helix \(C\): \(x=3\cos t\), \(y=3\sin t\), \(z=4t\), \(0\leq t\leq 2\pi \), whose variable mass density is \(\rho (x,y,z)=2+z\).

Question

Mass of a Wire in Space The thin wire is in the shape of a helix \(C\): \(x=2\cos t\), \(y=2\sin t\), \(z=5t\), \(0\leq t\leq 2\pi \), if the mass density is proportional to the square of the distance from the origin.

Question

Lateral Surface Area Derive the formula \(A=2\pi Rh\) for the surface area of a right circular cylinder using the line integral \(\int_{C}f(x,y)\,ds\), where \(z=f(x,y)=h\), \(h>0\), and \(C\) is the circle \(x^{2}+y^{2}=R^{2}\).

Question

Let \(C_{1}\) be the curve \(x=\cos \theta \), \(y=\sin \theta \), \(0\leq \theta \leq 4\pi \), and let \(C_{2}\) be the curve \(x=\cos t^{2}\), \(y=\sin t^{2}\), \(0\leq t\leq 2\sqrt{\pi }\). For \(P(x,y) =x^{3}y\) and \(Q(x,y) =y^{2}x\), show that \(\int_{C_{1}}(P\,dx+Q\,dy)=\int_{C_{2}}(P\,dx+Q\,dy)\). Explain why this is so.

Question

Find \(\int_{C}(x+y)\,ds\), where \(C\) is the curve \(x=t\), \(y=\dfrac{3t^{2}}{\sqrt{2}}\), \(0\leq t\leq 1\).

Question

Center of Mass Find the center of mass of a homogeneous wire in the shape of the hypocycloid

1. \( x=a\cos ^{3}t,y=a\sin ^{3}t,\ 0\leq t\leq \dfrac{\pi }{2}\)
2. \( x=a\cos ^{3}t,y=a\sin ^{3}t,\ 0\leq t\leq 2\pi \)

Question

Suppose the line integral of \(f(x,y)\) along the curve \(C\) exists.

1. Use the Mean Value Theorem to derive the formula \[ \int_{C}f(x,y)\,ds=\int_{a}^{b}f(x(t),y(t))\sqrt{\left( \dfrac{dx}{dt} \right) ^{\!\!2}+\left( \dfrac{dy}{dt}\right) ^{\!\!2}}\,dt \]
2. Apply the formula in (a) to the quantity \(S(t)=\int_{a}^{t}\sqrt{(x')^2+(y')^2}\,du\), where \(S' (t_{0})\) is the length of the portion of the curve traced out as \(t\) moves from \(a\) to \(t_{0}\).

Question

It follows from Problem 79 that the value of a line integral of a function along a smooth curve, given the hypotheses of the theorem, is independent of the parameterization. Why? In particular, if \(x\) and \(y\) are differentiable functions of the arc length as one moves along the curve, describe what form the integral \[ \int_{C}f(x,y)\,ds=\int_{a}^{b}f(x(t),y(t)) \sqrt{\left( \dfrac{dx}{dt}\right) ^{\!\!2}+\left( \dfrac{dy}{dt}\right) ^{\!\!2}} \,dt \]

takes when \(s\) is used as the parameter.

Question

We have seen two kinds of line integrals: \(\int_{C}( P\,dx+Q\,dy) \) and \(\int_{C}f\,ds\). These are closely connected.

1. If \(C\) is expressed using arc length as the parameter, show that \(\int_{c}(Pdx + Qdy)\) can be written in the form \(\int_{c} fds\).
2. If the arc length \(s\) along \(C\) can be expressed as a function of \(x\) and \(y\), show that \(\int_{c}fds\) can be written in the form \(\int_{c}(Pdx + Qdy)\). For example, \[ \int_{C}(x+y^{2})\,ds=\int_{C}\left[\dfrac{x^{2}+xy^{2}}{\sqrt{x^{2}+y^{2}}}\,dx+ \dfrac{xy+y^{3}}{\sqrt{x^{2}+y^{2}}}\,dy\right] \] where \(C\) is the curve \(x=t\), \(y=t\), for \(0\leq t\leq 1\).