P.5 Exponential and Logarithmic Functions
38
OBJECTIVES
When you finish this section, you should be able to:
- Analyze an exponential function (p. 38)
- Define the number e (p. 41)
- Analyze a logarithmic function (p. 42)
- Solve exponential equations and logarithmic equations (p. 45)
Here we begin our study of transcendental functions with the exponential and logarithmic functions. In Section P.6 and P.7, we investigate the trigonometric functions and their inverse functions.
1 Analyze an Exponential Function
The expression \(a^{r}\), where \(a>0\) is a fixed real number and \(r=\dfrac{m}{n}\) is a rational number, in lowest terms with \(n\geq 2\), is defined as \[ a^{r}=a^{m/n}=( a^{1/n}) ^{m}=( \sqrt[n]{a}) ^{m} \]
39
So, a function \(f( x) =a^{x}\) can be defined so that its domain is the set of rational numbers. Our aim is to expand the domain of \(f\) to include both rational and irrational numbers, that is, to include all real numbers.
CAUTION
Be careful to distinguish an exponential function \(f ( x) =a^{x}\), where \(a>0\) and \(a\neq 1\), from a power function \(g ( x ) =x^{a}\), where \(a\) is a real number. In \({f} ({x}) =a^{x}\) the independent variable \(x\) is the exponent; in \({g} ( {x}) =x^{a}\) the independent variable \({x}\) is the base.
Every irrational number \(x\) can be approximated by a rational number \(r\) formed by truncating (removing) all but a finite number of digits from \(x\). For example, for \(x=\) \(\pi \), we could use the rational numbers \(r=3.14\) or \(r=3.14159\), and so on. The closer \(r\) is to \(\pi \), the better approximation \(a^{r}\) is to \(a^{\pi }\). In general, we can make \(a^{r}\) as close as we please to \(a^{x}\) by choosing \(r\) sufficiently close to \(x.\) Using this argument, we can define an exponential function \(f( x) =a^{x}\), where \(x\) includes all the rational numbers and all the irrational numbers.
spanDEFINITIONspan Exponential Function
An exponential function is a function that can be expressed in the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ f(x) =a^{x} }} \] where \(a\) is a positive real number and \(a\neq 1\). The domain of \(f\) is the set of all real numbers.
NOTE
The base \(a=1\) is excluded from the definition of an exponential function because \(f(x) =1^{x}=1\) (a constant function). Bases that are negative are excluded because \({a}^{1/n}\), where \(a<0\) and \({n}\) is an even integer, is not defined.
Examples of exponential functions are \(f( x) =2^{x}\), \( g( x) =\left( \dfrac{2}{3}\right)^{\!\!\!x}\), and \(h( x) =\pi ^{x}\).
Consider the exponential function \(f( x) =2^{x}\). The domain of \( f\) is all real numbers; the range of \(f\) is the interval \(\left( 0,\infty \right) .\) Some points on the graph of \(f\) are listed in Table 4. Since \( 2^{x}>0\) for all \(x\), the graph of \(f\) lies above the \(x\)-axis and has no \(x\) -intercept. The \(y\)-intercept is \(1\). Using this information, plot some points from Table 4 and connect them with a smooth curve, as shown in Figure 59.
| \(x\) | \(f( x) = 2^{x}\) | \((x,y)\) |
|---|---|---|
| \(-10\) | \(2^{-10}\approx 0.00098\) | \((-10,0.00098)\) |
| \(-3\) | \(2^{-3}=\dfrac{1}{8}\) | \(\left( -3,\dfrac{1}{8}\!\right)\) |
| \(-2\) | \(2^{-2}=\dfrac{1}{4}\) | \(\left( -2,\dfrac{1}{4}\!\right)\) |
| \(-1\) | \(2^{-1}=\dfrac{1}{2}\) | \(\left( -1,\dfrac{1}{2}\!\right)\) |
| 0 | \(2^{0}=1\) | \((0,1)\) |
| 1 | \(2^{1}=2\) | \((1,2)\) |
| 2 | \(2^{2}=4\) | \((2,4)\) |
| 3 | \(2^{3}=8\) | \((3,8)\) |
| 10 | \(2^{10}=1024\) | ( 10,1024) |
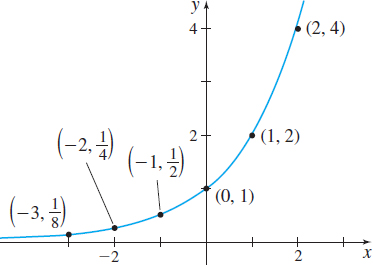
The graph of \(f( x) =2^{x}\) is typical of all exponential functions of the form \(f( x) =a^{x}\) with \(a>1\), a few of which are graphed in Figure 60.
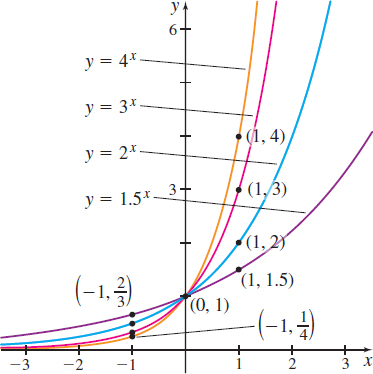
Notice that every graph in Figure 60 lies above the \(x\)-axis, passes through the point \((0,1)\), and is increasing. Also notice that the graphs with larger bases are steeper when \(x>0\), but when \(x<0\), the graphs with larger bases are closer to the \(x\)-axis.
40
All functions of the type \(f( x) =a^{x}\), \(a>1\), have the following properties:
Properties of an Exponential Function \(f( x) =a^{x}, a>1\)
- The domain is the set of all real numbers; the range is the set of positive real numbers.
- There are no \(x\)-intercepts; the \(y\)-intercept is \(1\).
- The exponential function \(f\) is increasing on the interval \(( -\infty ,\infty ) \).
- The graph of \(f\) contains the points \(\left( -1,\dfrac{1}{a}\!\right) \), \(( 0,1) \), and \(( 1,a) .\)
- \(\dfrac{f( x+1) }{f( x) }=a\)
- Because \(f (x) = a^x\) is a function, if \(u = v\), then \(a^u = a^v\).
- Because \(f (x) = a^x\) is a one-to-one function, if \(a^u = a^v\), then \(u = v\).
NEED TO REVIEW?
The laws of exponents are discussed in Appendix A.1,\(\!\!\!\!\!\!\!\!\!\!\) pp. A-8 to A-9.
THEOREM Laws of Exponents
If \(u\), \(v\), \(a\), and \(b\) are real numbers with \(a>0\) and \(b>0\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ a^{u}\cdot a^{v}=a^{u+v} \ \quad \dfrac{a^{u}}{a^{v}}=a^{u-v}\ \quad ( a^{u}) ^{v}=a^{uv} \ \quad (ab) ^{u}=a^{u}\cdot b^{u}\ \quad \left( \dfrac{a}{b}\!\right) ^{\!\!u}=\dfrac{a^{u}}{b^{u}} }} \]
For example, we can use the Laws of Exponents to show the following property of an exponential function: \[ \dfrac{f( x+1) }{f( x) }=\dfrac{a^{x+1}}{a^{x}}=a^{( x+1) -x}=a^{1}=a \]
Graphing an Exponential Function
Graph the exponential function \(g( x) =\left( \dfrac{1}{2}\!\right) ^{\!\!\!x}.\)
Solution We begin by writing \(\dfrac{1}{2}\) as \(2^{-1}\). Then \[ g( x) =\left( \dfrac{1}{2}\!\right) ^{\!\!\!x}=( 2^{-1}) ^{x}=2^{-x} \]
Now we use the graph of \(f( x) =2^{x}\) shown in Figure 59 and reflect it about the \(y\)-axis to obtain the graph \(g( x) =2^{-x}.\) See Figure 61.
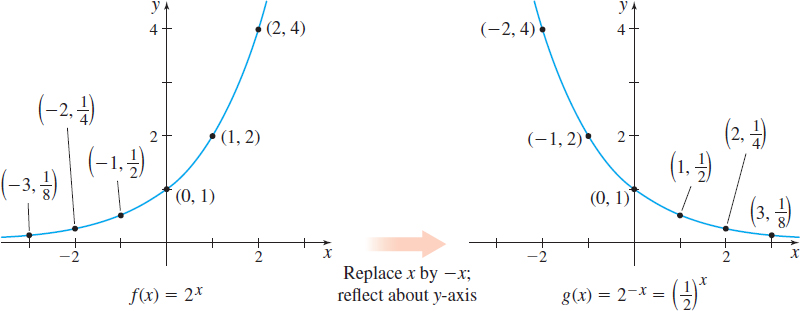
NOW WORK
Problem 19.
41
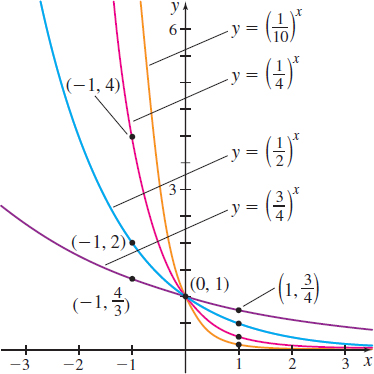
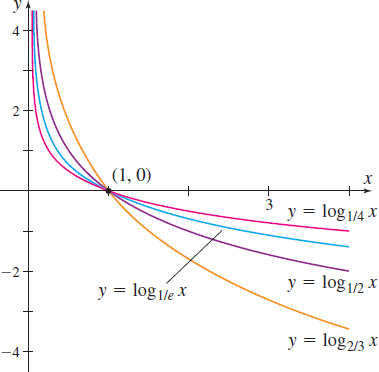
The graph of \(g( x) =\left( \dfrac{1}{2}\!\right) ^{\!\!\!x}\) in Figure 61 is typical of all exponential functions that have a base between 0 and 1. Figure 62 illustrates the graphs of several more exponential functions whose bases are between \(0\) and \(1.\) Notice that the graphs with smaller bases are steeper when \(x<0\), but when \(x>0\), these graphs are closer to the \(x\)-axis.
Properties of an Exponential Function \(f( x)=a^{x}\), \(0<a<1\)
- The domain is the set of all real numbers; the range is the set of positive real numbers.
- There are no \(x\)-intercepts; the \(y\)-intercept is \(1\).
- The exponential function \(f\) is decreasing on the interval \(( -\infty ,\infty ) \).
- The graph of \(f\) contains the points \(\left( -1,\dfrac{1}{a}\!\right)\), \(( 0,1) \), and \(( 1,a)\).
- \(\dfrac{f( x+1) }{f( x) }=a\)
- If \(u=v\), then \(a^{u}=a^{v}\).
- If \(a^{u}=a^{v}\), then \(u=v.\)
Graphing an Exponential Function Using Transformations
Graph \(f( x) =3^{-x}-2\) and determine the domain and range of \(f.\)
Solution We begin with the graph of \(y=3^{x}.\) Figure 63 shows the steps.
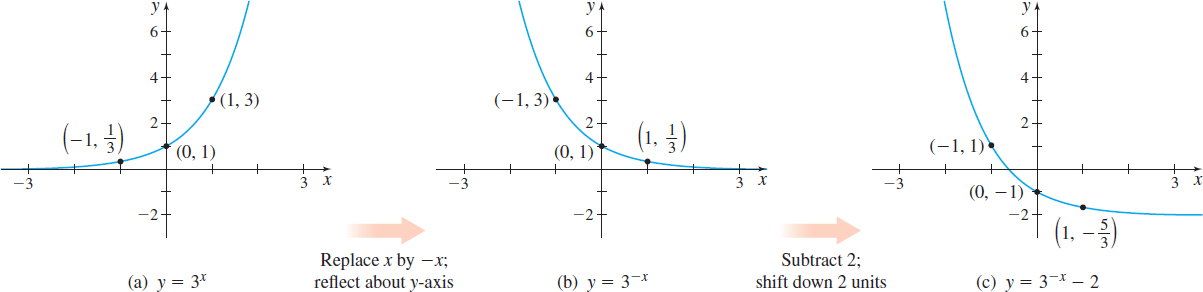
The domain of \(f\) is all real numbers, the range of \(f\) is the interval \((-2,\infty\)).
NOW WORK
Problem 27.
2 Define the Number e
In earlier courses you learned about an irrational number, called \(e\). The number \(e\) is important because it appears in many applications and because it has properties that simplify computations in calculus.
To define \(e\), consider the graphs of the functions \(y=2^{x}\) and \(y=3^{x}\) in Figure 64(a), where we have carefully drawn lines that just touch each graph at the point \(( 0,1)\). (These lines are tangent lines, which we discuss in Chapter 1.) Notice that the slope of the tangent line to \(y=3^{x}\) is greater than \(1\) (approximately \(1.10\)) and that the slope of the tangent line to the graph of \(y=2^{x}\) is less than 1 (approximately \(0.69\)). Between these graphs there is an exponential function \(y=a^{x}\), whose base is between \(2\) and \(3\), and whose tangent line to the graph at the point \(( 0,1)\) has a slope of exactly 1, as shown in Figure 64(b). The base of this exponential function is the number \(e.\)


ORIGINS
The irrational number we call \(e\) was named to honor the Swiss mathematician Leonhard Euler (1707–1783), who is considered one of the greatest mathematicians of all time. Euler was encouraged to study mathematics by his father. Considered the most prolific mathematician who ever lived, he made major contributions to many areas of mathematics. One of Euler's greatest gifts was his ability to explain difficult mathematical concepts in simple language.
spanDEFINITIONspan The number \(e\)
The number \(e\) is defined as the base of the exponential function whose tangent line to the graph at the point \(\left( 0,1\right)\) has slope \(1\). The function \(f( x) =e^{x}\) occurs with such frequency that it is usually referred to as the exponential function.
The number \(e\) is an irrational number, and in Chapter 3, we will show \(e\approx 2.71828\).
3 Analyze a Logarithmic Function
NEED TO REVIEW?
Logarithms and their properties are discussed in Appendix A.1, pp. A-10 to A-11.
Recall that a one-to-one function \(y=f(x)\) has an inverse function that is defined implicitly by the equation \(x=f( y) .\) Since an exponential function \(y=f( x) =a^{x}\), where \(a>0\) and \( a\neq 1\), is a one-to-one function, it has an inverse function, called a logarithmic function, that is defined implicitly by the equation \[ x=a^{y}\qquad \hbox{where }a>0\quad {\rm and} \quad a\neq 1 \]
IN WORDS
A logarithm is an exponent. That is, if \(y=\log _{a}{x}\), then \({y}\) is the exponent in \(x=a^{y}\).
42
spanDEFINITIONspan Logarithmic Function
The logarithmic function with base \(a\), where \(a>0\) and \( a\neq 1\), is denoted by \(y=\log _{a}x\) and is defined by \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ y=\log _{a}x\quad \hbox{if and only if}\quad x=a^{y} }} \]
The domain of the logarithmic function \(y=\log _{a}x\) is \(x>0\).
In other words, if \(f( x) =a^{x}\), where \(a>0\) and \(a\neq 1\), its inverse function is \(f^{-1}( x) =\log _{a}x.\)
If the base of a logarithmic function is the number \(e\), then it is called the natural logarithmic function, and it is given a special symbol, ln (from the Latin, logarithmus naturalis). That is, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ y=\ln x\quad \hbox{if and only if}\quad x=e^{y} }} \]
Since the exponential function \(y=a^{x}\), \(a>0,a\neq 1\) and the logarithmic function \(y=\log _{a}x\) are inverse functions, the following properties hold:
- \(\log _{a}( a^{x}) = x \hbox{ for all real numbers }x\)
- \(a^{\log _{a}x} =x \hbox{ for all }x>0\)
43
Because exponential functions and logarithmic functions are inverses of each other, the graph of the logarithmic function \(y=\log _{a}x\), \(a>0\) and \( a\neq 1\), is the reflection of the graph of the exponential function \(y=a^{x}\), about the line \(y=x\), as shown in Figure 65.
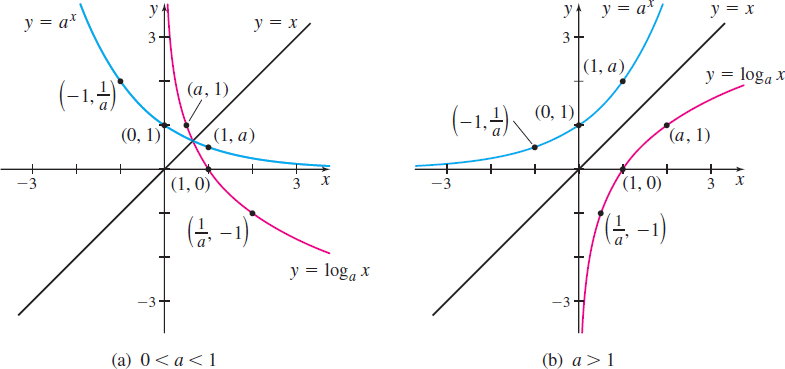
Based on the graphs in Figure 65, we see that \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \log _{a}1=0\qquad \log _{a}a=1\qquad a>0\quad \hbox{and}\quad a\neq 1 }} \]
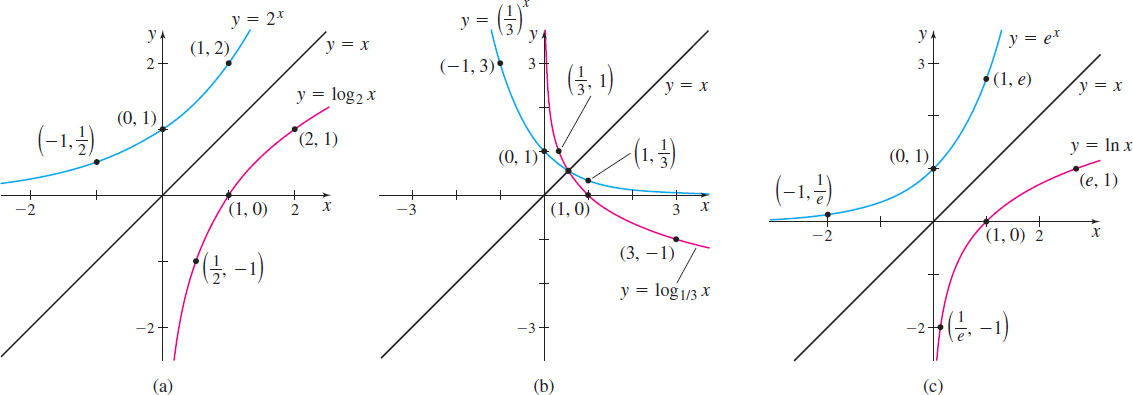
Graphing a Logarithmic Function
Graph:
- \(f( x) =\log _{2}x\)
- \(g( x) =\log _{1/3}x\)
- \(F( x) =\ln x\)
Solution (a) To graph \(f( x) =\log _{2}x\), graph \( y=2^{x}\) and reflect it about the line \(y=x.\) See Figure 66(a).
(b) To graph \(f( x) =\log _{1/3}x\), graph \( y=\left( \dfrac{1}{3}\!\right) ^{\!\!\!x}\) and reflect it about the line \(y=x.\) See Figure 66(b).
(c) To graph \(F( x) =\ln x\), graph \(y=e^{x}\) and reflect it about the line \(y=x\). See Figure 66(c).
NOW WORK
Problem 39.
44
Since a logarithmic function is the inverse of an exponential function, it follows that:
- Domain of the logarithmic function \(=\) Range of the exponential function \(=( 0,\infty ) \)
- Range of the logarithmic function \(=\) Domain of the exponential function \(=( -\infty ,\infty)\)
The domain of a logarithmic function is the set of positive real numbers, so the argument of a logarithmic function must be greater than zero.
Finding the Domain of a Logarithmic Function
Find the domain of each function:
- \(F( x) =\log _{2}( x+3)\)
- \(g( x) =\ln \left( \dfrac{1+x}{1-x}\!\right)\)
- \(h( x) =\log _{1/2}\vert x\vert\)
NEED TO REVIEW?
Solving inequalities is discussed in Appendix A.1,\(\!\!\!\!\!\!\!\!\!\!\!\) pp. A-5 to A-8.
Solution (a) The argument of a logarithm must be positive. So to find the domain of \(F( x) =\log _{2}( x+3) \), we solve the inequality \(x+3>0.\) The domain of \(F\) is \(\{ x | x >-3\} \).
| Interval | Test Number | Sign of \(\dfrac{{1+x}}{{1-x}}\) |
|---|---|---|
| \(( -\infty ,-1) \) | \(-2\) | Negative |
| \(( -1,1) \) | \(0\) | Positive |
| \(( 1,\infty ) \) | \(2\) | Negative |
(b) Since \(\ln \left( \dfrac{1+x}{1-x}\!\right)\) requires \(\dfrac{1+x}{ 1-x}>0\), we find the domain of \(g\) by solving the inequality \(\dfrac{1+x}{1-x} >0.\) Since \(\dfrac{1+x}{1-x}\) is not defined for \(x=1\), and the solution to the equation \(\dfrac{1+x}{1-x}=0\) is \(x=-1\), we use \(-1\) and \(1\) to separate the real number line into three intervals \(( -\infty ,-1) \), \(( -1,1) \), and \(( 1,\infty ) .\) Then we choose a test number in each interval, and evaluate the rational expression \(\dfrac{1+x}{1-x}\) at these numbers to determine if the expression is positive or negative. For example, we chose the numbers \(-2\), \(0\), and \(2\) and found that \(\dfrac{1+x}{ 1-x}>0\) on the interval \(( -1,1)\). See the table on the left. So the domain of \(g( x) =\ln \left( \dfrac{1+x}{1-x}\!\right) \) is \(\{ x|{-}1<x<1\}\).
(c) \(\log _{1/2}\vert x\vert \) requires \( \vert x\vert >0\). So the domain of \(h( x) =\log _{1/2}\vert x\vert \) is \( \{ x|x \neq 0\} .\)
NOW WORK
Problem 31.
Properties of a Logarithmic Function \(f( x) = \log _{a}x\), \(a>0\) and \(a\neq 1\)
- The domain of \(f\) is the set of all positive real numbers; the range is the set of all real numbers.
- The \(x\)-intercept of the graph of \(f\) is \(1\). There is no \(y\) -intercept.
- A logarithmic function is decreasing on the interval \(( 0,\infty ) \) if \(0<a<1\) and increasing on the interval \(( 0,\infty ) \) if \(a>1\).
- The graph of \(f\) contains the points \(( 1,0) \), \(( a,1) \), and \(\left( \dfrac{1}{a},-1\right) .\)
- Because \(f (x) = \log_a x\) is a function, if \(u = v\), then \(\log_a u = \log_a v\).
- Because \(f (x) = \log_a x\) is a one-to-one function, if \(\log_a u = \log_a v\), then \(u = v\).
- See Figure 67 for typical graphs with base \(a\), \(a>1;\) see Figure 68 for graphs with base \(a\), \(0<a<1.\)
45
4 Solve Exponential Equations and Logarithmic Equations
Equations that involve terms of the form \(a^{x}\), \(a>0\), \(a\neq 1\), are referred to as exponential equations. For example, the equation of the form \(5^{2x+3}=5^{x}\) is an exponential equation.
IN WORDS
In an exponential equation, if the bases are equal, then the exponents are equal.
The one-to-one property of exponential functions \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \hbox{if } a^{u}=a^{v}\quad \hbox{then } u=v }}\tag{1} \]
can be used to solve certain kinds of exponential equations.
Solving Exponential Equations
Solve each exponential equation:
- \(4^{2x-1}=8^{x+3}\)
- \(e^{-x^{2}}=( e^{x}) ^{2}\cdot \dfrac{1}{e^{3}}\)
Solution (a) We begin by expressing both sides of the equation with the same base so we can use the one-to-one property (1). \[ \begin{array}{rcl@{\qquad}l} 4^{2x-1}&=&8^{x+3} \\[3pt] (2^{2}) ^{2x-1}&=& ( 2^{3}) ^{x+3} & {\color{#0066A7}{{\hbox{${4=2}^{2}, {8=2}^{3}$}}}} \\[3pt] 2^{2 ( 2x-1) }&=&2^{3( x+3) } & {\color{#0066A7}{{({a}^{r}) ^{s}{=a}^{rs}}}} \\[3pt] 2 ( 2x-1)~&=&3 ( x+3)~& {\color{#0066A7}{{\hbox{If } {a}^{u}=a^{v}, \hbox{then } u=v.}}} \\[3pt] 4x-2 &=& 3x+9 & {\color{#0066A7}{{\hbox{Simplify.}}}} \\[3pt] x &=& 11 & {\color{#0066A7}{{\hbox{Solve.}}}} \end{array} \] The solution is 11.
(b) We use the Laws of Exponents to obtain the base \(e\) on the right side. \[ ( e^{x}) ^{2}\cdot \dfrac{1}{e^{3}}=e^{2x}\cdot e^{-3}=e^{2x-3} \] As a result, \[ \begin{array}{rcl@{\qquad}l} e^{-x^{2}} &=&e^{2x-3} \\[3pt] -x^{2} &=&2x-3 & {\color{#0066A7}{{\hbox{If } {a}^{u}=a^{v}, \hbox{ then } u=v.}}} \\[3pt] x^{2}+2x-3 &=&0 \\[3pt] ( x+3) ( x-1)~&=&0 \\[3pt] x &=&-3\quad \hbox{or}\quad x=1 \end{array} \] The solution set is \(\{ -3,1\}\).
NOW WORK
Problem 49.
46
To use the one-to-one property of exponential functions, each side of the equation must be written with the same base. Since for many exponential equations it is not possible to write each side with the same base, we need a different strategy to solve such equations.
Solving Exponential Equations
Solve the exponential equations:
- \(10^{2x}=50\)
- \(8\cdot 3^{x}=5\)
RECALL
that logarithms to the base \(10\) are called common logarithms and are written without a subscript. That is, \(x=\log _{10}{y}\) is written \(x=\log y\).
Solution (a) Since \(10\) and \(50\) cannot be written with the same base, we write the exponential equation as a logarithm. \[ 10^{2x}=50\quad \hbox{if and only if}\quad \log 50=2x \] Then \(x=\dfrac{\log 50}{2}\) is an exact solution of the equation. Using a calculator, an approximate solution is \(x=\dfrac{\log 50}{2}\approx 0.849\).
(b) It is impossible to write \(8\) and \(5\) as a power of \(3\), so we write the exponential equation as a logarithm. \[ \begin{eqnarray*} 8\cdot 3^{x} &=&5 \\[5pt] 3^{x} &=&\dfrac{5}{8} \\[5pt] \log _{3} \dfrac{5}{8} &=&x \end{eqnarray*} \] Now we use the change-of-base formula to obtain the exact solution of the equation. An approximate solution can then be obtained using a calculator. \[ x=\log _{3} \dfrac{5}{8} =\dfrac{\ln \dfrac{5}{8} }{\ln 3}\approx -0.428 \]
NEED TO REVIEW?
The change-of-base formula, \(\log _{a} u=\dfrac{\log _{b}u}{\log _{b}a}\),\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\) \(a\neq 1\), \(b\neq 1\), and \({u}\) positive real numbers, is discussed in Appendix A.1, p. A-11.
Alternatively, we could have solved each of the equations in Example 6 by taking the natural logarithm (or the common logarithm) of each side. For example, \[ \begin{array}{rcl@{\qquad}l} 8\cdot 3^{x} &=&5 \\[5pt] 3^{x} &=&\dfrac{5}{8} \\[5pt] \ln 3^{x} &=&\ln \dfrac{5}{8} & {\color{#0066A7}{{\hbox{If } u=v, \hbox{ then } \log _{a}u=\log _{a}{v}.}}} \\[5pt] x\ln 3 &=&\ln \dfrac{5}{8} & {\color{#0066A7}{{\log _{a}{u}^{r}{=r}\log _{a}{u}}}} \\[5pt] x &=&\dfrac{\ln \dfrac{5}{8} }{\ln 3} \end{array} \]
NOW WORK
Problem 51.
Equations that contain logarithms are called logarithmic equations. Care must be taken when solving logarithmic equations algebraically. In the expression \(\log _{a} y\), remember that \(a\) and \(y\) are positive and \(a\neq 1\). Be sure to check each apparent solution in the original equation and to discard any solutions that are extraneous.
Some logarithmic equations can be solved by changing the logarithmic equation to an exponential equation using the fact that \(x=\log _{a} y\) if and only if \(y=a^{x}\).
47
Solving Logarithmic Equations
Solve each equation:
- \(\log _{3}( 4x-7) =2\)
- \(\log _{x}64=2\)
Solution (a) We change the logarithmic equation to an exponential equation. \[ \begin{eqnarray*} \log _{3}( 4x-7)~&=&2 \\[3pt] 4x-7 &=&3^{2}{\rm \ \ \ \ \ \ \ \ {\color{#0066A7}{{\hbox{Change to an exponential equation.}}}}} \\[3pt] 4x-7 &=&9 \\[3pt] 4x &=&16 \\[3pt] x &=&4 \end{eqnarray*} \]
Check: For \(x=4\), \(\log _{3}( 4x-7) =\log _{3}( 4\cdot 4-7) =\log _{3}9=2\), since \(3^{2}=9\).
The solution is \(4\).
(b) We change the logarithmic equation to an exponential equation. \[ \begin{array}{rcl@{\quad\qquad}l} \log _{x}64 &=&2 \\[3pt] x^{2} &=&64 & {\color{#0066A7}{{\hbox{Change to an exponential equation.}}}} \\[3pt] x &=& 8 \quad \hbox{or}\quad x=-8 & {\color{#0066A7}{{\hbox{Solve.}}}} \end{array} \]
The base of a logarithm is always positive. As a result, we discard \(-8\) and check the solution \(8\).
Check: For \(x=8\), \(\log _{8} 64=2\), since \(8^{2}=64.\)
The solution is \(8\).
NOW WORK
Problem 57.
The properties of logarithms that result from the fact that a logarithmic function is one-to-one can be used to solve some equations that contain two logarithms with the same base.

Solving a Logarithmic Equation
Solve the logarithmic equation \(2\ln x=\ln 9\).
Solution Each logarithm has the same base, so \[ \begin{array}{rcl@{\quad\qquad}l} 2\ln x &=&\ln 9 \\[4pt] \ln x^{2} &=&\ln 9 & {\hbox{\({\color{#0066A7}{r\log _{a} u=\log _{a}{u}^{r}}}\)}} \\[4pt] x^{2} &=&9 & {\color{#0066A7}{{\hbox{If }\log _{a} u=\log _{a}v, \hbox{ then } u=v.}}} \\[4pt] x &=&3\quad \hbox{or}\quad x=-3 \end{array} \]
We discard the solution \(x=-3\) since \(-3\) is not in the domain of \(f( x) =\ln x\). The solution is 3.
NOW WORK
Problem 61.
Although, each of these equations was relatively easy to solve, this is not generally the case. Many solutions to exponential and logarithmic equations need to be approximated using technology.
48

Approximating the Solution to an Exponential Equation
![]()
Solve \(x+e^{x}=2.\) Express the solution rounded to three decimal places.
Solution We can approximate the solution to the equation by graphing the two functions \(Y_{1}=x+e^{x}\) and \(Y_{2}=2.\) Then we use graphing technology to approximate the intersection of the graphs. Since the function \(Y_{1}\) is increasing (do you know why?) and the function \(Y_{2}\) is constant, there will be only one point of intersection. Figure 69 shows the graphs of the two functions and their intersection. They intersect when \( x\approx 0.4428544\), so the solution of the equation is \(0.443\) rounded to three decimal places.
NOW WORK
Problem 65.