Preparing for Calculus

P.6 Assess Your Understanding
Printed Page 56

Concepts and Vocabulary

The sine, cosine, cosecant, and secant functions have period _____; the tangent and cotangent functions have period _____.

$2\pi$ , $\pi$

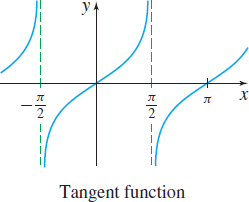
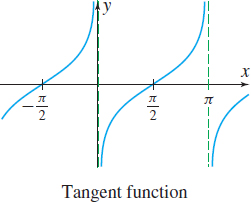
The domain of the tangent function $f( x) = \tan x$ is _____.

All real numbers except odd multiples of $\frac{\pi}{2}$

The range of the sine function $f( x) = \sin x$ is _____.

$\{y | -1 \le y \le 1\}$

Explain why $\tan\! \left(\! \dfrac{\pi }{4}+2\pi \right) =\tan \dfrac{\pi }{4}$ .

The period of $\tan x$ is $\pi$ .

True or False The range of the secant function is the set of all positive real numbers.

False

The function $f( x) = 3\cos (6x)$ has amplitude _____ and period _____.

$3$ , $\frac{\pi}{3}$

True or False The graphs of $y=\sin x$ and $y=\cos x$ are identical except for a horizontal shift.

True

True or False The amplitude of the function $f( x) =2\sin ( \pi x)$ is $2$ and its period is $\dfrac{\pi }{2}$ .

False

True or False The graph of the sine function has infinitely many $x$ -intercepts.

True

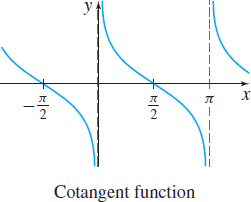
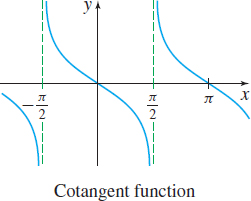
The graph of $y=\tan x$ is symmetric with respect to the _____.

Origin

The graph of $y=\sec x$ is symmetric with respect to the _____.

$y$ -axis

Explain, in your own words, what it means for a function to be periodic.

Answers will vary.

Practice Problems

In Problems 13–16, use the even-odd properties to find the exact value of each expression.

$\tan\! \left(\! -\dfrac{\pi }{4} \right)$

$-1$

$\sin\! \left(\!\! -\dfrac{3\pi }{2}\! \right)$

$\csc\! \left(\! -\dfrac{\pi }{3} \right)$

$-\frac{2\sqrt{3}}{3}$

$\cos\! \left(\! -\dfrac{\pi }{6} \right)$

In Problems 17–20, if necessary, refer to a graph to answer each question.

What is the $y$ -intercept of ${f}( x) =\tan x$ ?

$0$

Find the $x$ -intercepts of $f( x) =\sin x$ on the interval $[-2\pi ,2\pi]$ .

What is the smallest value of $f(x) =\cos x$ ?

$-1$

For what numbers $x$ , $-2\pi \leq x\leq 2\pi$ , does $\sin x=1$ ? Where in the interval $[ -2\pi ,2\pi]$ does $\sin x=-1$ ?

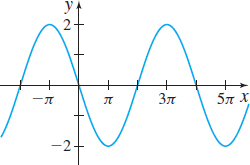
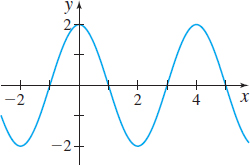
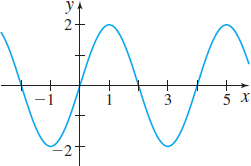
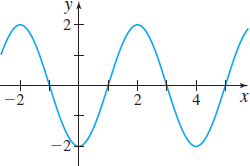
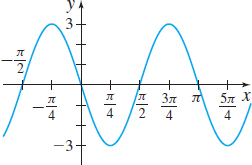
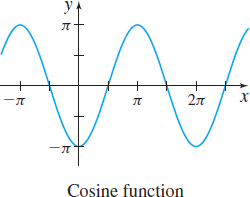
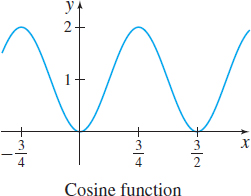
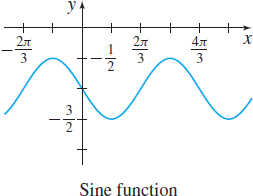
In Problems 21–26, the graphs of six trigonometric functions are given. Match each graph to one of the following functions:

$y=2\sin\! \left( \dfrac{\pi }{2}x\right)$
$y=2\cos\! \left( \dfrac{\pi }{2}x\right)$
$y=3\cos ( 2x)$
$y=-3\sin ( 2x)$
$y=-2\cos\! \left( \dfrac{\pi }{2}x\right)$
$y=-2\sin\! \left( \dfrac{1}{2}x\right)$

(f)

(a)

(d)

In Problems 27–32, graph each function using transformations. Be sure to label key points and show at least two periods.

$f( x) =4\sin (\pi x)$

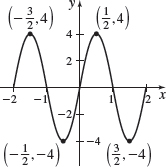
$f( x) =-3\cos x$

$f( x) =3\cos ( 2x) -4$

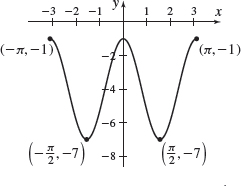
$f( x) =4\sin ( 2x) +2$

$f( x) =\tan\! \left( \dfrac{\pi }{2}x\! \right)$

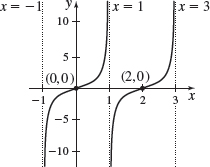
$f( x) =4\sec\! \left( \dfrac{1}{2}x\! \right)$

In Problems 33–36, determine the amplitude and period of each function.

$g( x) =\dfrac{1}{2}\cos ( \pi x)$

$\frac{1}{2}$ , $2$

$f( x) =\sin ( 2x)$

$g( x) =3\sin x$

$3$ , $2\pi$

$f( x) =-2\cos\! \left( \dfrac{3}{2}x\!\right)$

In Problems 37 and 38, write the sine function that has the given properties.

Amplitude: 2, Period: $\pi$

$f(x)=2\sin(2x)$

Amplitude: $\dfrac{1}{3}$ , Period: 2

In Problems 39 and 40, write the cosine function that has the given properties.

Amplitude: $\dfrac{1}{2}$ , Period: $\pi$

$f(x)=\frac{1}{2}\cos(2x)$

Amplitude: $3$ , Period: $4\pi$

In Problems 41–48, for each graph, find an equation involving the indicated trigonometric function.

$f(x) = -\sin\left(\frac{3}{2}x\right)$

$f(x) = 1-\cos\left(\frac{4\pi}{3}x\right)$

$f(x) = \cot x$

$f(x) = \tan\left(x-\frac{\pi}{2}\right)$

P.6 Assess Your UnderstandingPrinted Page 56

P.6 Assess Your Understanding
Printed Page 56