P.7 Inverse Trigonometric Functions
58
OBJECTIVES
When you finish this section, you should be able to:
- Define the inverse trigonometric functions (p. 58)
- Use the inverse trigonometric functions (p. 61)
- Solve trigonometric equations (p. 61)
We now investigate the inverse trigonometric functions. In calculus the inverses of the sine function, the tangent function, and the secant function are used most often. So we define these inverse functions first.
1 Define the Inverse Trigonometric Functions
Although the trigonometric functions are not one-to-one, we can restrict the domains of the trigonometric functions so that each new function will be one-to-one on its restricted domain. Then an inverse function can be defined on each restricted domain.
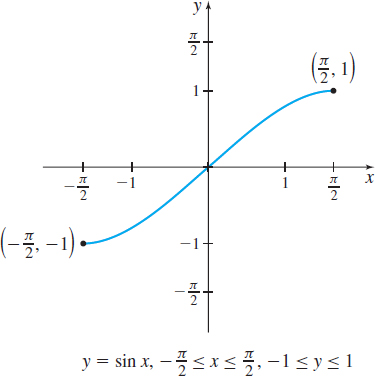
The Inverse Sine Function
If the domain of the function \(f( x) =\sin x\) is restricted to the interval \(\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right]\), the function \(y =\sin x\), \(-\dfrac{\pi }{2}\leq x\leq \dfrac{\pi }{2}\), is one-to-one and so has an inverse function. See Figure 82.
To obtain an equation for the inverse of \(y= \sin x\) on \(-\dfrac{\pi}{2}\leq x\leq \dfrac{\pi}{2}\), we interchange \(x\) and \(y\). Then the implicit form of the inverse is \(x=\sin y\), \(-\dfrac{\pi }{2}\leq y\leq \dfrac{\pi }{2}\). The explicit form of the inverse function is called the inverse sine of \(x\) and is written \(y= \sin ^{-1}x\).
IN WORDS
We read \(y=\sin ^{-1}{x}\) as "\({y}\) is the number (or angle) whose sine equals \(x\)".
spanDEFINITIONspan Inverse Sine Function
The inverse sine function, denoted by \(y= \sin ^{-1}x,\) or \(y=\arcsin x,\) is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\begin{array}{l} y = \sin ^{ - 1} \,x\,\quad{\rm{if}}\,{\rm{and}}\,{\rm{only}}\,{\rm{if}}\,\quad\,x = \sin \,y \\ \,\,\,\,\,\,{\rm{where}}\, - {\rm{1}} \le x \le 1\,\quad{\rm{and}}\,\quad - \frac{\pi }{2} \le y \le \frac{\pi }{2} \\ \end{array}}} \]

The domain of \(y =\sin ^{-1}x\) is the closed interval \( [ -1,1] \), and the range is the closed interval \(\left[ -\dfrac{ \pi }{2},\dfrac{\pi }{2}\right] \). The graph of \(y =\sin ^{-1}x\) is the reflection of the restricted portion of the graph of \( f( x) =\sin x\) about the line \(y=x.\) See Figure 83.
Because \(y=\sin x\) defined on the closed interval \(\left[ -\dfrac{\pi }{2}, \dfrac{\pi }{2}\right] \) and \(y=\sin ^{-1}x\) are inverse functions, \[\begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\begin{array}{l} \sin ^{ - 1} (\sin x) = x\,\quad{\rm{if}}\,x\,{\rm{is}}\,{\rm{in}}\,{\rm{the}}\,{\rm{closed}}\,{\rm{interval}}\,\,\left[ { - \frac{\pi }{{\rm{2}}},\frac{\pi }{2}} \right] \\ \end{array}}} \tag{1} \end{equation*} \] \[\begin{equation*}\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\begin{array}{l} \sin \,(\sin ^{ - 1} x) = x\,\quad{\rm{if}}\,x\,{\rm{is}}\,{\rm{in}}\,{\rm{the}}\,{\rm{closed}}\,{\rm{interval}}\,{\rm{[}} - {\rm{1,1]}} \\ \end{array}}} \tag{2} \end{equation*} \]
59
CAUTION
The superscript \(^{-1}\) that appears in \(y=\sin ^{-1}{x}\) is not an exponent but the symbol used to denote the inverse function. (To avoid confusion, \(y=\sin ^{-1}{x}\) is sometimes written \(y= {\rm arcsin}\ x\).)
Finding the Values of an Inverse Sine Function
Find the exact value of:
- \(\sin ^{-1}\dfrac{\sqrt{3}}{2}\)
- \(\sin ^{-1}\left( - \dfrac{\sqrt{2}}{2}\right)\)
- \(\sin ^{-1}\left( \sin \dfrac{ \pi }{8} \right)\)
- \(\sin ^{-1}\left( \sin \dfrac{5\pi }{8 } \right)\)
Solution (a) We seek an angle whose sine is \(\dfrac{\sqrt{3}}{2} .\) Since \(-1{<}\dfrac{\sqrt{3}}{2}{<}1,\) let \(y=\sin ^{-1}\dfrac{\sqrt{3}}{2}\). Then by definition, \(\sin y=\dfrac{\sqrt{3}}{2}\), where \(-\dfrac{\pi }{2} \leq y\leq \dfrac{\pi }{2}\). Although \(\sin y=\dfrac{\sqrt{3}}{2}\) has infinitely many solutions, the only number in the interval \(\left[ -\dfrac{ \pi }{2},\dfrac{\pi }{2}\right] \), for which \(\sin y=\dfrac{\sqrt{3}}{2}\), is \(\dfrac{\pi }{3}.\) So \(\sin ^{-1}\dfrac{\sqrt{3}}{2}=\dfrac{\pi }{3}\).
(b) We seek an angle whose sine is \(-\dfrac{\sqrt{2}}{2}.\) Since \( -1<-\dfrac{\sqrt{2}}{2}<1\), let \(y=\sin ^{-1}\left( -\dfrac{\sqrt{2}}{2}\right)\). Then by definition, \(\sin y=-\dfrac{\sqrt{2}}{2}\), where \(-\dfrac{\pi }{2}\leq y\leq \dfrac{\pi }{2}\). The only number in the interval \( \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right] ,\) whose sine is \(-\dfrac{ \sqrt{2}}{2},\) is \(-\dfrac{\pi }{4}\). So \(\sin ^{-1}\left( -\dfrac{\sqrt{2}}{ 2}\right) =-\dfrac{\pi }{4}\).
(c) Since the number \(\dfrac{\pi }{8}\) is in the interval \(\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right]\), we use (1). \[ \sin ^{-1}\left( \sin \dfrac{\pi }{8}\right) =\dfrac{\pi }{8} \]
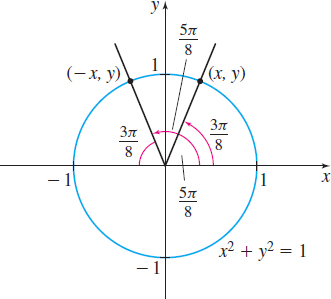
(d) Since the number \(\dfrac{5\pi }{8}\) is not in the closed interval \(\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right] ,\) we cannot use (1). Instead, we find a number \(x\) in the interval \(\left[ -\dfrac{\pi }{2} ,\dfrac{\pi }{2}\right] \) for which \(\sin x=\sin \dfrac{5\pi }{8}.\) Using Figure 84, we see that \(\sin \dfrac{5\pi }{8}=y=\sin \dfrac{3\pi }{8}.\) The number \(\dfrac{3\pi }{8}\) is in the interval \( \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2}\right]\), so \[ \sin ^{-1}\left( \sin \dfrac{5\pi }{8}\right) =\sin ^{-1}\left( \sin \dfrac{ 3\pi }{8}\right) =\dfrac{3\pi }{8} \]
NOW WORK
Problems 9 and 17.
The Inverse Tangent Function
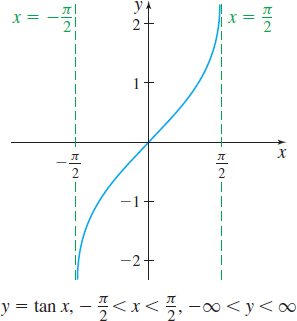
The tangent function \(y=\tan x\) is not one-to-one. To define the inverse tangent function, we restrict the domain of \(y =\tan x\) to the open interval \(\left( -\dfrac{\pi }{2},\dfrac{\pi }{2}\right)\). On this interval, \(y =\tan x\) is one-to-one. See Figure 85.
Now use the steps for finding the inverse of a one-to-one function:
Step 1 \(y=\tan x,\) \(-\dfrac{\pi }{2}<x<\dfrac{\pi }{2}\).
Step 2 Interchange \(x\) and \(y,\) to obtain \(x=\tan y\), \(-\dfrac{\pi }{2}<y< \dfrac{\pi }{2},\) the implicit form of the inverse tangent function.
Step 3 The explicit form is called the inverse tangent of \(x\), and is denoted by \(y= \tan ^{-1}x.\)
60
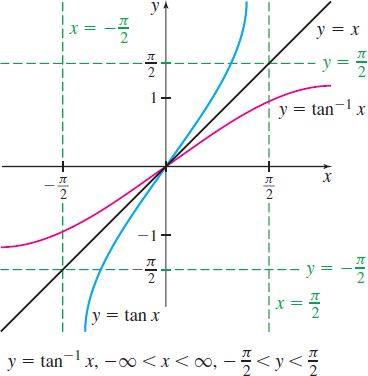
spanDEFINITIONspan Inverse Tangent Function
The inverse tangent function, symbolized by \( y= \tan ^{-1}x,\) or \(y=\arctan x,\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\begin{array}{l} \,\,\,\,\,\,\,\,\,y = \tan ^{ - 1} \,x\,\quad{\rm{if}}\,{\rm{and}}\,{\rm{only}}\,{\rm{if}}\,\quad\,x = \tan \,y \\ {\rm{where}}\, - \infty < x < \infty \,\quad{\rm{and}}\,\quad - \frac{\pi }{2} < y < \frac{\pi }{2} \\ \end{array}}} \]
The domain of the function \(y =\tan ^{-1}x\) is the set of all real numbers and its range is \(-\dfrac{\pi }{2}<y<\dfrac{\pi }{2}\). To graph \(y =\tan ^{-1}x,\) reflect the graph of \(y =\tan x\), \(-\dfrac{\pi}{2}<x<\dfrac{\pi}{2}\), about the line \(y=x\), as shown in Figure 86.
NOW WORK
Problem 13.
The Inverse Secant Function
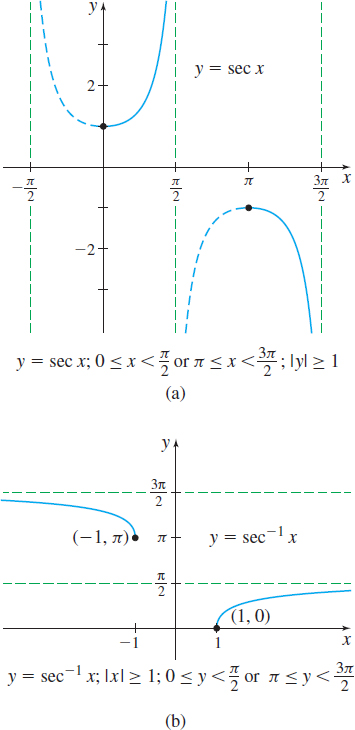
To define the inverse secant function, we restrict the domain of the function \(y =\sec x\) to the set \(\left[ 0,\dfrac{\pi }{2}\right) \cup \left[ \pi ,\dfrac{3\pi }{2}\right)\). See Figure 87(a). An equation for the inverse function is obtained by following the steps for finding the inverse of a one-to-one function. By interchanging \(x\) and \(y,\) we obtain the implicit form of the inverse function: \(x=\sec y\), where \(0\leq y<\dfrac{\pi }{2}\) or \(\pi \leq y< \dfrac{3\pi }{2}\). The explicit form is called the inverse secant of \(x\) and is written \(y= \sec ^{-1}x\). The graph of \(y=\sec^{-1}x\) is given in Figure 87(b).
spanDEFINITIONspan Inverse Secant Function
The inverse secant function, symbolized by \(y= \sec ^{-1}x\), or \(y\) = arcsec \(x\), is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\begin{array}{c} y= \sec ^{-1}x\quad \hbox{ if and only if }\quad x=\sec y \\[6pt] \hbox{where } \vert x\vert \geq 1\quad \hbox{and}\quad 0\leq y< \dfrac{\pi }{2}\quad \hbox{or}\quad \pi \leq y<\dfrac{3\pi }{2} \end{array}}} \]
You may wonder why we chose the restriction we did to define \(y=\sec ^{-1}x. \) The reason is that this restriction not only makes \(y=\sec x\) one-to-one, but it also makes \(\tan x\geq 0.\) With \(\tan x\geq 0,\) the derivative formula for the inverse secant function is simpler, as we will see in Chapter 3.
The remaining three inverse trigonometric functions are defined as follows.
spanDEFINITIONspan
- Inverse Cosine Function \(y= \cos ^{-1}x\) if and only if \(x=\cos y, {\rm{where}}\, -1\leq x\leq 1 \quad {\rm{and}}\, \quad 0\leq y\leq \pi \)
- Inverse Cotangent Function \(y=\cot ^{-1}x\) if and only if \(x=\cot y, {\rm{where}}\, -\infty <x<\infty \quad {\rm{and}}\, \quad 0<y<\pi \)
- Inverse Cosecant Function \(y=\csc ^{-1}x\) if and only if \(x=\csc y, {\rm{where}}\, \vert x\vert \geq 1\, {\rm{and}}\, \\ -\pi <y\leq - \dfrac{\pi }{2} \quad {\rm{or}} \quad 0<y\leq \dfrac{\pi }{2}\)
61
The following three identities involve the inverse trigonometric functions. The proofs may be found in books on trigonometry.
THEOREM
- \(\cos ^{-1}x=\dfrac{\pi }{2}-\sin ^{-1}x,\) \(-1\leq x\leq 1\)
- \(\cot ^{-1}x=\dfrac{\pi }{2}-\tan ^{-1}x\), \(-\infty <x<\infty \)
- \(\csc ^{-1}x= \dfrac{\pi }{2}-\sec ^{-1}x,\quad \vert x\vert \geq 1\)
The identities above are used whenever the inverse cosine, inverse cotangent, and inverse cosecant functions are needed. The graphs of the inverse cosine, inverse cotangent, and inverse cosecant functions can also be obtained by using these identities to transform the graphs of \(y=\sin^{-1} x,\) \( y=\tan^{-1} x\), and \(y=\sec^{-1} x\), respectively.
2 Use the Inverse Trigonometric Functions

Writing a Trigonometric Expression as an Algebraic Expression
Write \(\sin ( \tan ^{-1}u) \) as an algebraic expression containing \(u.\)
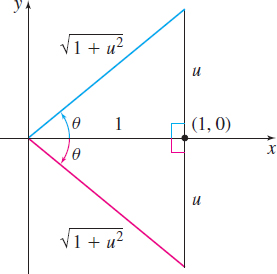
Solution Let \(\theta =\tan ^{-1}u\) so that \(\tan \theta =u\), where \(-\dfrac{\pi }{2}<\theta <\dfrac{\pi }{2}\). We note that in the interval \(\left( -\dfrac{\pi }{2},\dfrac{\pi }{2}\right) ,\) \(\sec \theta >0.\) Then \[ \begin{array}{l} \sin (\tan ^{ - 1} u) = \sin \theta = \sin \theta \cdot \frac{{\cos \theta }}{{\cos \theta }} = \tan \theta \cos \theta \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\tan \theta }}{{\sec \theta }} = \frac{{\tan \theta }}{{\sqrt {1 + \tan ^2 \theta } }} = \frac{u}{{\sqrt {1 + u^2 } }} \\ {\color{#0066A7}{ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\sec ^2 \theta = 1 + \mathop {\tan ^2 }\limits^ \uparrow \theta ;\sec \theta > 0}} \\ \end{array} \]
An alternate method of obtaining the solution to Example 2 uses right triangles. Let \(\theta =\tan ^{-1}u\) so that \(\tan \theta =u\), \(- \dfrac{\pi }{2}<\theta <\dfrac{\pi }{2}\), and label the right triangles drawn in Figure 88. Using the Pythagorean Theorem, the hypotenuse of each triangle is \(\sqrt{1+u^{2}}.\) Then \(\sin (\tan ^{-1}u) =\sin \theta =\dfrac{u}{\sqrt{1+u^{2}}}.\)
NOW WORK
Problem 23.
3 Solve Trigonometric Equations
Inverse trigonometric functions can be used to solve trigonometric equations.
Solving Trigonometric Equations
Solve the equations:
- \(\sin \theta =\dfrac{1}{2}\)
- \(\cos \theta =0.4\)
Give a general formula for all the solutions and list all the solutions in the interval \([ -2\pi ,2\pi ] .\)
62

Solution (a) Use the inverse sine function \(y =\sin ^{-1} x\), \(-\dfrac{\pi}{2}\leq y\leq \dfrac{\pi}{2}\). \[ \begin{array}{l} \sin \theta = \frac{1}{2} \\ \,\,\,\theta = \sin ^{ - 1} \frac{1}{2}\, \quad {\color{#0066A7}{- \frac{\pi }{2} \le \theta \le \frac{\pi }{2}}} \\ \,\,\theta = \frac{\pi }{6} \\ \end{array} \]
Over the interval \([ 0,2\pi ] ,\) there are two angles \(\theta \) for which \(\sin \theta =\dfrac{1}{2}\). See Figure 89.
All the solutions of \(\sin \theta =\dfrac{1}{2}\) are given by the general formula \[ \theta =\dfrac{\pi }{6}+2k\pi\quad {\rm \ or \ }\quad \theta =\dfrac{5\pi }{6}+2k\pi,\qquad {\rm where }\ k \ \hbox{is any integer} \]
The solutions in the interval \([-2\pi, 2\pi] \) are \[ \left\{ -\dfrac{11\pi }{6},-\dfrac{7\pi }{6},\dfrac{\pi }{6 },\dfrac{5\pi }{6}\right\} \]
(b) A calculator must be used to solve \(\cos \theta =0.4\). Then \[ \theta =\cos ^{-1}\left( 0.4\right) \approx 1.159279 \quad 0\leq \theta \leq \pi \]
Rounded to three decimal places, \(\theta \,{=}\,\cos ^{-1}0.4=1.159\) radians. But there is another angle \(\theta \) in the interval \([ 0,2\pi ] \) for which \(\cos \theta =0.4\), namely, \(\theta \approx 2\pi -1.159\) \(\approx 5.124\) radians.
Because the cosine function has period \(2\pi \), all the solutions of \(\cos \theta =0.4\) are given by the general formulas \[ \theta \approx 1.159+2k\pi \quad \hbox{or} \quad \theta \approx 5.124+2k\pi,\qquad \hbox{ where } k \hbox{ is any integer} \]
The solutions in the interval \([ -2\pi ,2\pi ] \) are \(\left\{ -5.124,-1.159, 1.159, 5.124\right\}\).
NOW WORK
Problem 45.
Solving a Trigonometric Equation
Solve the equation \(\sin ( 2\theta ) =\dfrac{1}{2}\), where \(0\leq \theta <2\pi\).
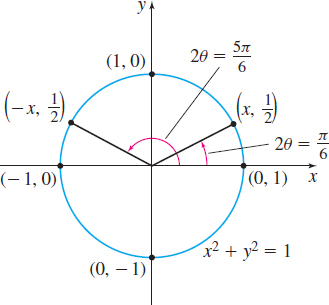
Solution In the interval \(\left[ 0,2\pi \right) \), the sine function has the value \(\dfrac{1}{2}\) at \(\theta =\dfrac{\pi }{6}\) and at \( \theta = \dfrac{5\pi }{6}\) as shown in Figure 90. Since the period of the sine function is \({2\pi }\) and the argument in the equation \(\sin ( 2\theta ) =\dfrac{1}{2} \) is \(2\theta\), we write the general formula for all the solutions. \[ \begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 2\theta =\dfrac{\pi }{6}+2k\pi & {\rm or} & 2\theta =\dfrac{5\pi }{6}+2k\pi, & & \hbox{ where }k \hbox{ is any integer} \\ \theta =\dfrac{\pi }{12}+k\pi & & \theta =\dfrac{5\pi }{12}+k\pi & & \end{array} \]
The solutions of \(\sin ( 2\theta ) =\dfrac{1}{2},\) \(0\leq \theta <2\pi \), are \(\left\{ \dfrac{\pi }{12}, \dfrac{5\pi }{12}, \dfrac{13\pi }{12} , \dfrac{17\pi }{12}\right\} .\)
NOW WORK
Problem 31.
63
Many trigonometric equations can be solved by applying algebra techniques such as factoring or using the quadratic formula. It is often necessary to begin by using a trigonometric identity to express the given equation in a familiar form.
NEED TO REVIEW?
Trigonometric identities are discussed in Appendix Section A.4, pp. A-32 to A-35.
Solving a Trigonometric Equation
Solve the equation \(3\sin \theta -\cos ^{2}\theta =3\), where \(0\leq \theta <2\pi \).
Solution The equation involves both sine and cosine functions. We use the Pythagorean identity \(\sin ^{2}\theta +\cos ^{2}\theta =1\) to rewrite the equation in terms of \(\sin \theta .\) \[ \begin{eqnarray*} 3\sin \theta -\cos ^{2}\theta &=&3 \\ 3\sin \theta -( 1-\sin ^{2}\theta)~&=&3\qquad {\color{#0066A7}{\cos ^{2}{\theta =1-}\sin ^{2}{\theta }}} \\ \sin ^{2}\theta +3\sin \theta -4 &=&0 \end{eqnarray*} \]
This is a quadratic equation in \(\sin \theta\). Factor the left side and solve for \(\sin \theta .\) \[ \begin{array}{rcl@{\quad}c@{\quad}rcl} ( \sin \theta +4) (\sin \theta -1)~&=&0& \\ \sin \theta +4 &=&0&\hbox{ or }& \sin \theta -1&=&0 \\ \sin \theta &=&-4&\hbox{ or }& \sin \theta &=&1 \end{array} \]
The range of the sine function is \(-1\leq y\leq 1,\) so \(\sin \theta =-4\) has no solution. Solving \(\sin \theta =1,\) we obtain \[ \theta =\sin ^{-1}1=\dfrac{\pi }{2} \]
The only solution in the interval \(\left[ 0,2\pi \right) \) is \(\dfrac{\pi }{2 }.\)
NOW WORK
Problem 35.